Question-60717

Question Number 60717 by peter frank last updated on 24/May/19

Commented by Prithwish sen last updated on 25/May/19

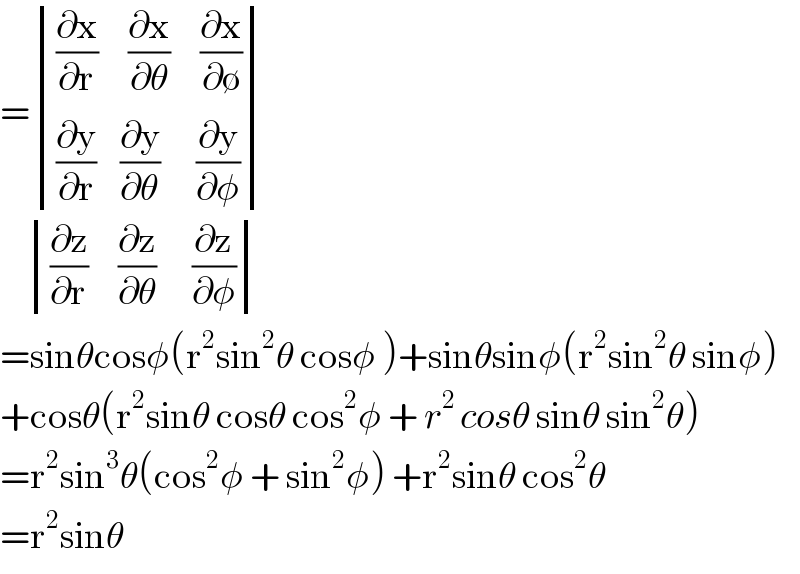
= determinant ((((∂x/∂r) (∂x/∂θ) (∂x/∂∅))),(((∂y/∂r) (∂y/∂θ) (∂y/∂φ)))) determinant ((((∂z/∂r) (∂z/∂θ) (∂z/∂φ)))) =sinθcosφ(r^2 sin^2 θ cosφ )+sinθsinφ(r^2 sin^2 θ sinφ) +cosθ(r^2 sinθ cosθ cos^2 φ + r^(2 ) cosθ sinθ sin^2 θ) =r^2 sin^3 θ(cos^2 φ + sin^2 φ) +r^2 sinθ cos^2 θ =r^2 sinθ

$$=\begin{vmatrix}{\frac{\partial\mathrm{x}}{\partial\mathrm{r}}\:\:\:\:\:\frac{\partial\mathrm{x}}{\partial\theta}\:\:\:\:\:\frac{\partial\mathrm{x}}{\partial\emptyset}}\\{\frac{\partial\mathrm{y}}{\partial\mathrm{r}}\:\:\:\:\frac{\partial\mathrm{y}}{\partial\theta}\:\:\:\:\:\:\frac{\partial\mathrm{y}}{\partial\phi}}\end{vmatrix} \\ $$$$\:\:\:\:\begin{vmatrix}{\frac{\partial\mathrm{z}}{\partial\mathrm{r}}\:\:\:\:\:\frac{\partial\mathrm{z}}{\partial\theta}\:\:\:\:\:\:\frac{\partial\mathrm{z}}{\partial\phi}}\end{vmatrix} \\ $$$$=\mathrm{sin}\theta\mathrm{cos}\phi\left(\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\:\mathrm{cos}\phi\:\right)+\mathrm{sin}\theta\mathrm{sin}\phi\left(\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\:\mathrm{sin}\phi\right) \\ $$$$+\mathrm{cos}\theta\left(\mathrm{r}^{\mathrm{2}} \mathrm{sin}\theta\:\mathrm{cos}\theta\:\mathrm{cos}^{\mathrm{2}} \phi\:+\:{r}^{\mathrm{2}\:} {cos}\theta\:\mathrm{sin}\theta\:\mathrm{sin}^{\mathrm{2}} \theta\right) \\ $$$$=\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{3}} \theta\left(\mathrm{cos}^{\mathrm{2}} \phi\:+\:\mathrm{sin}^{\mathrm{2}} \phi\right)\:+\mathrm{r}^{\mathrm{2}} \mathrm{sin}\theta\:\mathrm{cos}^{\mathrm{2}} \theta \\ $$$$=\mathrm{r}^{\mathrm{2}} \mathrm{sin}\theta \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply