Question-60745

Question Number 60745 by Tawa1 last updated on 25/May/19

Commented by Prithwish sen last updated on 25/May/19

(([(n+1)!]^n )/((n!)^(n+1) )) =[(((n+1)!)/(n!))]^n .(1/(n!)) =(((n+1)^n )/(n!)) =(((n+1))/1).(((n+1))/2)............(((n+1))/n) >1 ∴ [(n+1)!]^n >(n!)^(n+1) i.e( 101!)^(100) is the larger

$$\frac{\left[\left(\mathrm{n}+\mathrm{1}\right)!\right]^{\mathrm{n}} }{\left(\mathrm{n}!\right)^{\mathrm{n}+\mathrm{1}} }\:=\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)!}{\mathrm{n}!}\right]^{\mathrm{n}} .\frac{\mathrm{1}}{\mathrm{n}!}\:=\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{1}}.\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}…………\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{n}}\:>\mathrm{1} \\ $$$$\therefore\:\left[\left(\mathrm{n}+\mathrm{1}\right)!\right]^{\mathrm{n}} \:>\left(\mathrm{n}!\right)^{\mathrm{n}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{i}.\mathrm{e}\left(\:\mathrm{101}!\right)^{\mathrm{100}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{larger} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by maxmathsup by imad last updated on 25/May/19

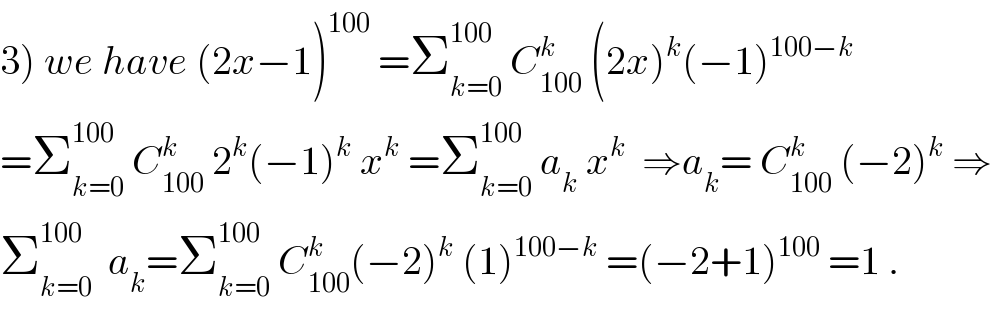
3) we have (2x−1)^(100) =Σ_(k=0) ^(100) C_(100) ^k (2x)^k (−1)^(100−k) =Σ_(k=0) ^(100) C_(100) ^k 2^k (−1)^k x^k =Σ_(k=0) ^(100) a_k x^k ⇒a_k = C_(100) ^k (−2)^k ⇒ Σ_(k=0) ^(100) a_k =Σ_(k=0) ^(100) C_(100) ^k (−2)^k (1)^(100−k) =(−2+1)^(100) =1 .

$$\left.\mathrm{3}\right)\:{we}\:{have}\:\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{100}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:{C}_{\mathrm{100}} ^{{k}} \:\left(\mathrm{2}{x}\right)^{{k}} \left(−\mathrm{1}\right)^{\mathrm{100}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:{C}_{\mathrm{100}} ^{{k}} \:\mathrm{2}^{{k}} \left(−\mathrm{1}\right)^{{k}} \:{x}^{{k}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:{a}_{{k}} \:{x}^{{k}} \:\:\Rightarrow{a}_{{k}} =\:{C}_{\mathrm{100}} ^{{k}} \:\left(−\mathrm{2}\right)^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:\:{a}_{{k}} =\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:{C}_{\mathrm{100}} ^{{k}} \left(−\mathrm{2}\right)^{{k}} \:\left(\mathrm{1}\right)^{\mathrm{100}−{k}} \:=\left(−\mathrm{2}+\mathrm{1}\right)^{\mathrm{100}} \:=\mathrm{1}\:. \\ $$

Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by maxmathsup by imad last updated on 25/May/19

$${you}\:{are}\:{welcome}\:{sir}\:. \\ $$

Answered by tanmay last updated on 25/May/19

2)(2y−x)^k =(2y)^k −kc_1 (2y)^(k−1) (x)+kc_2 (2y)^(k−2) (x)^2 −kc_3 (2y)^(k−3) x^3 +...(−1)^k (x)^k so sum of coefficients =2^k −kc_1 (2)^(k−1) +kc_2 2^(k−2) −kc_3 2^(k−3) +..+(−1)^k =(2×1−1)^k [put x=1 and y=1] =1

$$\left.\mathrm{2}\right)\left(\mathrm{2}{y}−{x}\right)^{{k}} =\left(\mathrm{2}{y}\right)^{{k}} −{kc}_{\mathrm{1}} \left(\mathrm{2}{y}\right)^{{k}−\mathrm{1}} \left({x}\right)+{kc}_{\mathrm{2}} \left(\mathrm{2}{y}\right)^{{k}−\mathrm{2}} \left({x}\right)^{\mathrm{2}} −{kc}_{\mathrm{3}} \left(\mathrm{2}{y}\right)^{{k}−\mathrm{3}} {x}^{\mathrm{3}} +…\left(−\mathrm{1}\right)^{{k}} \left({x}\right)^{{k}} \\ $$$${so}\:{sum}\:{of}\:{coefficients} \\ $$$$=\mathrm{2}^{{k}} −{kc}_{\mathrm{1}} \left(\mathrm{2}\right)^{{k}−\mathrm{1}} +{kc}_{\mathrm{2}} \mathrm{2}^{{k}−\mathrm{2}} −{kc}_{\mathrm{3}} \mathrm{2}^{{k}−\mathrm{3}} +..+\left(−\mathrm{1}\right)^{{k}} \\ $$$$=\left(\mathrm{2}×\mathrm{1}−\mathrm{1}\right)^{{k}} \:\:\:\left[{put}\:{x}=\mathrm{1}\:\:{and}\:\:{y}=\mathrm{1}\right] \\ $$$$=\mathrm{1}\:\:\: \\ $$$$ \\ $$

Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay last updated on 25/May/19

3)(2x−1)^(100) =a_0 +a_1 x+...+a_(100) x^(100) now put x=1 (1)^(100) =1=sum of coefficient

$$\left.\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{100}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+…+{a}_{\mathrm{100}} {x}^{\mathrm{100}} \\ $$$${now}\:{put}\:{x}=\mathrm{1} \\ $$$$\left(\mathrm{1}\right)^{\mathrm{100}} =\mathrm{1}={sum}\:{of}\:{coefficient} \\ $$

Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay last updated on 25/May/19

3) ii)(x^3 −x−1)^(99) =a_0 +a_1 x+a_2 x^2 +...+a_i x^(297) put x=1 sum of coefficient=(1^3 −1−1)^(99) =−1

$$\left.\mathrm{3}\right) \\ $$$$\left.{ii}\right)\left({x}^{\mathrm{3}} −{x}−\mathrm{1}\right)^{\mathrm{99}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +…+{a}_{{i}} {x}^{\mathrm{297}} \\ $$$${put}\:{x}=\mathrm{1}\: \\ $$$${sum}\:{of}\:{coefficient}=\left(\mathrm{1}^{\mathrm{3}} −\mathrm{1}−\mathrm{1}\right)^{\mathrm{99}} =−\mathrm{1} \\ $$

Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay last updated on 25/May/19

4) (2x+3y−z)^(20) put y=1 z=2 (2x+1)^(20) =a_0 x^(20) +a_1 x^(19) +a_2 x^(18) +...+1 now put y=−1 z=−2 (2x−1)^(20) =a_0 x^(20) −a_1 x^(19) +a_2 x^(18) +...+1 (2x+1)^(20) −(2x−1)^(20) =2[a_1 x^(19) +a_3 x^(17) +...] put x=1 both side so sum of coefficient containing odd power of x is =((3^(20) −1^(20) )/2) =((3^(20) −1)/2)

$$\left.\mathrm{4}\right) \\ $$$$\left(\mathrm{2}{x}+\mathrm{3}{y}−{z}\right)^{\mathrm{20}} \\ $$$${put}\:{y}=\mathrm{1}\:{z}=\mathrm{2} \\ $$$$\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{20}} ={a}_{\mathrm{0}} {x}^{\mathrm{20}} +{a}_{\mathrm{1}} {x}^{\mathrm{19}} +{a}_{\mathrm{2}} {x}^{\mathrm{18}} +…+\mathrm{1} \\ $$$${now}\:{put}\:{y}=−\mathrm{1}\:\:{z}=−\mathrm{2} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{20}} ={a}_{\mathrm{0}} {x}^{\mathrm{20}} −{a}_{\mathrm{1}} {x}^{\mathrm{19}} +{a}_{\mathrm{2}} {x}^{\mathrm{18}} +…+\mathrm{1} \\ $$$$\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{20}} −\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{20}} \\ $$$$=\mathrm{2}\left[{a}_{\mathrm{1}} {x}^{\mathrm{19}} +{a}_{\mathrm{3}} {x}^{\mathrm{17}} +…\right] \\ $$$${put}\:{x}=\mathrm{1}\:{both}\:{side} \\ $$$${so}\:{sum}\:{of}\:{coefficient}\:{containing}\:{odd}\:{power}\:{of} \\ $$$${x}\:{is} \\ $$$$=\frac{\mathrm{3}^{\mathrm{20}} −\mathrm{1}^{\mathrm{20}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}^{\mathrm{20}} −\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Prithwish sen last updated on 25/May/19