Question-60748

Facebook Tweet Pin

Question Number 60748 by ajfour last updated on 25/May/19

Commented by ajfour last updated on 25/May/19

$${Determine}\:{r}\left(\theta\right). \\ $$

Answered by ajfour last updated on 25/May/19

Commented by ajfour last updated on 05/Jun/19

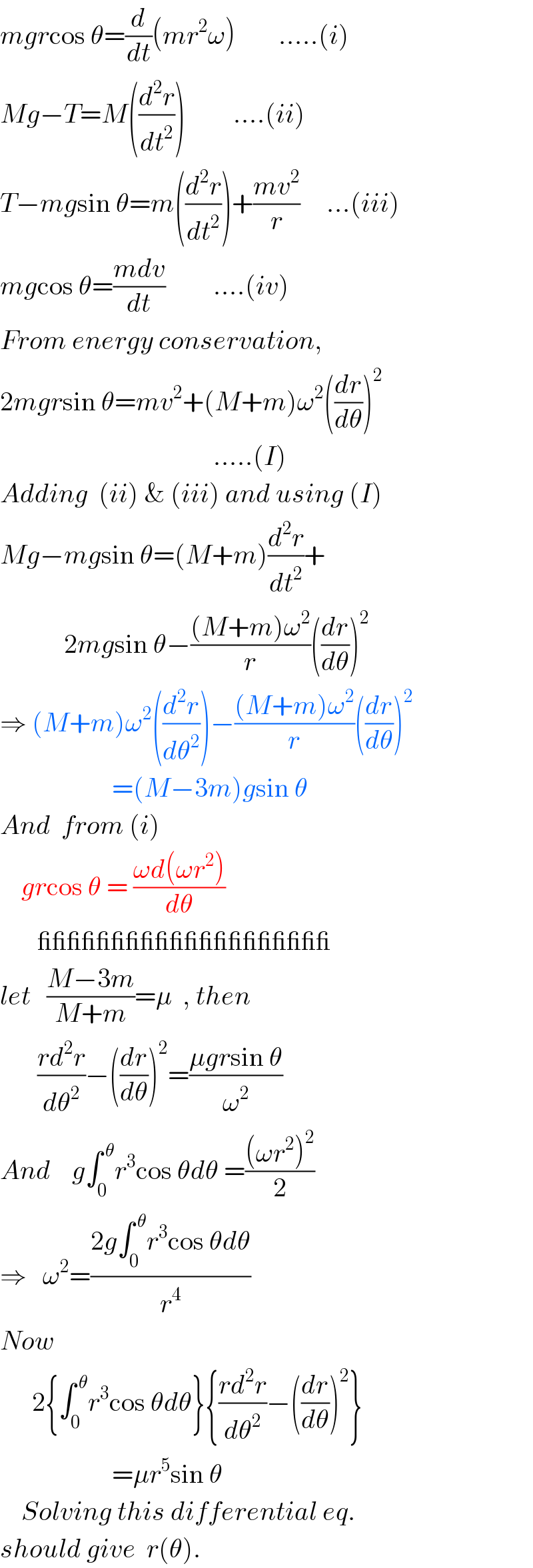
mgrcos θ=(d/dt)(mr^2 ω) .....(i) Mg−T=M((d^2 r/dt^2 )) ....(ii) T−mgsin θ=m((d^2 r/dt^2 ))+((mv^2 )/r) ...(iii) mgcos θ=((mdv)/dt) ....(iv) From energy conservation, 2mgrsin θ=mv^2 +(M+m)ω^2 ((dr/dθ))^2 .....(I) Adding (ii) & (iii) and using (I) Mg−mgsin θ=(M+m)(d^2 r/dt^2 )+ 2mgsin θ−(((M+m)ω^2 )/r)((dr/dθ))^2 ⇒ (M+m)ω^2 ((d^2 r/dθ^2 ))−(((M+m)ω^2 )/r)((dr/dθ))^2 =(M−3m)gsin θ And from (i) grcos θ = ((ωd(ωr^2 ))/dθ) ____________________ let ((M−3m)/(M+m))=μ , then ((rd^2 r)/dθ^2 )−((dr/dθ))^2 =((μgrsin θ)/ω^2 ) And g∫_0 ^( θ) r^3 cos θdθ =(((ωr^2 )^2 )/2) ⇒ ω^2 =((2g∫_0 ^( θ) r^3 cos θdθ)/r^4 ) Now 2{∫_0 ^( θ) r^3 cos θdθ}{((rd^2 r)/dθ^2 )−((dr/dθ))^2 } =μr^5 sin θ Solving this differential eq. should give r(θ).

$${mgr}\mathrm{cos}\:\theta=\frac{{d}}{{dt}}\left({mr}^{\mathrm{2}} \omega\right)\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$${Mg}−{T}={M}\left(\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }\right)\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${T}−{mg}\mathrm{sin}\:\theta={m}\left(\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }\right)+\frac{{mv}^{\mathrm{2}} }{{r}}\:\:\:\:\:…\left({iii}\right) \\ $$$${mg}\mathrm{cos}\:\theta=\frac{{mdv}}{{dt}}\:\:\:\:\:\:\:\:\:….\left({iv}\right) \\ $$$${From}\:{energy}\:{conservation}, \\ $$$$\mathrm{2}{mgr}\mathrm{sin}\:\theta={mv}^{\mathrm{2}} +\left({M}+{m}\right)\omega^{\mathrm{2}} \left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({I}\right) \\ $$$${Adding}\:\:\left({ii}\right)\:\&\:\left({iii}\right)\:{and}\:{using}\:\left({I}\right) \\ $$$${Mg}−{mg}\mathrm{sin}\:\theta=\left({M}+{m}\right)\frac{{d}^{\mathrm{2}} {r}}{{dt}^{\mathrm{2}} }+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{mg}\mathrm{sin}\:\theta−\frac{\left({M}+{m}\right)\omega^{\mathrm{2}} }{{r}}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left({M}+{m}\right)\omega^{\mathrm{2}} \left(\frac{{d}^{\mathrm{2}} {r}}{{d}\theta^{\mathrm{2}} }\right)−\frac{\left({M}+{m}\right)\omega^{\mathrm{2}} }{{r}}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({M}−\mathrm{3}{m}\right){g}\mathrm{sin}\:\theta \\ $$$${And}\:\:{from}\:\left({i}\right) \\ $$$$\:\:\:\:{gr}\mathrm{cos}\:\theta\:=\:\frac{\omega{d}\left(\omega{r}^{\mathrm{2}} \right)}{{d}\theta} \\ $$$$\:\:\:\:\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${let}\:\:\:\frac{{M}−\mathrm{3}{m}}{{M}+{m}}=\mu\:\:,\:{then} \\ $$$$\:\:\:\:\:\:\:\frac{{rd}^{\mathrm{2}} {r}}{{d}\theta^{\mathrm{2}} }−\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} =\frac{\mu{gr}\mathrm{sin}\:\theta}{\omega^{\mathrm{2}} } \\ $$$${And}\:\:\:\:{g}\int_{\mathrm{0}} ^{\:\theta} {r}^{\mathrm{3}} \mathrm{cos}\:\theta{d}\theta\:=\frac{\left(\omega{r}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}\int_{\mathrm{0}} ^{\:\theta} {r}^{\mathrm{3}} \mathrm{cos}\:\theta{d}\theta}{{r}^{\mathrm{4}} } \\ $$$${Now} \\ $$$$\:\:\:\:\:\:\mathrm{2}\left\{\int_{\mathrm{0}} ^{\:\theta} {r}^{\mathrm{3}} \mathrm{cos}\:\theta{d}\theta\right\}\left\{\frac{{rd}^{\mathrm{2}} {r}}{{d}\theta^{\mathrm{2}} }−\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mu{r}^{\mathrm{5}} \mathrm{sin}\:\theta \\ $$$$\:\:\:\:{Solving}\:{this}\:{differential}\:{eq}. \\ $$$${should}\:{give}\:\:{r}\left(\theta\right).\: \\ $$

Commented by mr W last updated on 26/May/19

$${really}\:{not}\:{easy}\:{question}\:{sir}! \\ $$$${i}'{m}\:{not}\:{sure}\:{if}\:{the}\:{system}\:{has}\:{an} \\ $$$${unique}\:{defined}\:{motion}… \\ $$

Commented by ajfour last updated on 26/May/19