Question Number 60873 by Kunal12588 last updated on 26/May/19
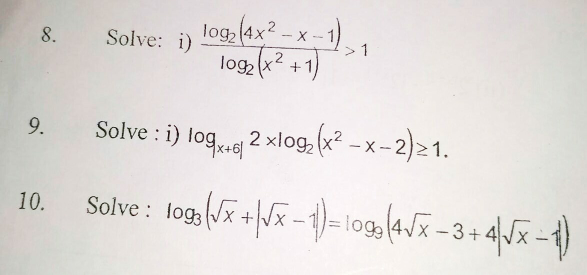
Commented by Prithwish sen last updated on 26/May/19
$$\left.\mathrm{i}\right)\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)−\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\:>\mathrm{0} \\ $$$$\frac{\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:>\mathrm{1} \\ $$$$\mathrm{3x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\:>\mathrm{0} \\ $$$$\left(\mathrm{3x}+\mathrm{2}\right)\left(\mathrm{x}−\mathrm{1}\right)>\mathrm{0} \\ $$$$\mathrm{either}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{or} \\ $$$$\mathrm{3x}+\mathrm{2}\:>\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}+\mathrm{2}<\mathrm{0} \\ $$$$\mathrm{x}−\mathrm{1}\:>\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:\mathrm{x}−\mathrm{1}\:<\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}>\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}<\:−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{the}\:\mathrm{soln}.\:\mathrm{is}\: \\ $$$$\mathrm{1}<\mathrm{x}<−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 27/May/19
![8) let D the set of definition x∈D ⇔4x^2 −x−1>0 Δ =1−4(−1) =5 ⇒x_1 =((1+(√5))/8) and x_2 =((1−(√5))/8) so D =]−∞,((1−(√5))/8)[∪]((1+(√5))/8),+∞[ (e) ⇔ ((ln(4x^2 −x−1))/(ln(x^2 +1))) >1 ⇒ln(4x^2 −x−1)>ln(x^2 +1) ⇒ 4x^2 −x−1>x^2 +1 ⇒3x^2 −x−2>0 →Δ =1−4(−6) =25 ⇒ x_1 =((1+5)/6) =1 and x_2 =((1−5)/6) =−(2/3) ⇒ S =(]−∞,−(2/3)[∪]1,+∞[)∩(]−∞,((1−(√5))/8)[∪]((1+(√5))/8) ,+∞[) =....](https://www.tinkutara.com/question/Q60902.png)
$$\left.\mathrm{8}\right)\:{let}\:{D}\:{the}\:{set}\:{of}\:{definition}\:\:\:{x}\in{D}\:\Leftrightarrow\mathrm{4}{x}^{\mathrm{2}} −{x}−\mathrm{1}>\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{1}\right)\:=\mathrm{5}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{8}}\:\:\:{and}\:\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\left.{so}\:{D}\:=\right]−\infty,\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{8}}\left[\cup\right]\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{8}},+\infty\left[\right. \\ $$$$\left({e}\right)\:\:\Leftrightarrow\:\frac{{ln}\left(\mathrm{4}{x}^{\mathrm{2}} −{x}−\mathrm{1}\right)}{{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:>\mathrm{1}\:\Rightarrow{ln}\left(\mathrm{4}{x}^{\mathrm{2}} −{x}−\mathrm{1}\right)>{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −{x}−\mathrm{1}>{x}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow\mathrm{3}{x}^{\mathrm{2}} −{x}−\mathrm{2}>\mathrm{0}\:\rightarrow\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{6}\right)\:=\mathrm{25}\:\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{5}}{\mathrm{6}}\:=\mathrm{1}\:\:{and}\:\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{5}}{\mathrm{6}}\:=−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$${S}\:=\left(\right]−\infty,−\frac{\mathrm{2}}{\mathrm{3}}\left[\cup\right]\mathrm{1},+\infty\left[\right)\cap\left(\right]−\infty,\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{8}}\left[\cup\right]\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{8}}\:,+\infty\left[\right)\:=…. \\ $$
Commented by Rasheed.Sindhi last updated on 27/May/19
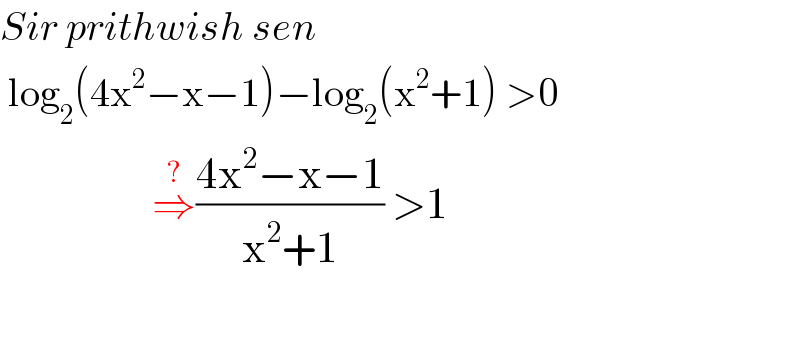
$${Sir}\:{prithwish}\:{sen} \\ $$$$\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)−\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{?} {\Rightarrow}\frac{\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:>\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Prithwish sen last updated on 27/May/19
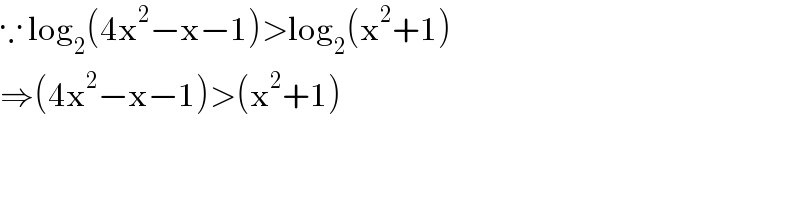
$$\because\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)>\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)>\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$
Commented by Kunal12588 last updated on 28/May/19
![well the answers are 8. x∈ (−∞,((−14)/3))∪(4,∞) 9. I don′t know 10. x∈ {4}∪ [0,1]](https://www.tinkutara.com/question/Q60978.png)
$${well}\:{the}\:{answers}\:{are}\: \\ $$$$\mathrm{8}.\:\:{x}\in\:\left(−\infty,\frac{−\mathrm{14}}{\mathrm{3}}\right)\cup\left(\mathrm{4},\infty\right) \\ $$$$\mathrm{9}.\:{I}\:{don}'{t}\:{know} \\ $$$$\mathrm{10}.\:\:{x}\in\:\left\{\mathrm{4}\right\}\cup\:\left[\mathrm{0},\mathrm{1}\right] \\ $$
Answered by tanmay last updated on 27/May/19
![9)log_a 2×log_2 b≥1 ((log2)/(loga))×((logb)/(log2))≥1 [log_a b when b>0 and a>0] logb≥loga b≥a (x^2 −x−2)≥∣6x∣ now (x^2 −x−2)>0 (x+1)(x−2)>0 f(x)=(x+1)(x−2) when x>2 f(x)>0 when x<−1 f(x)>0 when 2>x>−1 f(x)<0 so x ∉ (−1,2) ∣6x∣>0 so value of x can not lie between −1 and 2 solve x^2 −x−2≥∣6x∣ x^2 −x−2−∣6x∣≥0 when x>2 x^2 −x−2−6x≥0 x^2 −7x−2≥0 x=((7+(√(49+4×1×2)))/2)=7.275 when x<−1 x^2 −x−2+6x≥0 x^2 +5x−2≥0 x=((−5−(√(25+8)))/2)=−5.372](https://www.tinkutara.com/question/Q60933.png)
$$\left.\mathrm{9}\right){log}_{{a}} \mathrm{2}×{log}_{\mathrm{2}} {b}\geqslant\mathrm{1} \\ $$$$\frac{{log}\mathrm{2}}{{loga}}×\frac{{logb}}{{log}\mathrm{2}}\geqslant\mathrm{1}\:\:\:\:\left[\boldsymbol{{log}}_{\boldsymbol{{a}}} \boldsymbol{{b}}\:\:\:\:\boldsymbol{{when}}\:\boldsymbol{{b}}>\mathrm{0}\:\:\:\boldsymbol{{and}}\:\:\:\boldsymbol{{a}}>\mathrm{0}\right] \\ $$$${logb}\geqslant{loga} \\ $$$${b}\geqslant{a} \\ $$$$\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)\geqslant\mid\mathrm{6}{x}\mid \\ $$$$ \\ $$$${now}\:\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)>\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)>\mathrm{0} \\ $$$${f}\left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right) \\ $$$${when}\:{x}>\mathrm{2}\:\:\:\:\:\:\:{f}\left({x}\right)>\mathrm{0} \\ $$$${when}\:{x}<−\mathrm{1}\:\:\:{f}\left({x}\right)>\mathrm{0} \\ $$$${when}\:\:\mathrm{2}>{x}>−\mathrm{1}\:\:{f}\left({x}\right)<\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{x}}\:\notin\:\left(−\mathrm{1},\mathrm{2}\right) \\ $$$$\mid\mathrm{6}{x}\mid>\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{x}}\:\boldsymbol{{can}}\:\boldsymbol{{not}}\:\boldsymbol{{lie}}\:\boldsymbol{{between}}\:−\mathrm{1}\:\boldsymbol{{and}}\:\mathrm{2} \\ $$$${solve} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}\geqslant\mid\mathrm{6}{x}\mid \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}−\mid\mathrm{6}{x}\mid\geqslant\mathrm{0} \\ $$$${when}\:{x}>\mathrm{2} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}−\mathrm{6}{x}\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{2}\geqslant\mathrm{0} \\ $$$${x}=\frac{\mathrm{7}+\sqrt{\mathrm{49}+\mathrm{4}×\mathrm{1}×\mathrm{2}}}{\mathrm{2}}=\mathrm{7}.\mathrm{275}\: \\ $$$${when}\:{x}<−\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}+\mathrm{6}{x}\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2}\geqslant\mathrm{0} \\ $$$${x}=\frac{−\mathrm{5}−\sqrt{\mathrm{25}+\mathrm{8}}}{\mathrm{2}}=−\mathrm{5}.\mathrm{372} \\ $$$$ \\ $$
Answered by tanmay last updated on 27/May/19
![10)log_3 a =log_9 b [a>0 b>0] ((loga)/(log3))=((logb)/(log9)) ((loga)/(log3))=((logb)/(2log3)) loga^2 =logb a^2 =b ((√x) +∣(√x) −1∣)^2 =4(√x) −3+4∣(√x) −1∣ p=(√x) q=∣(√x) −1∣ (p+q)^2 =4p−3+4q (p+q)^2 −4(p+q)+3=0 (p+q−3)(p+q−1)=0 p+q=3 and p+q=1 (√x) +∣(√x) −1∣=3 so x=4 ( when ((√x)−1)>0 x>1) but when (√x) −1<0 x<1 then (√x) +∣(√x) −1∣ =(√x) −(√x) +1 =1 when x<1 so x=4 is the solution](https://www.tinkutara.com/question/Q60936.png)
$$\left.\mathrm{10}\right){log}_{\mathrm{3}} {a}\:={log}_{\mathrm{9}} {b}\:\:\:\left[{a}>\mathrm{0}\:\:\:\:{b}>\mathrm{0}\right] \\ $$$$\frac{{loga}}{{log}\mathrm{3}}=\frac{{logb}}{{log}\mathrm{9}} \\ $$$$\frac{{loga}}{{log}\mathrm{3}}=\frac{{logb}}{\mathrm{2}{log}\mathrm{3}} \\ $$$${loga}^{\mathrm{2}} ={logb} \\ $$$${a}^{\mathrm{2}} ={b} \\ $$$$\left(\sqrt{{x}}\:+\mid\sqrt{{x}}\:−\mathrm{1}\mid\right)^{\mathrm{2}} =\mathrm{4}\sqrt{{x}}\:−\mathrm{3}+\mathrm{4}\mid\sqrt{{x}}\:−\mathrm{1}\mid \\ $$$${p}=\sqrt{{x}}\:\:\:{q}=\mid\sqrt{{x}}\:−\mathrm{1}\mid \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} =\mathrm{4}{p}−\mathrm{3}+\mathrm{4}{q} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{4}\left({p}+{q}\right)+\mathrm{3}=\mathrm{0} \\ $$$$\left({p}+{q}−\mathrm{3}\right)\left({p}+{q}−\mathrm{1}\right)=\mathrm{0} \\ $$$${p}+{q}=\mathrm{3}\:\:\:{and}\:\:{p}+{q}=\mathrm{1} \\ $$$$\sqrt{{x}}\:+\mid\sqrt{{x}}\:−\mathrm{1}\mid=\mathrm{3}\:\:\boldsymbol{{so}}\:\boldsymbol{{x}}=\mathrm{4}\:\left(\:\:\boldsymbol{{when}}\:\left(\sqrt{\boldsymbol{{x}}}−\mathrm{1}\right)>\mathrm{0}\:\:\boldsymbol{{x}}>\mathrm{1}\right) \\ $$$$\boldsymbol{{but}}\:\boldsymbol{{when}}\:\sqrt{\boldsymbol{{x}}}\:−\mathrm{1}<\mathrm{0}\:\:\:\:\boldsymbol{{x}}<\mathrm{1} \\ $$$$\boldsymbol{{then}}\:\sqrt{\boldsymbol{{x}}}\:+\mid\sqrt{{x}}\:−\mathrm{1}\mid \\ $$$$=\sqrt{{x}}\:−\sqrt{{x}}\:+\mathrm{1} \\ $$$$=\mathrm{1}\:\:{when}\:\:{x}<\mathrm{1} \\ $$$${so}\:\:\:{x}=\mathrm{4}\:{is}\:{the}\:{solution} \\ $$$$ \\ $$$$ \\ $$
