Menu Close

Question-60888

Tinku Tara 0 Comments
Pin




Question Number 60888 by ajfour last updated on 26/May/19
Commented by ajfour last updated on 27/May/19
If length l encloses maximum such area, find the area. (a) if l be circular (b) if shape of l not be given (someone please consider solving this)
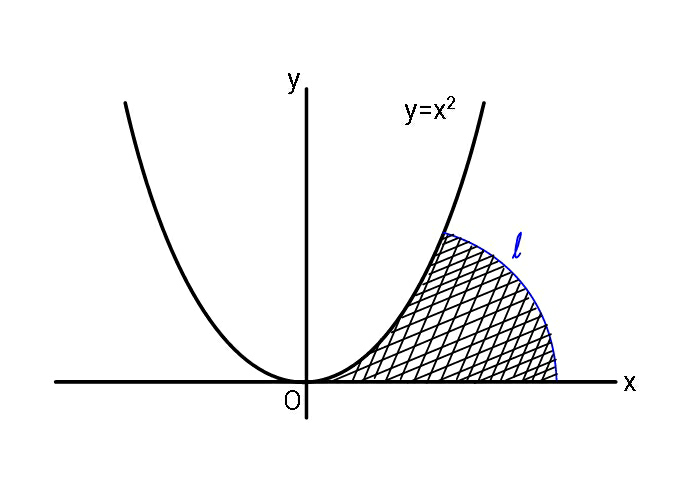
$${If}\:{length}\:\boldsymbol{{l}}\:{encloses}\:{maximum} \\ $$$${such}\:{area},\:{find}\:{the}\:{area}. \\ $$$$\left({a}\right)\:{if}\:{l}\:{be}\:{circular} \\ $$$$\left({b}\right)\:{if}\:{shape}\:{of}\:{l}\:{not}\:{be}\:{given} \\ $$$$\left({someone}\:{please}\:{consider}\right. \\ $$$$\left.\:\:\:{solving}\:{this}\right) \\ $$
Answered by ajfour last updated on 26/May/19
Commented by ajfour last updated on 27/May/19
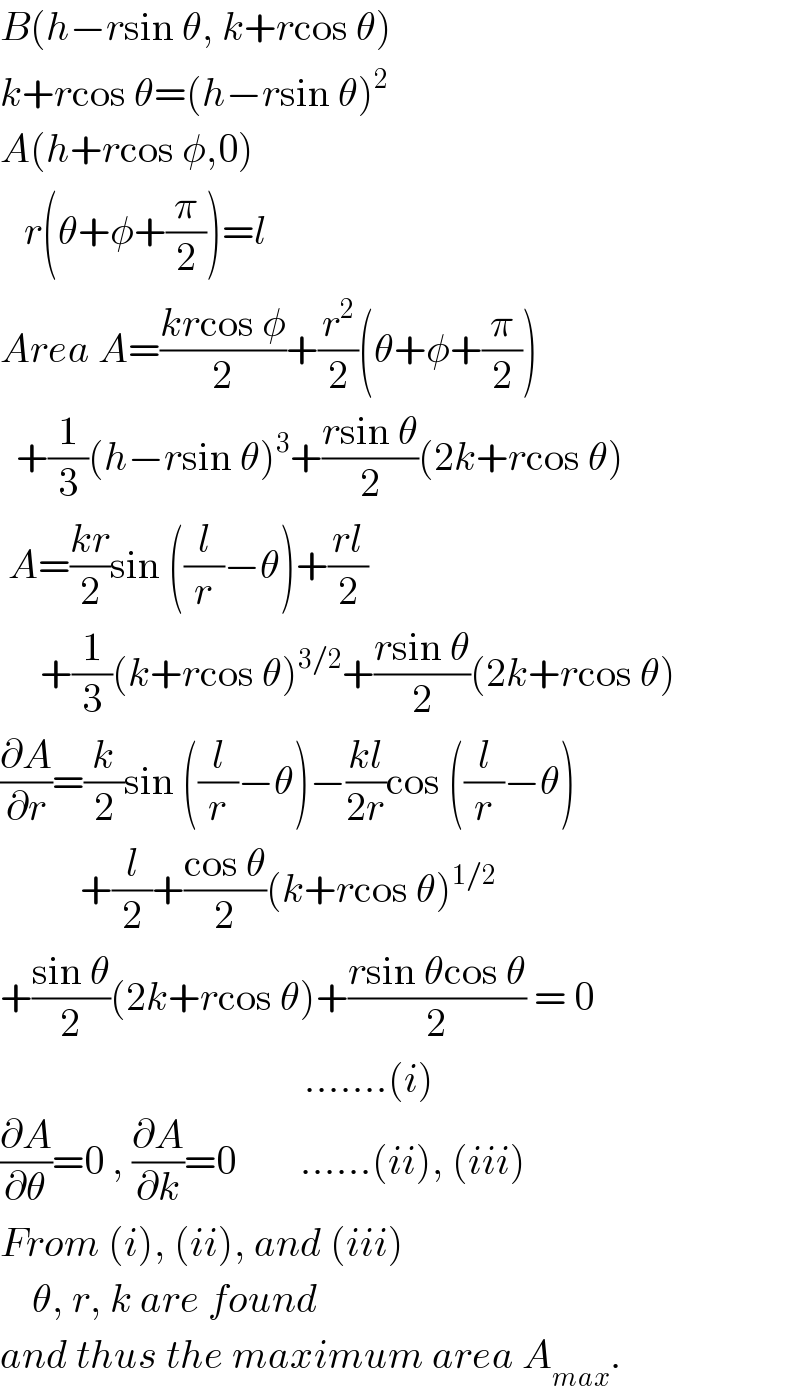
B(h−rsin θ, k+rcos θ) k+rcos θ=(h−rsin θ)^2 A(h+rcos φ,0) r(θ+φ+(π/2))=l Area A=((krcos φ)/2)+(r^2 /2)(θ+φ+(π/2)) +(1/3)(h−rsin θ)^3 +((rsin θ)/2)(2k+rcos θ) A=((kr)/2)sin ((l/r)−θ)+((rl)/2) +(1/3)(k+rcos θ)^(3/2) +((rsin θ)/2)(2k+rcos θ) (∂A/∂r)=(k/2)sin ((l/r)−θ)−((kl)/(2r))cos ((l/r)−θ) +(l/2)+((cos θ)/2)(k+rcos θ)^(1/2) +((sin θ)/2)(2k+rcos θ)+((rsin θcos θ)/2) = 0 .......(i) (∂A/∂θ)=0 , (∂A/∂k)=0 ......(ii), (iii) From (i), (ii), and (iii) θ, r, k are found and thus the maximum area A_(max) .
$${B}\left({h}−{r}\mathrm{sin}\:\theta,\:{k}+{r}\mathrm{cos}\:\theta\right) \\ $$$${k}+{r}\mathrm{cos}\:\theta=\left({h}−{r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${A}\left({h}+{r}\mathrm{cos}\:\phi,\mathrm{0}\right) \\ $$$$\:\:\:{r}\left(\theta+\phi+\frac{\pi}{\mathrm{2}}\right)={l} \\ $$$${Area}\:{A}=\frac{{kr}\mathrm{cos}\:\phi}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta+\phi+\frac{\pi}{\mathrm{2}}\right) \\ $$$$\:\:+\frac{\mathrm{1}}{\mathrm{3}}\left({h}−{r}\mathrm{sin}\:\theta\right)^{\mathrm{3}} +\frac{{r}\mathrm{sin}\:\theta}{\mathrm{2}}\left(\mathrm{2}{k}+{r}\mathrm{cos}\:\theta\right) \\ $$$$\:{A}=\frac{{kr}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{{l}}{{r}}−\theta\right)+\frac{{rl}}{\mathrm{2}} \\ $$$$\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{3}}\left({k}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{3}/\mathrm{2}} +\frac{{r}\mathrm{sin}\:\theta}{\mathrm{2}}\left(\mathrm{2}{k}+{r}\mathrm{cos}\:\theta\right) \\ $$$$\frac{\partial{A}}{\partial{r}}=\frac{{k}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{{l}}{{r}}−\theta\right)−\frac{{kl}}{\mathrm{2}{r}}\mathrm{cos}\:\left(\frac{{l}}{{r}}−\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:+\frac{{l}}{\mathrm{2}}+\frac{\mathrm{cos}\:\theta}{\mathrm{2}}\left({k}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\left(\mathrm{2}{k}+{r}\mathrm{cos}\:\theta\right)+\frac{{r}\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…….\left({i}\right) \\ $$$$\frac{\partial{A}}{\partial\theta}=\mathrm{0}\:,\:\frac{\partial{A}}{\partial{k}}=\mathrm{0}\:\:\:\:\:\:\:\:……\left({ii}\right),\:\left({iii}\right) \\ $$$${From}\:\left({i}\right),\:\left({ii}\right),\:{and}\:\left({iii}\right) \\ $$$$\:\:\:\:\theta,\:{r},\:{k}\:{are}\:{found} \\ $$$${and}\:{thus}\:{the}\:{maximum}\:{area}\:{A}_{{max}} . \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *