Question-60910

Question Number 60910 by Tawa1 last updated on 27/May/19

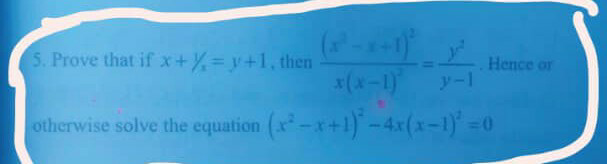
Commented by Rasheed.Sindhi last updated on 27/May/19

Solve the equation (x^2 − x + 1)^2 − 4x(x − 1)^2 = 0 x^4 +x^2 +1−2x^3 −2x+2x^2 −4x(x^2 −2x+1)=0 x^4 +x^2 +1−2x^3 −2x+2x^2 −4x^3 +8x^2 −4x=0 x^4 −6x^3 +11x^2 −6x+1=0 x^2 (x^2 +(1/x^2 )−6x−(6/x)+11)=0 x^2 =0 ∣ x^2 +(1/x^2 )−6(x+(1/x))+11=0 x=0 (Extraneous root) x^2 +2+(1/x^2 )−6(x+(1/x))+11−2=0 (x+(1/x))^2 −6(x+(1/x))+9=0 (x+(1/x)−3)^2 =0 x+(1/x)−3=0 x+(1/x)=3 x^2 −3x+1=0 x=((3±(√5))/2) x=((3±(√5))/2)

$${S}\mathrm{olve}\:\mathrm{the}\:\mathrm{equation}\:\:\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:−\:\mathrm{4x}\left(\mathrm{x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:\:=\:\:\:\mathrm{0} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{4}{x}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{6}{x}−\frac{\mathrm{6}}{{x}}+\mathrm{11}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\mathrm{0}\:\mid\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{6}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{11}=\mathrm{0} \\ $$$${x}=\mathrm{0}\:\:\left(\mathcal{E}{xtraneous}\:{root}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{6}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{11}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{6}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left({x}+\frac{\mathrm{1}}{{x}}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}+\frac{\mathrm{1}}{{x}}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Commented by Tawa1 last updated on 27/May/19

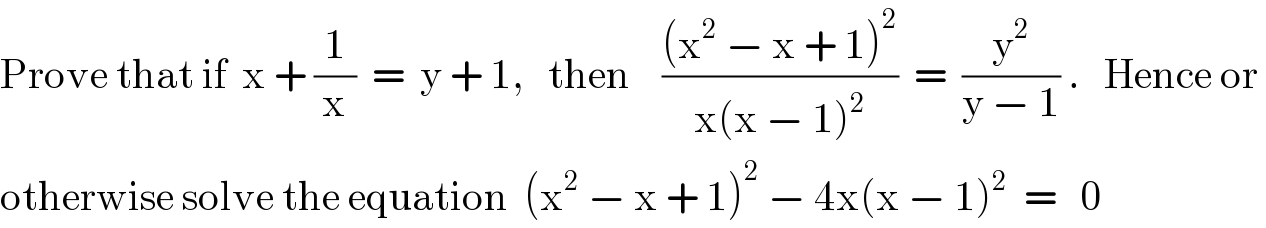
Prove that if x + (1/x) = y + 1, then (((x^2 − x + 1)^2 )/(x(x − 1)^2 )) = (y^2 /(y − 1)) . Hence or otherwise solve the equation (x^2 − x + 1)^2 − 4x(x − 1)^2 = 0

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:\:\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\:\:=\:\:\mathrm{y}\:+\:\mathrm{1},\:\:\:\mathrm{then}\:\:\:\:\frac{\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}\left(\mathrm{x}\:−\:\mathrm{1}\right)^{\mathrm{2}} }\:\:=\:\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{y}\:−\:\mathrm{1}}\:.\:\:\:\mathrm{Hence}\:\mathrm{or}\: \\ $$$$\mathrm{otherwise}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\:\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:−\:\mathrm{4x}\left(\mathrm{x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:\:=\:\:\:\mathrm{0} \\ $$

Commented by Tawa1 last updated on 27/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate}: \\ $$

Commented by MJS last updated on 27/May/19

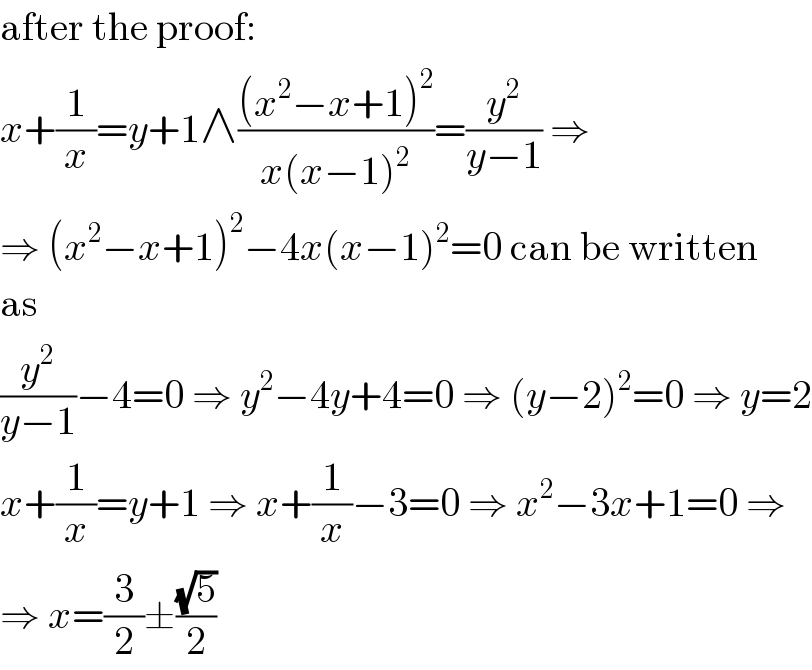
after the proof: x+(1/x)=y+1∧(((x^2 −x+1)^2 )/(x(x−1)^2 ))=(y^2 /(y−1)) ⇒ ⇒ (x^2 −x+1)^2 −4x(x−1)^2 =0 can be written as (y^2 /(y−1))−4=0 ⇒ y^2 −4y+4=0 ⇒ (y−2)^2 =0 ⇒ y=2 x+(1/x)=y+1 ⇒ x+(1/x)−3=0 ⇒ x^2 −3x+1=0 ⇒ ⇒ x=(3/2)±((√5)/2)

$$\mathrm{after}\:\mathrm{the}\:\mathrm{proof}: \\ $$$${x}+\frac{\mathrm{1}}{{x}}={y}+\mathrm{1}\wedge\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written} \\ $$$$\mathrm{as} \\ $$$$\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}}−\mathrm{4}=\mathrm{0}\:\Rightarrow\:{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4}=\mathrm{0}\:\Rightarrow\:\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{y}=\mathrm{2} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={y}+\mathrm{1}\:\Rightarrow\:{x}+\frac{\mathrm{1}}{{x}}−\mathrm{3}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 27/May/19

$${Very}\:{simple}\:{sir}! \\ $$$$\:\:{I}\:{also}\:{had}\:{tried}\:{to}\:{replace}\:{x}\:{by}\:{y}\:{but} \\ $$$${I}\:{couldn}'{t}\:{do}\:{it}\:{perfectly}. \\ $$

Commented by Tawa1 last updated on 27/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by maxmathsup by imad last updated on 28/May/19

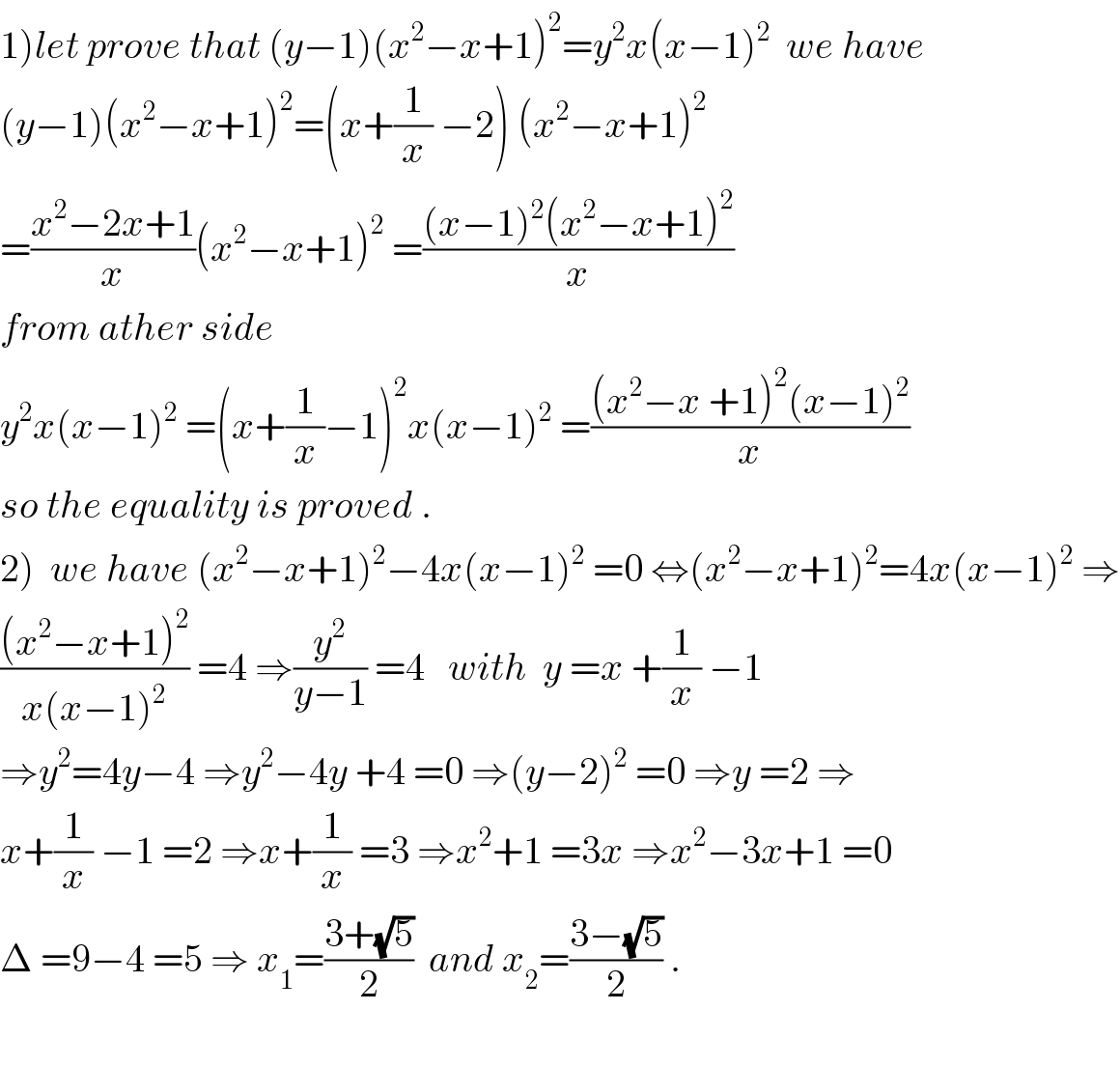
1)let prove that (y−1)(x^2 −x+1)^2 =y^2 x(x−1)^2 we have (y−1)(x^2 −x+1)^2 =(x+(1/x) −2) (x^2 −x+1)^2 =((x^2 −2x+1)/x)(x^2 −x+1)^2 =(((x−1)^2 (x^2 −x+1)^2 )/x) from ather side y^2 x(x−1)^2 =(x+(1/x)−1)^2 x(x−1)^2 =(((x^2 −x +1)^2 (x−1)^2 )/x) so the equality is proved . 2) we have (x^2 −x+1)^2 −4x(x−1)^2 =0 ⇔(x^2 −x+1)^2 =4x(x−1)^2 ⇒ (((x^2 −x+1)^2 )/(x(x−1)^2 )) =4 ⇒(y^2 /(y−1)) =4 with y =x +(1/x) −1 ⇒y^2 =4y−4 ⇒y^2 −4y +4 =0 ⇒(y−2)^2 =0 ⇒y =2 ⇒ x+(1/x) −1 =2 ⇒x+(1/x) =3 ⇒x^2 +1 =3x ⇒x^2 −3x+1 =0 Δ =9−4 =5 ⇒ x_1 =((3+(√5))/2) and x_2 =((3−(√5))/2) .

$$\left.\mathrm{1}\right){let}\:{prove}\:{that}\:\left({y}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} ={y}^{\mathrm{2}} {x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:\:{we}\:{have} \\ $$$$\left({y}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} =\left({x}+\frac{\mathrm{1}}{{x}}\:−\mathrm{2}\right)\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} \:=\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}} \\ $$$${from}\:{ather}\:{side} \\ $$$${y}^{\mathrm{2}} {x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:=\left({x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)^{\mathrm{2}} {x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:=\frac{\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}} \\ $$$${so}\:{the}\:{equality}\:{is}\:{proved}\:. \\ $$$$\left.\mathrm{2}\right)\:\:{we}\:{have}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Leftrightarrow\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{4}\:\Rightarrow\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}}\:=\mathrm{4}\:\:\:{with}\:\:{y}\:={x}\:+\frac{\mathrm{1}}{{x}}\:−\mathrm{1} \\ $$$$\Rightarrow{y}^{\mathrm{2}} =\mathrm{4}{y}−\mathrm{4}\:\Rightarrow{y}^{\mathrm{2}} −\mathrm{4}{y}\:+\mathrm{4}\:=\mathrm{0}\:\Rightarrow\left({y}−\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow{y}\:=\mathrm{2}\:\Rightarrow \\ $$$${x}+\frac{\mathrm{1}}{{x}}\:−\mathrm{1}\:=\mathrm{2}\:\Rightarrow{x}+\frac{\mathrm{1}}{{x}}\:=\mathrm{3}\:\Rightarrow{x}^{\mathrm{2}} +\mathrm{1}\:=\mathrm{3}{x}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{9}−\mathrm{4}\:=\mathrm{5}\:\Rightarrow\:{x}_{\mathrm{1}} =\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:. \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 27/May/19

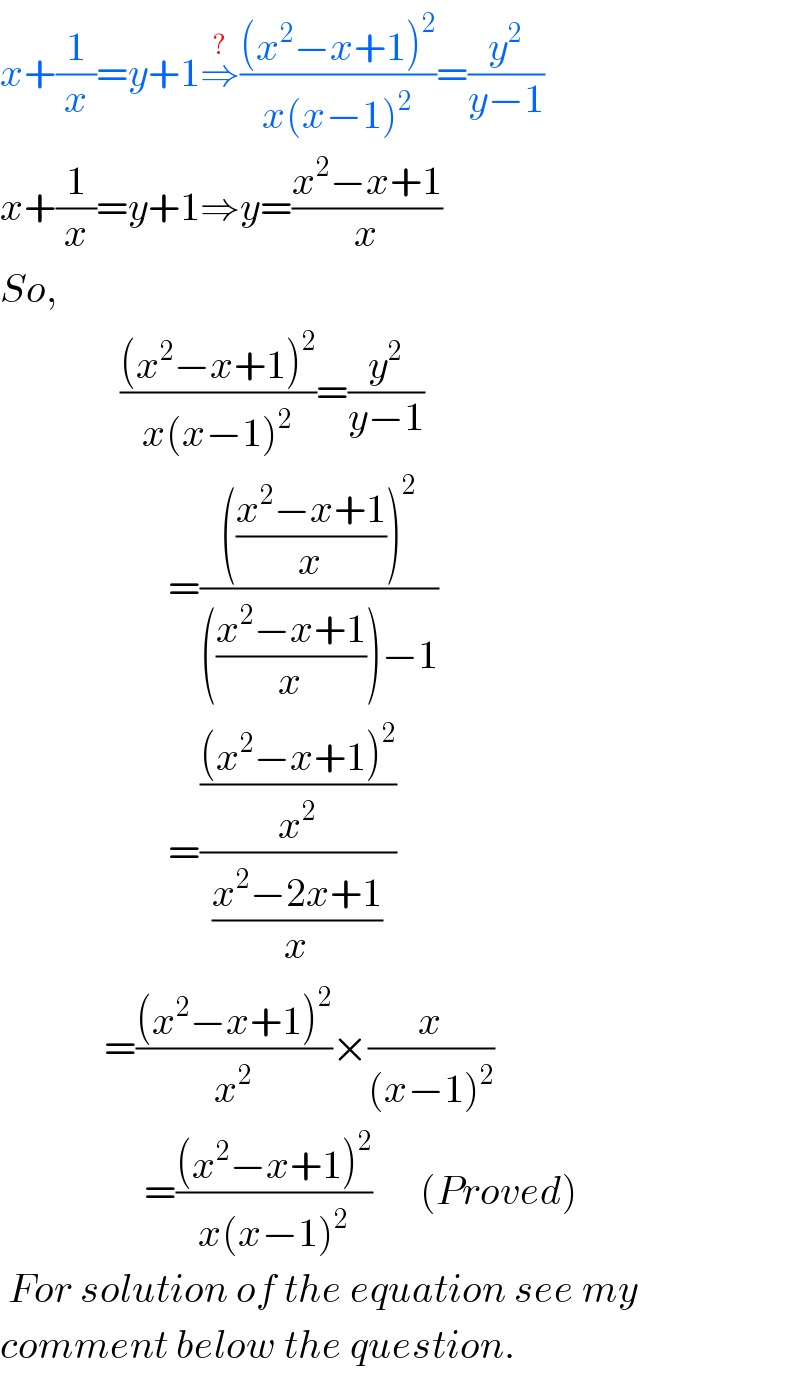
x+(1/x)=y+1⇒^(?) (((x^2 −x+1)^2 )/(x(x−1)^2 ))=(y^2 /(y−1)) x+(1/x)=y+1⇒y=((x^2 −x+1)/x) So, (((x^2 −x+1)^2 )/(x(x−1)^2 ))=(y^2 /(y−1)) =(((((x^2 −x+1)/x))^2 )/((((x^2 −x+1)/x))−1)) =((((x^2 −x+1)^2 )/x^2 )/((x^2 −2x+1)/x)) =(((x^2 −x+1)^2 )/x^2 )×(x/((x−1)^2 )) =(((x^2 −x+1)^2 )/(x(x−1)^2 )) (Proved) For solution of the equation see my comment below the question.

$${x}+\frac{\mathrm{1}}{{x}}={y}+\mathrm{1}\overset{?} {\Rightarrow}\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={y}+\mathrm{1}\Rightarrow{y}=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}} \\ $$$${So}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{\left(\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}}\right)−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }}{\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }×\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\:\left({Proved}\right)\:\:\: \\ $$$$\:{For}\:{solution}\:{of}\:{the}\:{equation}\:{see}\:{my} \\ $$$${comment}\:{below}\:{the}\:{question}. \\ $$

Commented by Tawa1 last updated on 27/May/19

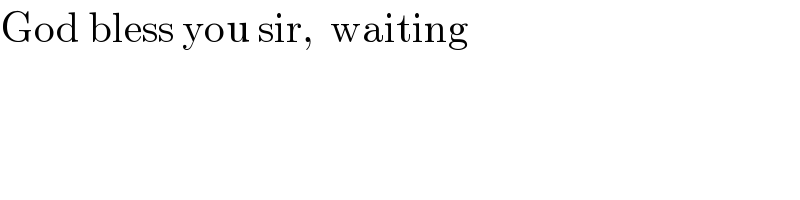
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{waiting} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply