Question Number 60948 by Kunal12588 last updated on 27/May/19
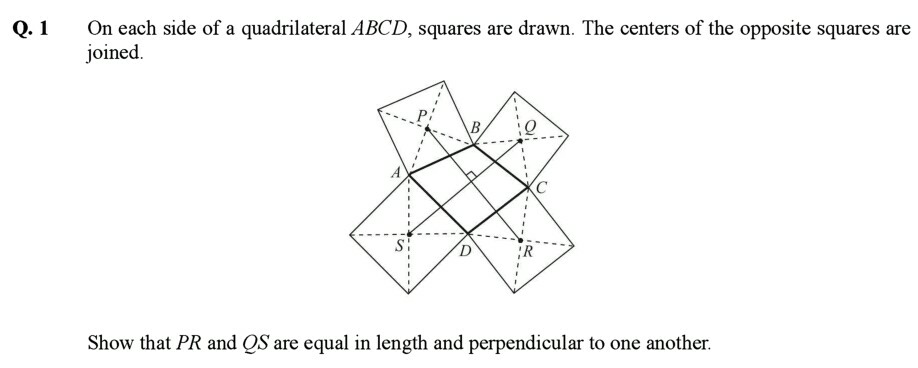
Commented by Prithwish sen last updated on 27/May/19

$$\mathrm{Let}\:\mathrm{A}\:\mathrm{be}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{of}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{plane}\: \\ $$$$\mathrm{and}, \\ $$$$\mathrm{AB}=\mathrm{2a} \\ $$$$\mathrm{BC}=\mathrm{2b} \\ $$$$\mathrm{CD}=\mathrm{2c} \\ $$$$\mathrm{AD}=\mathrm{2d}\:,\:\mathrm{where}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\in\:\mathrm{C}\:\left(\mathrm{complex}\:\mathrm{number}\:\right) \\ $$$$\because\:\mathrm{ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadrilateral}\:\mathrm{then}, \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\:=\mathrm{0} \\ $$$$\mathrm{Now}, \\ $$$$\mathrm{P}\:=\:\mathrm{a}+\mathrm{ia} \\ $$$$\mathrm{Q}\:=\mathrm{2a}+\left(\mathrm{1}+\mathrm{i}\right)\mathrm{b} \\ $$$$\mathrm{R}\:=\:\mathrm{2a}+\mathrm{2b}+\left(\mathrm{1}+\mathrm{i}\right)\mathrm{c} \\ $$$$\mathrm{S}=\:\mathrm{2a}+\mathrm{2b}+\mathrm{2c}+\left(\mathrm{1}+\mathrm{i}\right)\mathrm{d} \\ $$$$\mathrm{Now}\:\mathrm{let}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number}, \\ $$$$\mathrm{z}_{\mathrm{1}} =\mathrm{S}−\mathrm{Q}=\left(\mathrm{b}+\mathrm{2c}+\mathrm{d}\right)+\mathrm{i}\left(\mathrm{d}−\mathrm{b}\right) \\ $$$$\mathrm{z}_{\mathrm{2}\:} =\mathrm{R}−\mathrm{P}=\left(\mathrm{a}+\mathrm{2b}+\mathrm{c}\right)+\mathrm{i}\left(\mathrm{c}−\mathrm{a}\right) \\ $$$$\mathrm{Now}\:\mathrm{z}_{\mathrm{1}} +\mathrm{iz}_{\mathrm{2}} =\left(\mathrm{b}+\mathrm{2c}+\mathrm{d}−\mathrm{c}+\mathrm{a}\right)+\mathrm{i}\left(\mathrm{d}−\mathrm{b}+\mathrm{a}+\mathrm{2b}+\mathrm{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\right)\:+\mathrm{i}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\right)\:=\mathrm{0} \\ $$$$\mathrm{i}.\mathrm{e}\:\:\mathrm{z}_{\mathrm{1}} \bot\mathrm{z}_{\mathrm{2}} \\ $$$$\mathrm{or},\:\mathrm{PR}\bot\mathrm{SQ}\:\:\mathrm{Proved}. \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$
