Question Number 60981 by necx1 last updated on 28/May/19
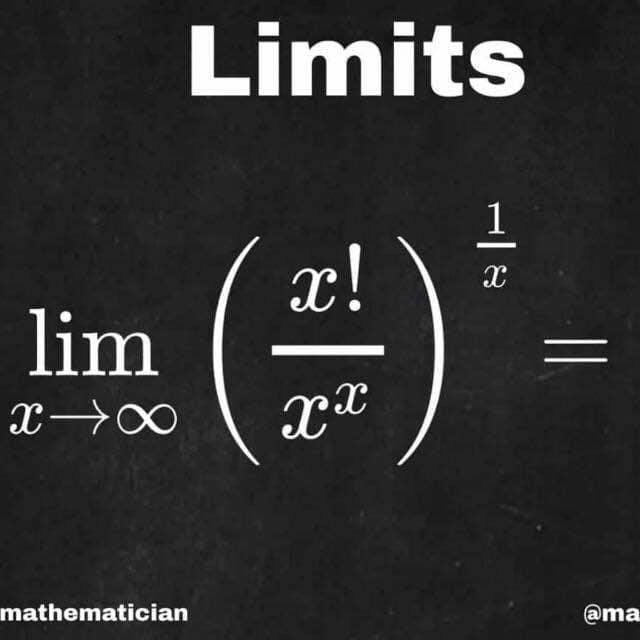
Commented by Prithwish sen last updated on 28/May/19
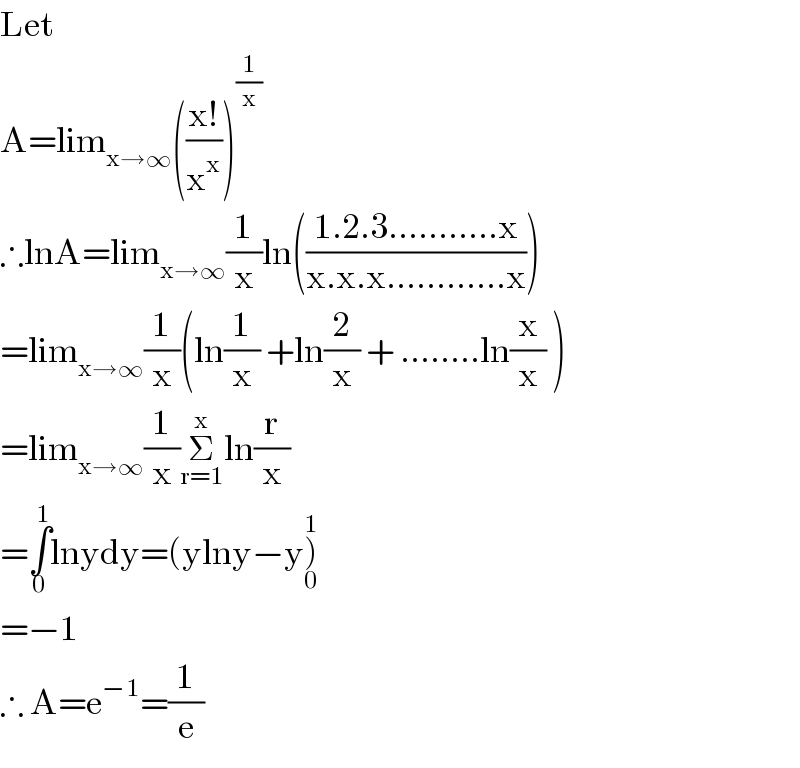
$$\mathrm{Let}\: \\ $$$$\mathrm{A}=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \left(\frac{\mathrm{x}!}{\mathrm{x}^{\mathrm{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{x}}} \\ $$$$\therefore\mathrm{lnA}=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}………..\mathrm{x}}{\mathrm{x}.\mathrm{x}.\mathrm{x}…………\mathrm{x}}\right) \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{x}}\left(\mathrm{ln}\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{ln}\frac{\mathrm{2}}{\mathrm{x}}\:+\:……..\mathrm{ln}\frac{\mathrm{x}}{\mathrm{x}}\:\right) \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{x}} {\sum}}\mathrm{ln}\frac{\mathrm{r}}{\mathrm{x}} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{lnydy}=\left(\mathrm{ylny}−\mathrm{y}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\right)}} \\ $$$$=−\mathrm{1} \\ $$$$\therefore\:\mathrm{A}=\mathrm{e}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{e}} \\ $$
Commented by tanmay last updated on 28/May/19
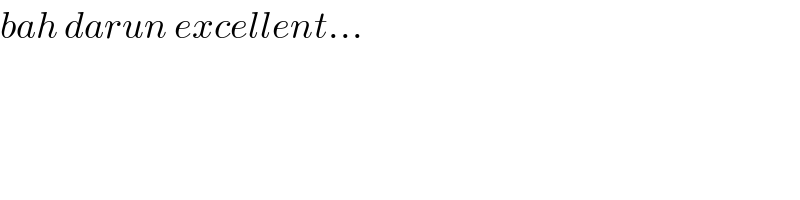
$${bah}\:{darun}\:{excellent}… \\ $$
Commented by Prithwish sen last updated on 28/May/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by ajfour last updated on 28/May/19
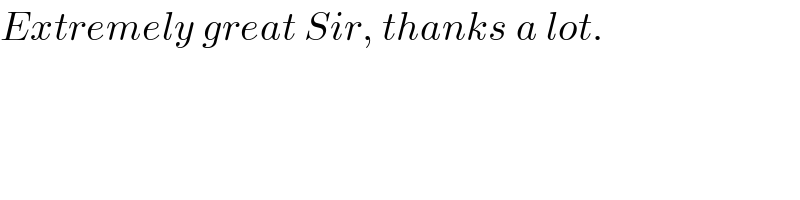
$${Extremely}\:{great}\:{Sir},\:{thanks}\:{a}\:{lot}. \\ $$
Commented by Prithwish sen last updated on 28/May/19

$$\mathrm{welcome}.\: \\ $$
Commented by Mr X pcx last updated on 28/May/19
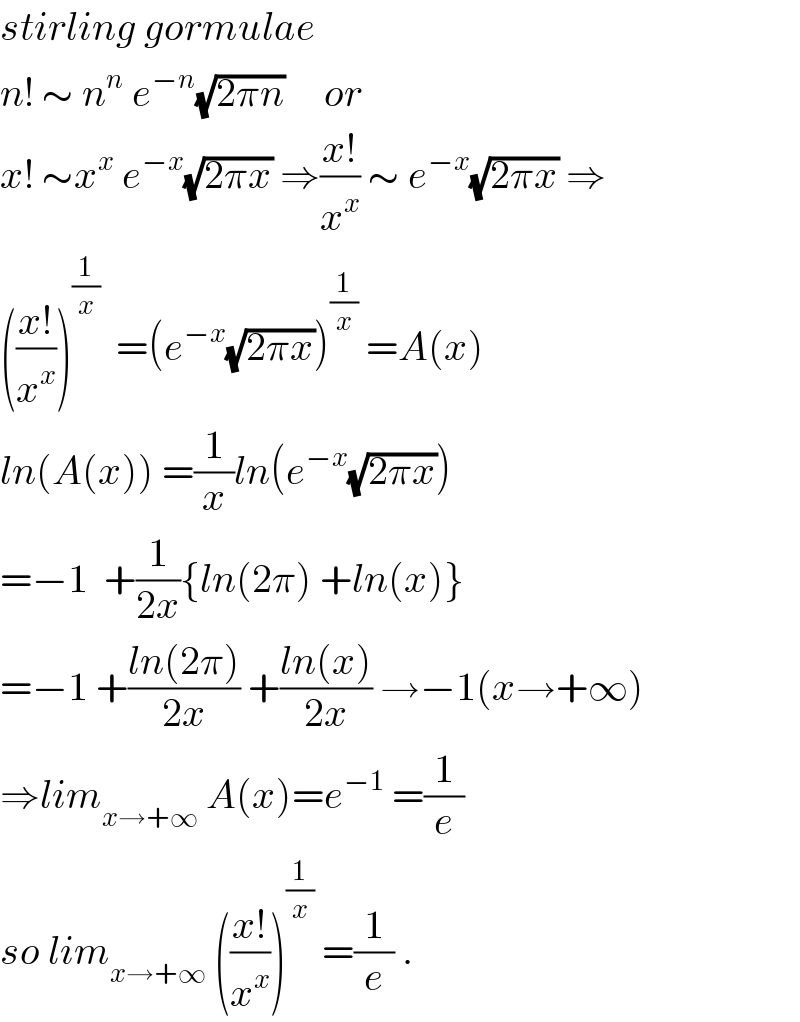
$${stirling}\:{gormulae} \\ $$$${n}!\:\sim\:{n}^{{n}} \:{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:\:\:\:\:{or}\: \\ $$$${x}!\:\sim{x}^{{x}} \:{e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\:\Rightarrow\frac{{x}!}{{x}^{{x}} }\:\sim\:{e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\:\Rightarrow \\ $$$$\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \:\:=\left({e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\right)^{\frac{\mathrm{1}}{{x}}} \:={A}\left({x}\right) \\ $$$${ln}\left({A}\left({x}\right)\right)\:=\frac{\mathrm{1}}{{x}}{ln}\left({e}^{−{x}} \sqrt{\mathrm{2}\pi{x}}\right) \\ $$$$=−\mathrm{1}\:\:+\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{{ln}\left(\mathrm{2}\pi\right)\:+{ln}\left({x}\right)\right\} \\ $$$$=−\mathrm{1}\:+\frac{{ln}\left(\mathrm{2}\pi\right)}{\mathrm{2}{x}}\:+\frac{{ln}\left({x}\right)}{\mathrm{2}{x}}\:\rightarrow−\mathrm{1}\left({x}\rightarrow+\infty\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow+\infty} \:{A}\left({x}\right)={e}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{{e}} \\ $$$${so}\:{lim}_{{x}\rightarrow+\infty} \:\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \:=\frac{\mathrm{1}}{{e}}\:. \\ $$
Answered by MJS last updated on 28/May/19

$$\mathrm{tried}\:\mathrm{with}\:\mathrm{Stirling}'\mathrm{s}\:\mathrm{formula} \\ $$$${x}!\approx\left(\frac{{x}}{\mathrm{e}}\right)^{{x}} \sqrt{\mathrm{2}\pi{x}} \\ $$$$\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} =\frac{{x}!^{\frac{\mathrm{1}}{{x}}} }{{x}}\approx\frac{\mathrm{1}}{{x}}\left(\left(\frac{{x}}{\mathrm{e}}\right)^{{x}} \sqrt{\mathrm{2}\pi{x}}\right)^{\frac{\mathrm{1}}{{x}}} =\frac{\mathrm{1}}{{x}}×\frac{{x}}{\mathrm{e}}\left(\mathrm{2}\pi{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{e}}×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} ×\pi^{\frac{\mathrm{1}}{\mathrm{2}{x}}} ×{x}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{e}}×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} ×\pi^{\frac{\mathrm{1}}{\mathrm{2}{x}}} ×{x}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\frac{\mathrm{1}}{\mathrm{e}} \\ $$$$\mathrm{this}\:\mathrm{seems}\:\mathrm{right},\:\mathrm{computing}\:\mathrm{shows} \\ $$$$\left(\frac{\mathrm{100}!}{\mathrm{100}^{\mathrm{100}} }\right)^{\frac{\mathrm{1}}{\mathrm{100}}} \approx.\mathrm{379927} \\ $$$$\left(\frac{\mathrm{200}!}{\mathrm{200}^{\mathrm{200}} }\right)^{\frac{\mathrm{1}}{\mathrm{200}}} \approx.\mathrm{374502} \\ $$$$\left(\frac{\mathrm{300}!}{\mathrm{300}^{\mathrm{300}} }\right)^{\frac{\mathrm{1}}{\mathrm{300}}} \approx.\mathrm{372533} \\ $$$$\left(\frac{\mathrm{400}!}{\mathrm{400}^{\mathrm{400}} }\right)^{\frac{\mathrm{1}}{\mathrm{400}}} \approx.\mathrm{371498} \\ $$$$\frac{\mathrm{1}}{\mathrm{e}}\approx.\mathrm{367879} \\ $$
Commented by tanmay last updated on 28/May/19
$${bah}\:{darun}\:{excellent}…{one}\:{problem}\:{but}\:{solution} \\ $$$${three}\:{method}… \\ $$
Answered by tanmay last updated on 28/May/19
![lim_(x→∞) (a_(x+1) /a_x ) =lim_(x→∞) (({(((x+1)!)/((x+1)^(x+1) ))})/((((x!)/x^x )))) =lim_(x→∞) (((x+1)!)/(x!))×(1/(((x+1)^(x+1) )/x^x )) =lim_(x→∞) (x+1)×(1/((x+1)(((x+1)/x))^x )) =lim_(x→∞) (1/((1+(1/x))^x )) now t=(1/x) y=lim_(t→0) (1/((1+t)^(1/t) )) lny=lim_(t→0) [((−ln(1+t))/t)] lny=−1 y=e^(−1) so lim_(x→∞) (((x!)/x^x ))^(1/x) =e^(−1) →it is the answer using cauchy second theorem on limit lim_(n→∞) (a_n )^(1/n) =l if lim_(n→∞) (a_(n+1) /a_n )=l](https://www.tinkutara.com/question/Q60995.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{a}_{{x}+\mathrm{1}} }{{a}_{{x}} } \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\left\{\frac{\left({x}+\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)^{{x}+\mathrm{1}} }\right\}}{\left(\frac{{x}!}{{x}^{{x}} }\right)} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({x}+\mathrm{1}\right)!}{{x}!}×\frac{\mathrm{1}}{\frac{\left({x}+\mathrm{1}\right)^{{x}+\mathrm{1}} }{{x}^{{x}} }} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left({x}+\mathrm{1}\right)×\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}} } \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} } \\ $$$${now}\:{t}=\frac{\mathrm{1}}{{x}} \\ $$$${y}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{{t}}} } \\ $$$${lny}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{−{ln}\left(\mathrm{1}+{t}\right)}{{t}}\right] \\ $$$${lny}=−\mathrm{1} \\ $$$${y}={e}^{−\mathrm{1}} \\ $$$${so}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}!}{{x}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} ={e}^{−\mathrm{1}} \rightarrow{it}\:{is}\:{the}\:{answer} \\ $$$${using}\:{cauchy}\:{second}\:{theorem}\:{on}\:{limit} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({a}_{{n}} \right)^{\frac{\mathrm{1}}{{n}}} ={l} \\ $$$${if}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }={l} \\ $$
Commented by necx1 last updated on 28/May/19
$${God}\:{bless}\:{you}\:{sir} \\ $$
