Question Number 60987 by ajfour last updated on 28/May/19
Commented by ajfour last updated on 28/May/19
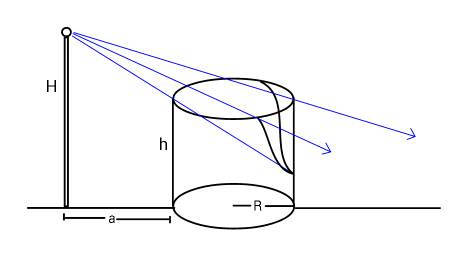
![Find the illuminated area of the inner curved surface of shown, hollow open cylinder. [where a>2R((H/h)−1)]](https://www.tinkutara.com/question/Q60988.png)
$${Find}\:{the}\:{illuminated}\:{area}\:{of} \\ $$$${the}\:{inner}\:{curved}\:{surface}\:{of}\: \\ $$$${shown},\:{hollow}\:{open}\:{cylinder}. \\ $$$$\:\:\:\:\:\:\left[{where}\:\:{a}>\mathrm{2}{R}\left(\frac{{H}}{{h}}−\mathrm{1}\right)\right]\:\:\:\:\: \\ $$
Answered by mr W last updated on 28/May/19
Commented by mr W last updated on 30/May/19
![tan α=((R sin θ)/(a+R(1+cos θ)))=((sin θ)/((a/R)+1+cos θ)) θ_0 =(π/2)+α_0 =(π/2)+sin^(−1) (R/(a+R)) R^2 =SA^2 +(a+R)^2 −2 SA (a+R)cos α ⇒SA^2 −2(a+R)cos α SA+a(a+2R)=0 SA=(a+R) cos α±(√((a+R)^2 cos^2 α−a(a+2R))) SA=(a+R){cos α−(√(cos^2 α−((a(a+2R))/((a+R)^2 ))))} SB=(a+R){cos α+(√(cos^2 α−((a(a+2R))/((a+R)^2 ))))} AB=SB−SA=2(a+R)(√(cos^2 α−((a(a+2R))/((a+R)^2 )))) ((h−z)/(H−h))=((AB)/(SA)) ⇒h−z=(H−h)((AB)/(SA))=(H−h)((2(a+R)(√(cos^2 α−((a(a+2R))/((a+R)^2 )))))/((a+R){cos α−(√(cos^2 α−((a(a+2R))/((a+R)^2 ))))})) ⇒h−z=((2(H−h))/({(1/( (√(1−((a(a+2R))/((a+R)^2 ))×(1/(cos^2 α))))))−1})) ⇒Δz=h−z=((2(H−h))/((1/( (√(1−((a(a+2R))/((a+R)^2 ))[1+(((sin θ)/((a/R)+1+cos θ)))^2 ]))))−1)) Illuminated area=A let λ=(a/R) A=2∫_0 ^θ_0 ΔzRdθ ⇒A=4R(H−h)∫_0 ^θ_0 (dθ/((1/( (√(1−((a(a+2R))/((a+R)^2 ))[1+(((sin θ)/((a/R)+1+cos θ)))^2 ]))))−1)) ⇒A=4R(H−h)∫_0 ^((π/2)+sin^(−1) (1/(1+λ))) (dθ/((1/( (√(1−[1−(1/((1+λ)^2 ))][1+(((sin θ)/(1+λ+cos θ)))^2 ]))))−1)) with μ=1+λ=((a+R)/R) (A/(4R(H−h)))=∫_0 ^((π/2)+sin^(−1) (1/μ)) (dθ/((1/( (√(1−[1−(1/μ^2 )][1+(((sin θ)/(μ+cos θ)))^2 ]))))−1)) =(1/(μ^2 −1))∫_0 ^((π/2)+sin^(−1) (1/μ)) (1+μ cos θ) dθ =(1/(μ^2 −1))[μ sin θ+θ]_0 ^((π/2)+sin^(−1) (1/μ)) =(1/(μ^2 −1))[μ sin ((π/2)+sin^(−1) (1/μ))+(π/2)+sin^(−1) (1/μ)] =(1/(μ^2 −1))[(√(μ^2 −1))+(π/2)+sin^(−1) (1/μ)] ⇒A=((4R(H−h))/(μ^2 −1))((√(μ^2 −1))+(π/2)+sin^(−1) (1/μ)) with μ=((a+R)/R)](https://www.tinkutara.com/question/Q61075.png)
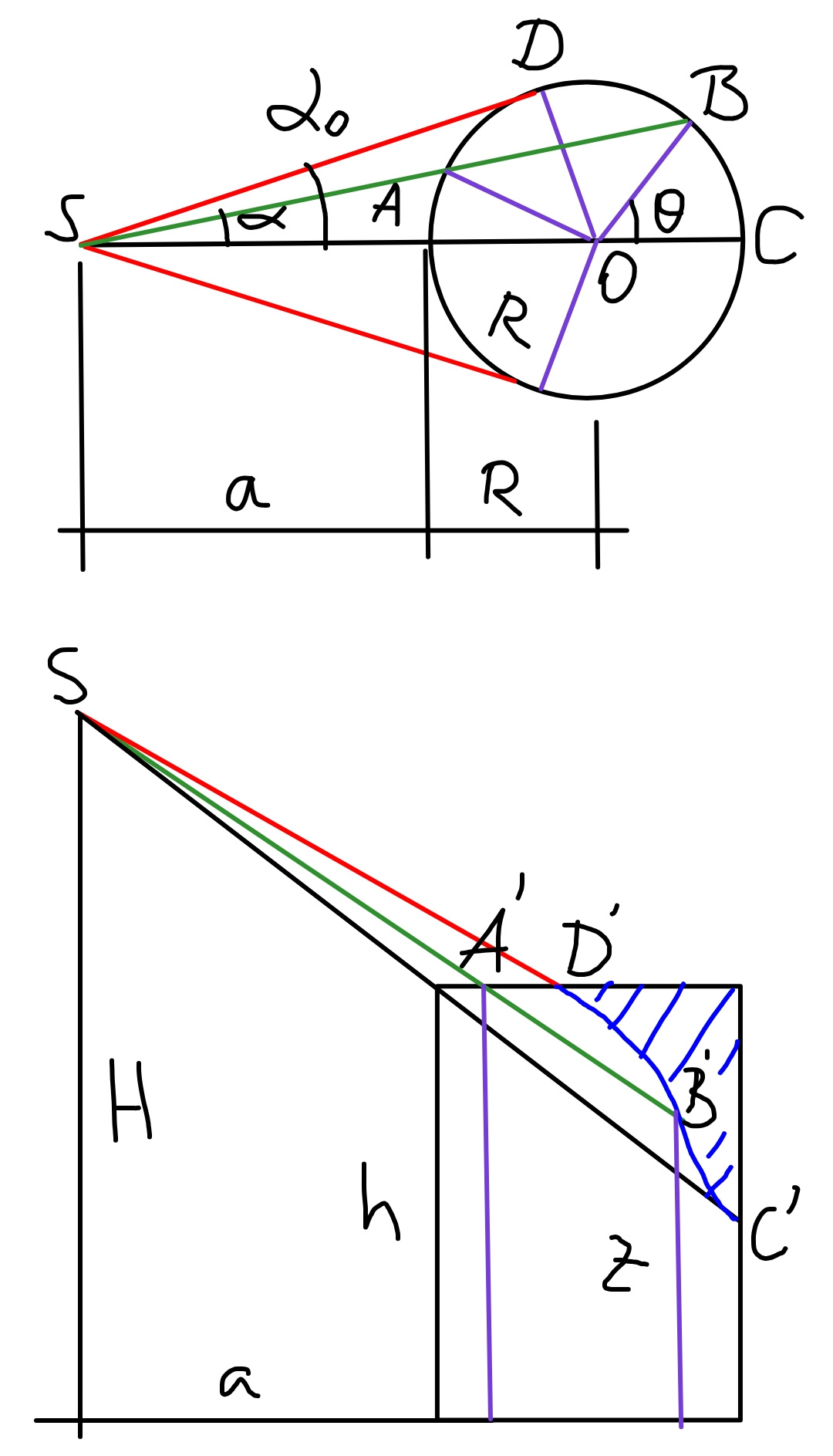
$$\mathrm{tan}\:\alpha=\frac{{R}\:\mathrm{sin}\:\theta}{{a}+{R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}=\frac{\mathrm{sin}\:\theta}{\frac{{a}}{{R}}+\mathrm{1}+\mathrm{cos}\:\theta} \\ $$$$\theta_{\mathrm{0}} =\frac{\pi}{\mathrm{2}}+\alpha_{\mathrm{0}} =\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{{R}}{{a}+{R}} \\ $$$${R}^{\mathrm{2}} ={SA}^{\mathrm{2}} +\left({a}+{R}\right)^{\mathrm{2}} −\mathrm{2}\:{SA}\:\left({a}+{R}\right)\mathrm{cos}\:\alpha \\ $$$$\Rightarrow{SA}^{\mathrm{2}} −\mathrm{2}\left({a}+{R}\right)\mathrm{cos}\:\alpha\:{SA}+{a}\left({a}+\mathrm{2}{R}\right)=\mathrm{0} \\ $$$${SA}=\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\pm\sqrt{\left({a}+{R}\right)^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha−{a}\left({a}+\mathrm{2}{R}\right)} \\ $$$${SA}=\left({a}+{R}\right)\left\{\mathrm{cos}\:\alpha−\sqrt{\mathrm{cos}^{\mathrm{2}} \:\alpha−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }}\right\} \\ $$$${SB}=\left({a}+{R}\right)\left\{\mathrm{cos}\:\alpha+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\alpha−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }}\right\} \\ $$$${AB}={SB}−{SA}=\mathrm{2}\left({a}+{R}\right)\sqrt{\mathrm{cos}^{\mathrm{2}} \:\alpha−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }} \\ $$$$\frac{{h}−{z}}{{H}−{h}}=\frac{{AB}}{{SA}} \\ $$$$\Rightarrow{h}−{z}=\left({H}−{h}\right)\frac{{AB}}{{SA}}=\left({H}−{h}\right)\frac{\mathrm{2}\left({a}+{R}\right)\sqrt{\mathrm{cos}^{\mathrm{2}} \:\alpha−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }}}{\left({a}+{R}\right)\left\{\mathrm{cos}\:\alpha−\sqrt{\mathrm{cos}^{\mathrm{2}} \:\alpha−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }}\right\}} \\ $$$$\Rightarrow{h}−{z}=\frac{\mathrm{2}\left({H}−{h}\right)}{\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\alpha}}}−\mathrm{1}\right\}} \\ $$$$\Rightarrow\Delta{z}={h}−{z}=\frac{\mathrm{2}\left({H}−{h}\right)}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\frac{{a}}{{R}}+\mathrm{1}+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$${Illuminated}\:{area}={A} \\ $$$${let}\:\lambda=\frac{{a}}{{R}} \\ $$$${A}=\mathrm{2}\int_{\mathrm{0}} ^{\theta_{\mathrm{0}} } \Delta{zRd}\theta \\ $$$$\Rightarrow{A}=\mathrm{4}{R}\left({H}−{h}\right)\int_{\mathrm{0}} ^{\theta_{\mathrm{0}} } \frac{{d}\theta}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{{a}\left({a}+\mathrm{2}{R}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\frac{{a}}{{R}}+\mathrm{1}+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$$\Rightarrow{A}=\mathrm{4}{R}\left({H}−{h}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\lambda}} \frac{{d}\theta}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left[\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }\right]\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\lambda+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$${with}\:\mu=\mathrm{1}+\lambda=\frac{{a}+{R}}{{R}} \\ $$$$\frac{{A}}{\mathrm{4}{R}\left({H}−{h}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}} \frac{{d}\theta}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left[\mathrm{1}−\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\right]\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\mu+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mu^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}} \left(\mathrm{1}+\mu\:\mathrm{cos}\:\theta\right)\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mu^{\mathrm{2}} −\mathrm{1}}\left[\mu\:\mathrm{sin}\:\theta+\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}} \\ $$$$=\frac{\mathrm{1}}{\mu^{\mathrm{2}} −\mathrm{1}}\left[\mu\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}\right)+\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}\right] \\ $$$$=\frac{\mathrm{1}}{\mu^{\mathrm{2}} −\mathrm{1}}\left[\sqrt{\mu^{\mathrm{2}} −\mathrm{1}}+\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}\right] \\ $$$$ \\ $$$$\Rightarrow{A}=\frac{\mathrm{4}{R}\left({H}−{h}\right)}{\mu^{\mathrm{2}} −\mathrm{1}}\left(\sqrt{\mu^{\mathrm{2}} −\mathrm{1}}+\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mu}\right) \\ $$$${with}\:\mu=\frac{{a}+{R}}{{R}} \\ $$
Commented by ajfour last updated on 30/May/19
$${Great},\:{work}\:{Sir}!\:{thanks}\:{so}\:{much}. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$
Commented by mr W last updated on 30/May/19
![thanks for checking sir! the integral seems to be complicated, but it′s really easy after the expression is simplified, see below. (1/((1/( (√(1−[1−(1/μ^2 )][1+(((sin θ)/(μ+cos θ)))^2 ]))))−1)) =(1/((μ/( (√(μ^2 −(μ^2 −1)[1+(((sin θ)/(μ+cos θ)))^2 ]))))−1)) =(1/((μ/( (√(1−(μ^2 −1)(((sin θ)/(μ+cos θ)))^2 ))))−1)) =(1/((((μ+cos θ)μ)/( (√((μ+cos θ)^2 −(μ^2 −1)sin^2 θ))))−1)) =(1/((((μ+cos θ)μ)/( (√(μ^2 +2μcos θ+cos^2 θ−μ^2 sin^2 θ+sin^2 θ))))−1)) =(1/((((μ+cos θ)μ)/( (√(μ^2 cos^2 θ+2μcos θ+1))))−1)) =(1/((((μ+cos θ)μ)/(μcos θ+1))−1)) =((μcos θ+1)/((μ+cos θ)μ−(μcos θ+1))) =((μ cos θ+1)/(μ^2 −1))](https://www.tinkutara.com/question/Q61176.png)
$${thanks}\:{for}\:{checking}\:{sir}! \\ $$$${the}\:{integral}\:{seems}\:{to}\:{be}\:{complicated}, \\ $$$${but}\:{it}'{s}\:{really}\:{easy}\:{after}\:{the}\:{expression} \\ $$$${is}\:{simplified},\:{see}\:{below}. \\ $$$$\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left[\mathrm{1}−\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\right]\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\mu+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} −\left(\mu^{\mathrm{2}} −\mathrm{1}\right)\left[\mathrm{1}+\left(\frac{\mathrm{sin}\:\theta}{\mu+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \right]}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mu}{\:\sqrt{\mathrm{1}−\left(\mu^{\mathrm{2}} −\mathrm{1}\right)\left(\frac{\mathrm{sin}\:\theta}{\mu+\mathrm{cos}\:\theta}\right)^{\mathrm{2}} }}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\left(\mu+\mathrm{cos}\:\theta\right)\mu}{\:\sqrt{\left(\mu+\mathrm{cos}\:\theta\right)^{\mathrm{2}} −\left(\mu^{\mathrm{2}} −\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \:\theta}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\left(\mu+\mathrm{cos}\:\theta\right)\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{2}\mu\mathrm{cos}\:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\left(\mu+\mathrm{cos}\:\theta\right)\mu}{\:\sqrt{\mu^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{2}\mu\mathrm{cos}\:\theta+\mathrm{1}}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\left(\mu+\mathrm{cos}\:\theta\right)\mu}{\mu\mathrm{cos}\:\theta+\mathrm{1}}−\mathrm{1}} \\ $$$$=\frac{\mu\mathrm{cos}\:\theta+\mathrm{1}}{\left(\mu+\mathrm{cos}\:\theta\right)\mu−\left(\mu\mathrm{cos}\:\theta+\mathrm{1}\right)} \\ $$$$=\frac{\mu\:\mathrm{cos}\:\theta+\mathrm{1}}{\mu^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by ajfour last updated on 30/May/19
$${True}\:{Sir},\:{thanks}\:{again}. \\ $$
Commented by mr W last updated on 30/May/19
$${it}'{s}\:{again}\:{a}\:{nice}\:{question}\:{sir}! \\ $$
