Question Number 61003 by Tawa1 last updated on 28/May/19

Answered by tanmay last updated on 28/May/19
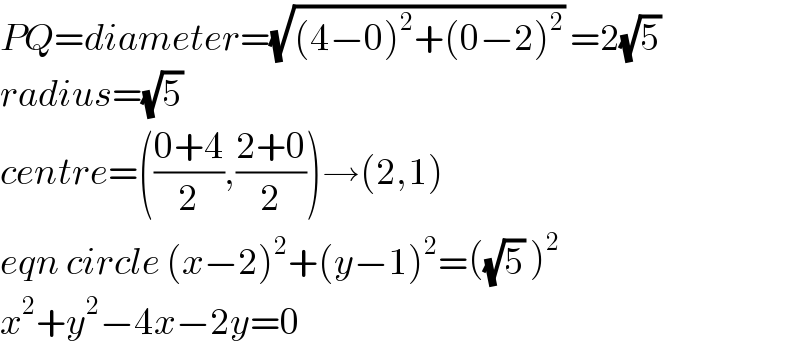
$${PQ}={diameter}=\sqrt{\left(\mathrm{4}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{0}−\mathrm{2}\right)^{\mathrm{2}} }\:=\mathrm{2}\sqrt{\mathrm{5}}\: \\ $$$${radius}=\sqrt{\mathrm{5}}\: \\ $$$${centre}=\left(\frac{\mathrm{0}+\mathrm{4}}{\mathrm{2}},\frac{\mathrm{2}+\mathrm{0}}{\mathrm{2}}\right)\rightarrow\left(\mathrm{2},\mathrm{1}\right) \\ $$$${eqn}\:{circle}\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{2}{y}=\mathrm{0} \\ $$
Commented by Tawa1 last updated on 28/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 28/May/19

$$\left.{ii}\right){eqn}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{2}{y}=\mathrm{0} \\ $$$${eqn}\:{of}\:{tangent}\:{at}\:{Q}\left(\mathrm{4},\mathrm{0}\right) \\ $$$${x}\left(\mathrm{4}\right)+{y}\left(\mathrm{0}\right)−\mathrm{2}\left({x}+\mathrm{4}\right)−\left({y}+\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{4}{x}−\mathrm{2}{x}−\mathrm{8}−{y}=\mathrm{0} \\ $$$$\mathrm{2}{x}−{y}=\mathrm{8} \\ $$$$ \\ $$$$ \\ $$$${formula}\:{to}\:{find}\:{tangent}\:{at}\:{point}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right) \\ $$$${when}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{lies}\:{on}\:{circle} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0} \\ $$$${tricks}… \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0} \\ $$$${x}×{x}+{y}×{y}+{g}\left({x}+{x}\right)+{f}\left({y}+{y}\right)+{c}=\mathrm{0} \\ $$$${now} \\ $$$${xx}_{\mathrm{1}} +{yy}_{\mathrm{1}} +{g}\left({x}+{x}_{\mathrm{1}} \right)+{f}\left({y}+{y}_{\mathrm{1}} \right)+{c}=\mathrm{0}\:{is}\:{tangent} \\ $$$${the}\:{eqn}\:{of}\:{diameter}\:\parallel\:{to}\:\mathrm{2}{x}−{y}=\mathrm{8} \\ $$$${is}\:\mathrm{2}{x}−{y}={k}\:{passing}\:{through}\:{cdntre}\:{of}\:{circle} \\ $$$${so}\:\mathrm{2}×\mathrm{2}−\mathrm{1}={k}\rightarrow{k}=\mathrm{3} \\ $$$${so}\:{the}\:{reauired}\:{diameter}\:\parallel\:{to}\:\mathrm{2}{x}−{y}=\mathrm{8}\: \\ $$$${is}\:\mathrm{2}{x}−{y}=\mathrm{3} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 28/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 28/May/19
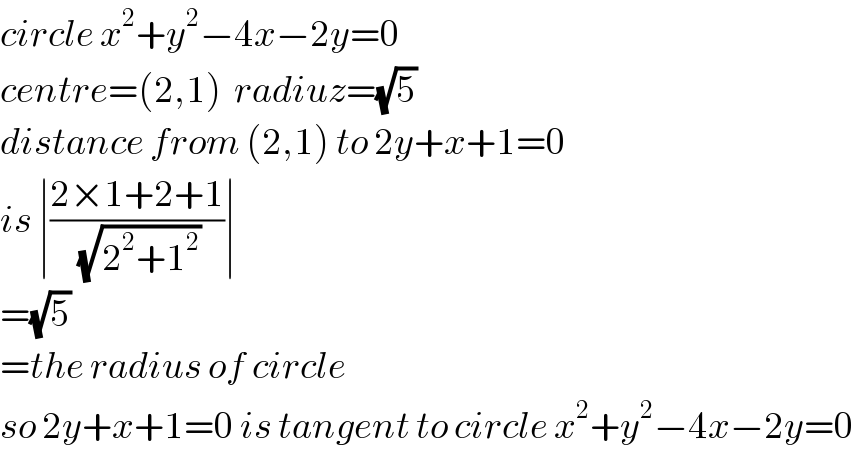
$${circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{2}{y}=\mathrm{0} \\ $$$${centre}=\left(\mathrm{2},\mathrm{1}\right)\:\:{radiuz}=\sqrt{\mathrm{5}}\: \\ $$$${distance}\:{from}\:\left(\mathrm{2},\mathrm{1}\right)\:{to}\:\mathrm{2}{y}+{x}+\mathrm{1}=\mathrm{0} \\ $$$${is}\:\mid\frac{\mathrm{2}×\mathrm{1}+\mathrm{2}+\mathrm{1}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\mid \\ $$$$=\sqrt{\mathrm{5}}\: \\ $$$$={the}\:{radius}\:{of}\:{circle}\: \\ $$$${so}\:\mathrm{2}{y}+{x}+\mathrm{1}=\mathrm{0}\:{is}\:{tangent}\:{to}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{2}{y}=\mathrm{0} \\ $$
Commented by Tawa1 last updated on 28/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
