Question Number 61030 by aanur last updated on 28/May/19
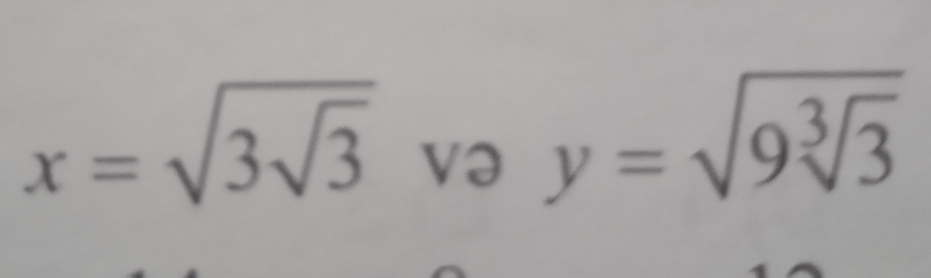
Commented by prakash jain last updated on 28/May/19
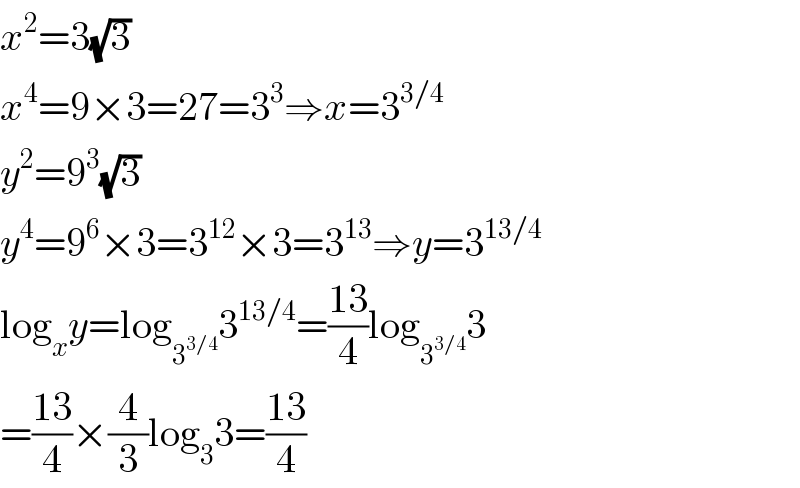
$${x}^{\mathrm{2}} =\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{4}} =\mathrm{9}×\mathrm{3}=\mathrm{27}=\mathrm{3}^{\mathrm{3}} \Rightarrow{x}=\mathrm{3}^{\mathrm{3}/\mathrm{4}} \\ $$$${y}^{\mathrm{2}} =\mathrm{9}^{\mathrm{3}} \sqrt{\mathrm{3}} \\ $$$${y}^{\mathrm{4}} =\mathrm{9}^{\mathrm{6}} ×\mathrm{3}=\mathrm{3}^{\mathrm{12}} ×\mathrm{3}=\mathrm{3}^{\mathrm{13}} \Rightarrow{y}=\mathrm{3}^{\mathrm{13}/\mathrm{4}} \\ $$$$\mathrm{log}_{{x}} {y}=\mathrm{log}_{\mathrm{3}^{\mathrm{3}/\mathrm{4}} } \mathrm{3}^{\mathrm{13}/\mathrm{4}} =\frac{\mathrm{13}}{\mathrm{4}}\mathrm{log}_{\mathrm{3}^{\mathrm{3}/\mathrm{4}} } \mathrm{3} \\ $$$$=\frac{\mathrm{13}}{\mathrm{4}}×\frac{\mathrm{4}}{\mathrm{3}}\mathrm{log}_{\mathrm{3}} \mathrm{3}=\frac{\mathrm{13}}{\mathrm{4}} \\ $$
Commented by aanur last updated on 28/May/19
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
