Question Number 61042 by aliesam last updated on 28/May/19

Answered by ajfour last updated on 28/May/19
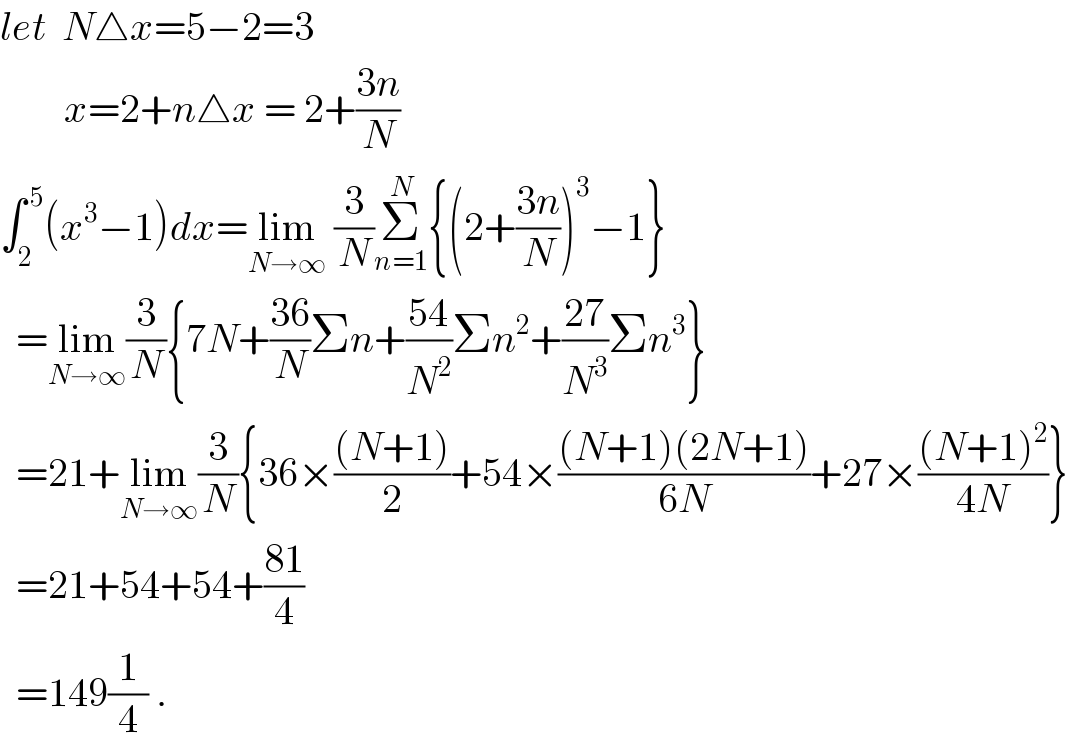
$${let}\:\:{N}\bigtriangleup{x}=\mathrm{5}−\mathrm{2}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{2}+{n}\bigtriangleup{x}\:=\:\mathrm{2}+\frac{\mathrm{3}{n}}{{N}} \\ $$$$\int_{\mathrm{2}} ^{\:\mathrm{5}} \left({x}^{\mathrm{3}} −\mathrm{1}\right){dx}=\underset{{N}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}}{{N}}\underset{{n}=\mathrm{1}} {\overset{{N}} {\sum}}\left\{\left(\mathrm{2}+\frac{\mathrm{3}{n}}{{N}}\right)^{\mathrm{3}} −\mathrm{1}\right\} \\ $$$$\:\:=\underset{{N}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}}{{N}}\left\{\mathrm{7}{N}+\frac{\mathrm{36}}{{N}}\Sigma{n}+\frac{\mathrm{54}}{{N}^{\mathrm{2}} }\Sigma{n}^{\mathrm{2}} +\frac{\mathrm{27}}{{N}^{\mathrm{3}} }\Sigma{n}^{\mathrm{3}} \right\} \\ $$$$\:\:=\mathrm{21}+\underset{{N}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}}{{N}}\left\{\mathrm{36}×\frac{\left({N}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{54}×\frac{\left({N}+\mathrm{1}\right)\left(\mathrm{2}{N}+\mathrm{1}\right)}{\mathrm{6}{N}}+\mathrm{27}×\frac{\left({N}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{N}}\right\} \\ $$$$\:\:=\mathrm{21}+\mathrm{54}+\mathrm{54}+\frac{\mathrm{81}}{\mathrm{4}} \\ $$$$\:\:=\mathrm{149}\frac{\mathrm{1}}{\mathrm{4}}\:. \\ $$
