Question Number 61112 by Kunal12588 last updated on 29/May/19

Commented by Kunal12588 last updated on 29/May/19
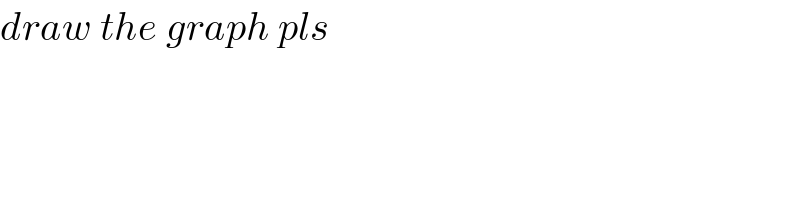
$${draw}\:{the}\:{graph}\:{pls} \\ $$
Commented by Kunal12588 last updated on 29/May/19

Commented by Kunal12588 last updated on 29/May/19
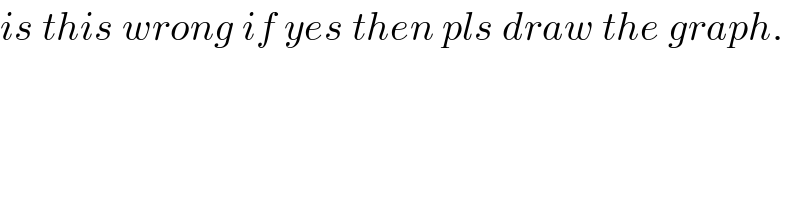
$${is}\:{this}\:{wrong}\:{if}\:{yes}\:{then}\:{pls}\:{draw}\:{the}\:{graph}. \\ $$
Commented by mr W last updated on 29/May/19

$${i}\:{think}\:{your}\:{graph}\:{is}\:{not}\:{correct}. \\ $$$${it}'{s}\:{more}\:{challenging}\:{to}\:{draw}\:{the} \\ $$$${s}−{t},\:{v}−{t}\:{and}\:{a}−{t}\:{graphs}. \\ $$
Answered by tanmay last updated on 29/May/19
![a=(dv/dt)=(dv/ds)×(ds/dt)=v×(dv/ds) upto s=100 meter →(dv/ds)=m=tanθ=((40−0)/(100−0))=(2/5) eqn of v−s graph upto s=100 v=(2/5)×s →[y=mx ] so when s=50 v=(2/5)×50=20 a=v×(dv/ds)=20×(2/5)=8m/sec^2 eqn v−s graph when s∈[100,200] using (y−y_1 )=((y_2 −y_1 )/(x_2 −x_1 ))(x−x_1 ) (100,40) and (200,50) [x→s y→v] v−40=((50−40)/(200−100))(s−100) v=40+(1/(10))(s−100)→so slope=(dv/ds)=(1/(10)) v=40+(1/(10))(150−100) v=45 a=v×(dv/ds) =45×(1/(10))=4.5m/sec^2 pls check... now when s=50 a=8 ehen s=150 a=4.5 so a−s will be a straight line s→along x axis a→along y axis eqn→ using (y−y_1 )=((y_2 −y_1 )/(x_2 −x_1 ))(x−x_1 ) (a−8)=((4.5−8)/(150−50))(s−50) a−8=((3.5)/(100))(s−50) a=0.035s+8−((3.5)/2) a=0.035s+6.25](https://www.tinkutara.com/question/Q61118.png)
$${a}=\frac{{dv}}{{dt}}=\frac{{dv}}{{ds}}×\frac{{ds}}{{dt}}={v}×\frac{{dv}}{{ds}} \\ $$$${upto}\:{s}=\mathrm{100}\:{meter}\:\:\rightarrow\frac{{dv}}{{ds}}={m}={tan}\theta=\frac{\mathrm{40}−\mathrm{0}}{\mathrm{100}−\mathrm{0}}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${eqn}\:{of}\:{v}−{s}\:{graph}\:{upto}\:{s}=\mathrm{100} \\ $$$${v}=\frac{\mathrm{2}}{\mathrm{5}}×{s}\:\:\:\rightarrow\left[{y}={mx}\:\right] \\ $$$${so}\:{when}\:{s}=\mathrm{50}\:\:\:\:\:\:\:\:\:\:{v}=\frac{\mathrm{2}}{\mathrm{5}}×\mathrm{50}=\mathrm{20} \\ $$$${a}={v}×\frac{{dv}}{{ds}}=\mathrm{20}×\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{8}{m}/{sec}^{\mathrm{2}} \\ $$$${eqn}\:{v}−{s}\:{graph}\:{when}\:{s}\in\left[\mathrm{100},\mathrm{200}\right] \\ $$$${using}\:\left({y}−{y}_{\mathrm{1}} \right)=\frac{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }\left({x}−{x}_{\mathrm{1}} \right) \\ $$$$\left(\mathrm{100},\mathrm{40}\right)\:{and}\:\left(\mathrm{200},\mathrm{50}\right)\:\:\left[{x}\rightarrow{s}\:\:\:\:\:{y}\rightarrow{v}\right] \\ $$$${v}−\mathrm{40}=\frac{\mathrm{50}−\mathrm{40}}{\mathrm{200}−\mathrm{100}}\left({s}−\mathrm{100}\right) \\ $$$${v}=\mathrm{40}+\frac{\mathrm{1}}{\mathrm{10}}\left({s}−\mathrm{100}\right)\rightarrow{so}\:{slope}=\frac{{dv}}{{ds}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${v}=\mathrm{40}+\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{150}−\mathrm{100}\right) \\ $$$${v}=\mathrm{45} \\ $$$${a}={v}×\frac{{dv}}{{ds}} \\ $$$$=\mathrm{45}×\frac{\mathrm{1}}{\mathrm{10}}=\mathrm{4}.\mathrm{5}{m}/{sec}^{\mathrm{2}} \\ $$$${pls}\:{check}… \\ $$$${now}\:{when}\:{s}=\mathrm{50}\:\:\:\:\:\:\:{a}=\mathrm{8} \\ $$$${ehen}\:\:\:{s}=\mathrm{150}\:\:\:\:{a}=\mathrm{4}.\mathrm{5} \\ $$$${so}\:{a}−{s}\:{will}\:{be}\:{a}\:{straight}\:{line} \\ $$$${s}\rightarrow{along}\:{x}\:{axis}\:\:\:\:\:{a}\rightarrow{along}\:{y}\:{axis} \\ $$$${eqn}\rightarrow\:{using}\:\left({y}−{y}_{\mathrm{1}} \right)=\frac{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }\left({x}−{x}_{\mathrm{1}} \right) \\ $$$$\left({a}−\mathrm{8}\right)=\frac{\mathrm{4}.\mathrm{5}−\mathrm{8}}{\mathrm{150}−\mathrm{50}}\left({s}−\mathrm{50}\right) \\ $$$${a}−\mathrm{8}=\frac{\mathrm{3}.\mathrm{5}}{\mathrm{100}}\left({s}−\mathrm{50}\right) \\ $$$${a}=\mathrm{0}.\mathrm{035}{s}+\mathrm{8}−\frac{\mathrm{3}.\mathrm{5}}{\mathrm{2}} \\ $$$${a}=\mathrm{0}.\mathrm{035}{s}+\mathrm{6}.\mathrm{25} \\ $$
Commented by Kunal12588 last updated on 29/May/19

Commented by Kunal12588 last updated on 29/May/19
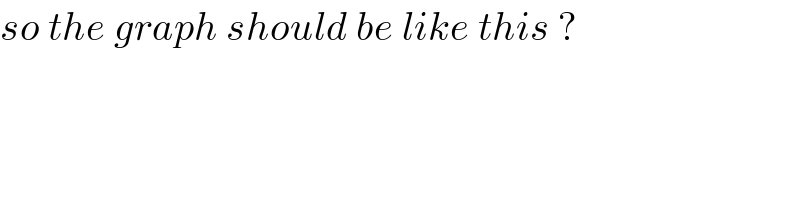
$${so}\:{the}\:{graph}\:{should}\:{be}\:{like}\:{this}\:? \\ $$
Commented by tanmay last updated on 29/May/19

Commented by tanmay last updated on 29/May/19

$${yes}\:{i}\:{am}\:{in}\:{telegram} \\ $$
Commented by Kunal12588 last updated on 29/May/19
https://t.me/kunal1234523
Answered by mr W last updated on 30/May/19
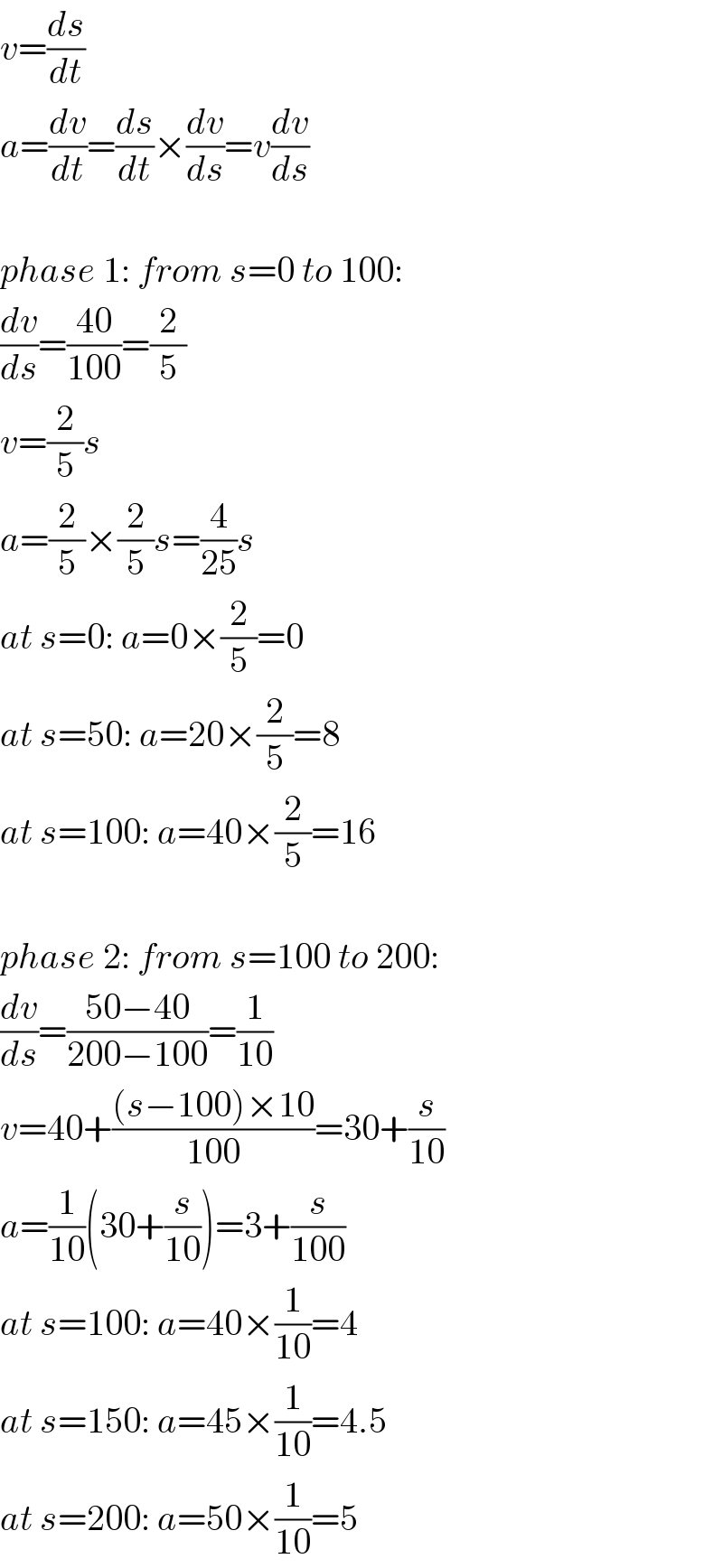
$${v}=\frac{{ds}}{{dt}} \\ $$$${a}=\frac{{dv}}{{dt}}=\frac{{ds}}{{dt}}×\frac{{dv}}{{ds}}={v}\frac{{dv}}{{ds}} \\ $$$$ \\ $$$${phase}\:\mathrm{1}:\:{from}\:{s}=\mathrm{0}\:{to}\:\mathrm{100}: \\ $$$$\frac{{dv}}{{ds}}=\frac{\mathrm{40}}{\mathrm{100}}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${v}=\frac{\mathrm{2}}{\mathrm{5}}{s} \\ $$$${a}=\frac{\mathrm{2}}{\mathrm{5}}×\frac{\mathrm{2}}{\mathrm{5}}{s}=\frac{\mathrm{4}}{\mathrm{25}}{s} \\ $$$${at}\:{s}=\mathrm{0}:\:{a}=\mathrm{0}×\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{0} \\ $$$${at}\:{s}=\mathrm{50}:\:{a}=\mathrm{20}×\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{8} \\ $$$${at}\:{s}=\mathrm{100}:\:{a}=\mathrm{40}×\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{16} \\ $$$$ \\ $$$${phase}\:\mathrm{2}:\:{from}\:{s}=\mathrm{100}\:{to}\:\mathrm{200}: \\ $$$$\frac{{dv}}{{ds}}=\frac{\mathrm{50}−\mathrm{40}}{\mathrm{200}−\mathrm{100}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${v}=\mathrm{40}+\frac{\left({s}−\mathrm{100}\right)×\mathrm{10}}{\mathrm{100}}=\mathrm{30}+\frac{{s}}{\mathrm{10}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{30}+\frac{{s}}{\mathrm{10}}\right)=\mathrm{3}+\frac{{s}}{\mathrm{100}} \\ $$$${at}\:{s}=\mathrm{100}:\:{a}=\mathrm{40}×\frac{\mathrm{1}}{\mathrm{10}}=\mathrm{4} \\ $$$${at}\:{s}=\mathrm{150}:\:{a}=\mathrm{45}×\frac{\mathrm{1}}{\mathrm{10}}=\mathrm{4}.\mathrm{5} \\ $$$${at}\:{s}=\mathrm{200}:\:{a}=\mathrm{50}×\frac{\mathrm{1}}{\mathrm{10}}=\mathrm{5} \\ $$
Commented by mr W last updated on 29/May/19

Commented by mr W last updated on 29/May/19

$${in}\:{phase}\:\mathrm{1}\:{the}\:{force}\:{applied}\:{on}\:{the} \\ $$$${object}\:{is}\:{increased}\:{gradually}.\:{at} \\ $$$${s}=\mathrm{100},\:{an}\:{impact}\:{is}\:{apllied}\:{on}\:{the} \\ $$$${object}\:{in}\:{inversed}\:{direction}.\:{after} \\ $$$${that}\:{in}\:{phase}\:\mathrm{2}\:{the}\:{force}\:{applied}\:{on} \\ $$$${the}\:{object}\:{is}\:{increased}\:{again}\:{gradually}. \\ $$
Commented by Kunal12588 last updated on 30/May/19
![thank you sir so my first phase for s∈[0,100] was correct.](https://www.tinkutara.com/question/Q61188.png)
$${thank}\:{you}\:{sir} \\ $$$${so}\:{my}\:{first}\:{phase}\:{for}\:{s}\in\left[\mathrm{0},\mathrm{100}\right]\:{was}\:{correct}. \\ $$
Commented by Kunal12588 last updated on 30/May/19
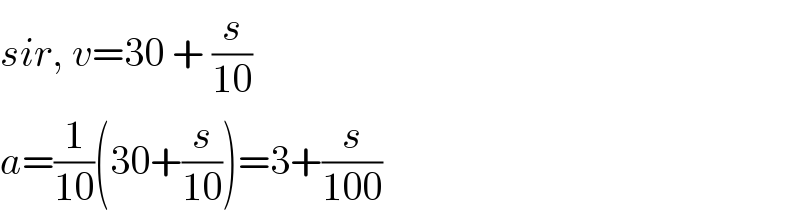
$${sir},\:{v}=\mathrm{30}\:+\:\frac{{s}}{\mathrm{10}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{30}+\frac{{s}}{\mathrm{10}}\right)=\mathrm{3}+\frac{{s}}{\mathrm{100}} \\ $$
Commented by mr W last updated on 30/May/19

$${yes}. \\ $$$${thanks}. \\ $$
