Question-61169

Facebook Tweet Pin

Question Number 61169 by Tawa1 last updated on 29/May/19

Commented by Tawa1 last updated on 29/May/19

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{Black} \\ $$

Answered by mr W last updated on 30/May/19

Commented by mr W last updated on 30/May/19

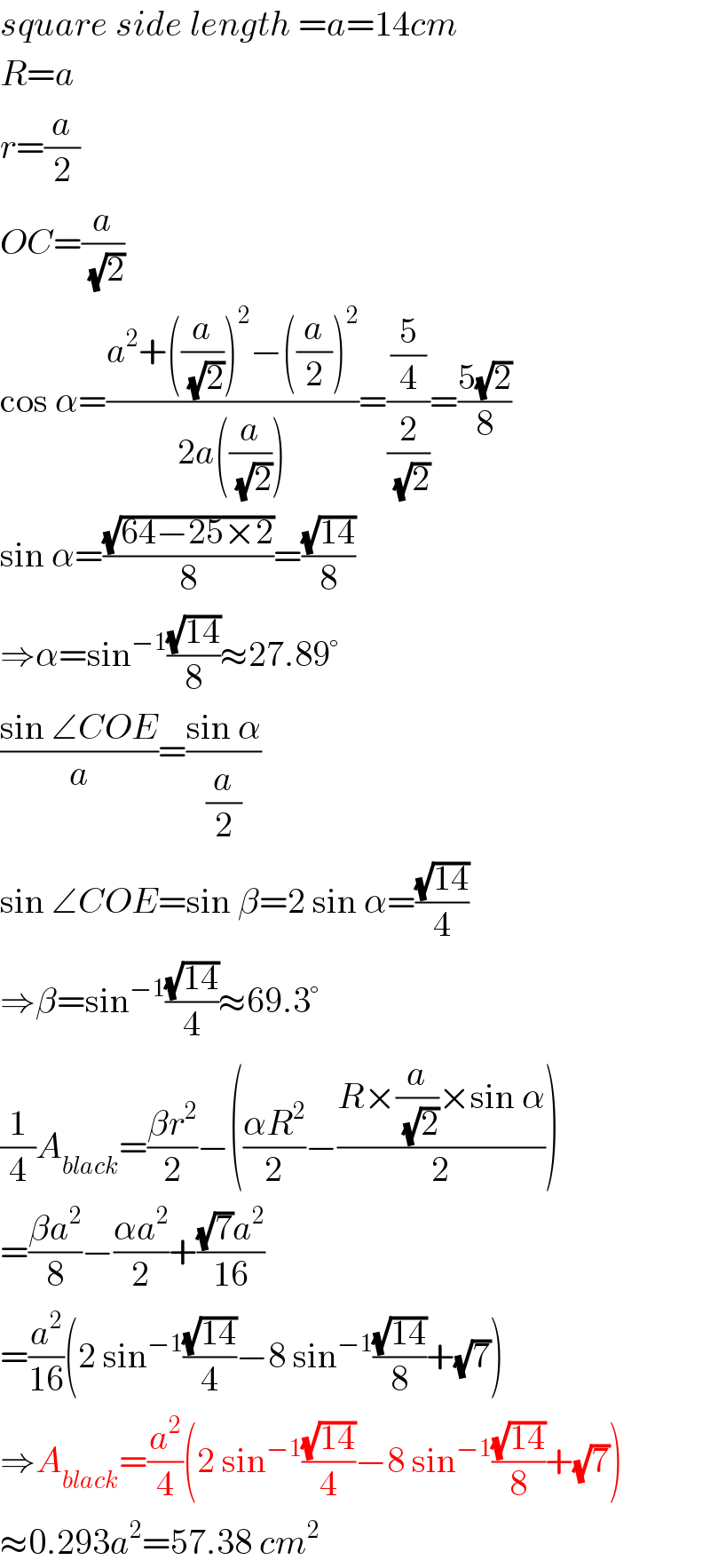
square side length =a=14cm R=a r=(a/2) OC=(a/( (√2))) cos α=((a^2 +((a/( (√2))))^2 −((a/2))^2 )/(2a((a/( (√2))))))=((5/4)/(2/( (√2))))=((5(√2))/8) sin α=((√(64−25×2))/8)=((√(14))/8) ⇒α=sin^(−1) ((√(14))/8)≈27.89° ((sin ∠COE)/a)=((sin α)/(a/2)) sin ∠COE=sin β=2 sin α=((√(14))/4) ⇒β=sin^(−1) ((√(14))/4)≈69.3° (1/4)A_(black) =((βr^2 )/2)−(((αR^2 )/2)−((R×(a/( (√2)))×sin α)/2)) =((βa^2 )/8)−((αa^2 )/2)+(((√7)a^2 )/(16)) =(a^2 /(16))(2 sin^(−1) ((√(14))/4)−8 sin^(−1) ((√(14))/8)+(√7)) ⇒A_(black) =(a^2 /4)(2 sin^(−1) ((√(14))/4)−8 sin^(−1) ((√(14))/8)+(√7)) ≈0.293a^2 =57.38 cm^2

$${square}\:{side}\:{length}\:={a}=\mathrm{14}{cm} \\ $$$${R}={a} \\ $$$${r}=\frac{{a}}{\mathrm{2}} \\ $$$${OC}=\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}^{\mathrm{2}} +\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}{a}\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)}=\frac{\frac{\mathrm{5}}{\mathrm{4}}}{\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{64}−\mathrm{25}×\mathrm{2}}}{\mathrm{8}}=\frac{\sqrt{\mathrm{14}}}{\mathrm{8}} \\ $$$$\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{8}}\approx\mathrm{27}.\mathrm{89}° \\ $$$$\frac{\mathrm{sin}\:\angle{COE}}{{a}}=\frac{\mathrm{sin}\:\alpha}{\frac{{a}}{\mathrm{2}}} \\ $$$$\mathrm{sin}\:\angle{COE}=\mathrm{sin}\:\beta=\mathrm{2}\:\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{14}}}{\mathrm{4}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\approx\mathrm{69}.\mathrm{3}° \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{A}_{{black}} =\frac{\beta{r}^{\mathrm{2}} }{\mathrm{2}}−\left(\frac{\alpha{R}^{\mathrm{2}} }{\mathrm{2}}−\frac{{R}×\frac{{a}}{\:\sqrt{\mathrm{2}}}×\mathrm{sin}\:\alpha}{\mathrm{2}}\right) \\ $$$$=\frac{\beta{a}^{\mathrm{2}} }{\mathrm{8}}−\frac{\alpha{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}{a}^{\mathrm{2}} }{\mathrm{16}} \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{16}}\left(\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}}−\mathrm{8}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{8}}+\sqrt{\mathrm{7}}\right) \\ $$$$\Rightarrow{A}_{{black}} =\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}}−\mathrm{8}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{8}}+\sqrt{\mathrm{7}}\right) \\ $$$$\approx\mathrm{0}.\mathrm{293}{a}^{\mathrm{2}} =\mathrm{57}.\mathrm{38}\:{cm}^{\mathrm{2}} \\ $$

Commented by Tawa1 last updated on 30/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$

Commented by Tawa1 last updated on 30/May/19

Sir, any basis to learn all this shapes ?. I want to start learning it from the begining

$$\mathrm{Sir},\:\mathrm{any}\:\mathrm{basis}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{all}\:\mathrm{this}\:\mathrm{shapes}\:?.\:\:\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{start}\:\mathrm{learning} \\ $$$$\mathrm{it}\:\mathrm{from}\:\mathrm{the}\:\mathrm{begining} \\ $$

Commented by mr W last updated on 30/May/19

$${sorry}\:{i}\:{can}'{t}\:{answer}\:{your}\:{question}, \\ $$$${because}\:{i}\:{don}'{t}\:{know}\:{what}\:{have}\:{already} \\ $$$${learnt}\:{and}\:{what}\:{not}\:{yet}.\:{according}\:{to} \\ $$$${the}\:{questions}\:{you}\:{put}\:{here},\:{i}\:{think}, \\ $$$${you}\:{have}\:{all}\:{the}\:{knowledge}\:{which}\:{is} \\ $$$${necessary}\:{to}\:{solve}\:{such}\:{questions}. \\ $$

Commented by Tawa1 last updated on 30/May/19