Question Number 61186 by Tawa1 last updated on 30/May/19

Commented by Prithwish sen last updated on 30/May/19
![Area of the shadded portion =Area of the incircle −Area of the quarter circle +(3/4)(Area of the square −Area of the incircle) =π5^2 −(1/4)π(10)^2 +(3/4)[(10)^2 −π5^2 ] =(1/4)π5^2 −(1/4)π10^2 +(3/4)10^2 =(3/4)×100 −(π/4)×75 ∽16.09 please check the answer](https://www.tinkutara.com/question/Q61190.png)
$$\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shadded}\:\mathrm{portion}\:=\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{incircle}\: \\ $$$$−\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quarter}\:\mathrm{circle}\:+\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\right. \\ $$$$\left.\mathrm{square}\:−\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{incircle}\right) \\ $$$$=\pi\mathrm{5}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\left(\mathrm{10}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\left[\left(\mathrm{10}\right)^{\mathrm{2}} −\pi\mathrm{5}^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\pi\mathrm{5}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\pi\mathrm{10}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\mathrm{10}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{100}\:−\frac{\pi}{\mathrm{4}}×\mathrm{75}\:\backsim\mathrm{16}.\mathrm{09} \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{the}\:\mathrm{answer} \\ $$
Commented by mr W last updated on 30/May/19
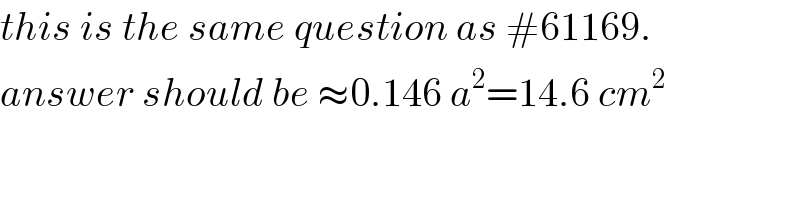
$${this}\:{is}\:{the}\:{same}\:{question}\:{as}\:#\mathrm{61169}. \\ $$$${answer}\:{should}\:{be}\:\approx\mathrm{0}.\mathrm{146}\:{a}^{\mathrm{2}} =\mathrm{14}.\mathrm{6}\:{cm}^{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 30/May/19
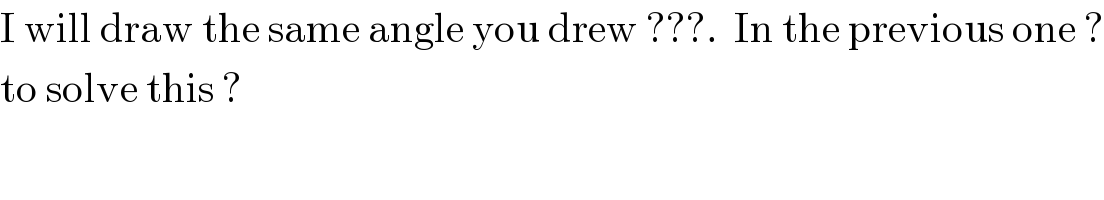
$$\mathrm{I}\:\mathrm{will}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{same}\:\mathrm{angle}\:\mathrm{you}\:\mathrm{drew}\:???.\:\:\mathrm{In}\:\mathrm{the}\:\mathrm{previous}\:\mathrm{one}\:? \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:? \\ $$
