Question-61208

Question Number 61208 by Tawa1 last updated on 30/May/19

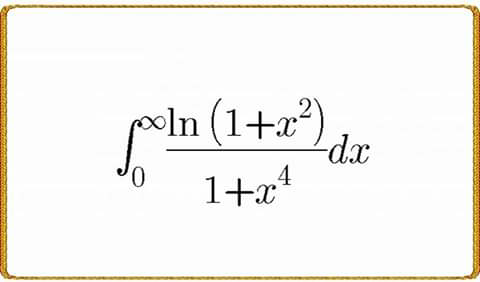
Commented by maxmathsup by imad last updated on 30/May/19

its only a try let f(t) =∫_0 ^∞ ((ln(1+tx^2 ))/(1+x^4 )) dx with t ≥0 we have f^′ (t) =∫_0 ^∞ (x^2 /((1+tx^2 )(1+x^4 ))) dx ⇒2f^′ (t) =∫_(−∞) ^(+∞) (x^2 /((1+tx^2 )(1+x^4 )))dx let consider the complex function ϕ(z) =(z^2 /((tz^2 +1)(z^4 +1))) poles of ϕ? we have ϕ(z) =(z^2 /(((√t)z+i)((√t)z −i)(z^2 −i)(z^2 +i))) =(z^2 /(t(z+(i/( (√t))))(z−(i/( (√t))))(z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) (t>0) so the poles of ϕ are +^− (i/( (√( t)))) ,+^− e^((iπ)/4) , +^− e^(−((iπ)/4)) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,(i/( (√t)))) +Res(ϕ,e^((iπ)/4) ) +Res(ϕ,−e^(−((iπ)/4)) )} the poles are simples so Res(ϕ,(i/( (√t)))) =lim_(z→(i/( (√t)))) (z−(i/( (√t))))ϕ(z)=((−1)/(t^2 (((2i)/( (√t))))(1+(1/t^2 )))) =((−(√t))/(2i(t^2 +1))) Res(ϕ,e^((iπ)/4) ) =lim_(z→e^((iπ)/4) ) (z−e^((iπ)/4) )ϕ(z)=(i/((ti+1)(2e^((iπ)/4) )(2i))) = (e^(−((iπ)/4)) /(4(1+it))) Res(ϕ,−e^(−((iπ)/4)) ) =((−i)/((1−it)(−2i)(−2 e^(−((iπ)/4)) ))) =−(e^((iπ)/4) /(4(1−it))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ ((−(√t))/(2i(t^2 +1))) +(e^(−((iπ)/4)) /(4(1+it))) −(e^((iπ)/4) /(4(1−it)))} =((−π(√t))/(t^2 +1)) +((iπ)/2) {− 2iIm((e^((iπ)/4) /(1−it)))} but (e^((iπ)/4) /(1−it)) =(((1+it)((1/( (√2))) +(i/( (√2)))))/(1+t^2 )) =(((1+it)(1+i))/( (√2)(t^2 +1))) =((1+i+it−t)/( (√2)(t^2 +1))) =((1−t +(t+1)i)/( (√2)(t^2 +1))) ⇒ Im((e^((iπ)/4) /(1−it))) =((1+t)/( (√2)(t^2 +1))) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =((−π(√t))/(t^2 +1)) +((π(1+t))/(t^2 +1)) =((−π(√t) +π +πt)/(t^2 +1)) =2f^′ (t) ⇒ f(t) = (1/2) ∫_0 ^t ((πx−π(√x) +π)/(x^2 +1)) dt +λ ∫_0 ^t ((πx−π(√x) +π)/(x^2 +1)) dt =(π/2)ln(t^2 +1) +(π/2) arctan(t)−(π/2) ∫_0 ^t ((√x)/(x^2 +1)) dt ∫_0 ^t ((√x)/(x^2 +1)) dt =_((√x)=u) ∫_0 ^(√t) (u/(u^4 +1)) (2u)du =2 ∫_0 ^(√t) (u^2 /(u^4 +1)) du ⇒ f(t) =(π/2)ln(1+t^2 )+(π/2) arctan(t)−π ∫_0 ^(√t) (u^2 /(1+u^4 )) du (λ =f(0)=0) ⇒∫_0 ^∞ ((ln(1+x^2 ))/(1+x^4 )) dx =f(1)= (π/2)ln(2) +(π^2 /8) −π ∫_0 ^1 (u^2 /(1+u^4 )) du

$${its}\:{only}\:{a}\:{try}\:{let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\:\:{with}\:{t}\:\geqslant\mathrm{0} \\ $$$${we}\:{have}\:{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:{dx}\:\Rightarrow\mathrm{2}{f}^{'} \left({t}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}{dx} \\ $$$${let}\:{consider}\:{the}\:{complex}\:{function}\:\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({tz}^{\mathrm{2}} +\mathrm{1}\right)\left({z}^{\mathrm{4}} \:+\mathrm{1}\right)} \\ $$$${poles}\:{of}\:\varphi?\:\:\:{we}\:{have}\:\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left(\sqrt{{t}}{z}+{i}\right)\left(\sqrt{{t}}{z}\:−{i}\right)\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)} \\ $$$$=\frac{{z}^{\mathrm{2}} }{{t}\left({z}+\frac{{i}}{\:\sqrt{{t}}}\right)\left({z}−\frac{{i}}{\:\sqrt{{t}}}\right)\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:\:\:\left({t}>\mathrm{0}\right) \\ $$$${so}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}\frac{{i}}{\:\sqrt{\:{t}}}\:\:,\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:,\:\overset{−} {+}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,\frac{{i}}{\:\sqrt{{t}}}\right)\:+{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${the}\:{poles}\:{are}\:{simples}\:{so} \\ $$$${Res}\left(\varphi,\frac{{i}}{\:\sqrt{{t}}}\right)\:={lim}_{{z}\rightarrow\frac{{i}}{\:\sqrt{{t}}}} \:\left({z}−\frac{{i}}{\:\sqrt{{t}}}\right)\varphi\left({z}\right)=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} \left(\frac{\mathrm{2}{i}}{\:\sqrt{{t}}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)}\:=\frac{−\sqrt{{t}}}{\mathrm{2}{i}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\varphi\left({z}\right)=\frac{{i}}{\left({ti}+\mathrm{1}\right)\left(\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{2}{i}\right)} \\ $$$$=\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}\left(\mathrm{1}+{it}\right)} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{−{i}}{\left(\mathrm{1}−{it}\right)\left(−\mathrm{2}{i}\right)\left(−\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=−\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}\left(\mathrm{1}−{it}\right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\frac{−\sqrt{{t}}}{\mathrm{2}{i}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}\left(\mathrm{1}+{it}\right)}\:−\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}\left(\mathrm{1}−{it}\right)}\right\} \\ $$$$=\frac{−\pi\sqrt{{t}}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{i}\pi}{\mathrm{2}}\:\left\{−\:\mathrm{2}{iIm}\left(\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{1}−{it}}\right)\right\}\:\:{but}\:\:\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{1}−{it}}\:=\frac{\left(\mathrm{1}+{it}\right)\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{1}+{it}\right)\left(\mathrm{1}+{i}\right)}{\:\sqrt{\mathrm{2}}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}+{i}+{it}−{t}}{\:\sqrt{\mathrm{2}}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}−{t}\:+\left({t}+\mathrm{1}\right){i}}{\:\sqrt{\mathrm{2}}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${Im}\left(\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{1}−{it}}\right)\:=\frac{\mathrm{1}+{t}}{\:\sqrt{\mathrm{2}}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{−\pi\sqrt{{t}}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\pi\left(\mathrm{1}+{t}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{−\pi\sqrt{{t}}\:+\pi\:+\pi{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{2}{f}^{'} \left({t}\right)\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{\pi{x}−\pi\sqrt{{x}}\:+\pi}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:\:+\lambda \\ $$$$\int_{\mathrm{0}} ^{{t}} \:\:\frac{\pi{x}−\pi\sqrt{{x}}\:+\pi}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\frac{\pi}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\frac{\pi}{\mathrm{2}}\:{arctan}\left({t}\right)−\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{t}} \:\frac{\sqrt{{x}}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dt} \\ $$$$\int_{\mathrm{0}} ^{{t}} \:\:\frac{\sqrt{{x}}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=_{\sqrt{{x}}={u}} \:\:\:\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\:\:\:\frac{{u}}{{u}^{\mathrm{4}} \:+\mathrm{1}}\:\left(\mathrm{2}{u}\right){du}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\:\:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} \:+\mathrm{1}}\:{du}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\frac{\pi}{\mathrm{2}}\:{arctan}\left({t}\right)−\pi\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \frac{{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{4}} }\:{du}\: \\ $$$$\left(\lambda\:={f}\left(\mathrm{0}\right)=\mathrm{0}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\:={f}\left(\mathrm{1}\right)= \\ $$$$\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\pi\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{4}} }\:{du} \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 30/May/19

let decompose F(u) =(u^2 /(u^4 +1)) ⇒F(u) =(u^2 /((u^2 +1)^2 −2u^2 )) =(u^2 /((u^2 +(√2)u +1)(u^2 −(√2)u +1))) =((au +b)/(u^2 +(√2)u +1)) +((cu +d)/(u^2 −(√2)u +1)) F(−u) =F(u) ⇒((−au +b)/(u^2 −(√2)u +1)) +((−cu +d)/(u^2 +(√2)u +1)) =F(u) ⇒c=−a and b=d ⇒F(u) =((au +b)/(u^2 +(√2)u +1)) +((−au +b)/(u^2 −(√2)u +1)) F(0) =0 =2b ⇒b=0 F(1) =(1/2) = (a/(2+(√2))) −(a/(2−(√2))) =(((2−(√2)−2−(√2))a)/2) ⇒1=−2(√2)a ⇒ a =−(1/(2(√2))) ⇒F(u) =−(1/(2(√2))) (u/(u^2 +(√2)u +1)) +(1/(2(√2))) (u/(u^2 −(√2)u +1)) ⇒ ∫_0 ^1 F(u)du =−(1/(4(√2))) ∫_0 ^1 ((2u+(√2)−(√2))/(u^2 +(√2)u +1)) du +(1/(4(√2))) ∫_0 ^1 ((2u−(√2) +(√2))/(u^2 −(√2) u +1))du =−(1/(4(√2)))[ln(u^2 +(√2)u +1)]_0 ^1 +(1/4) ∫_0 ^1 (du/(u^2 +(√2)u +1)) +(1/(4(√2)))[ln(u^2 −(√2)u +1)]_0 ^1 +(1/4) ∫_0 ^1 (du/(u^2 −(√2)u +1)) ∫_0 ^1 (du/(u^2 +(√2)u +1)) =∫_0 ^1 (du/(u^2 +2(1/( (√2)))u +(1/2) +(1/2))) =∫_0 ^1 (du/((u+(1/( (√2))))^2 +(1/2))) =_(u+(1/( (√2)))=(t/( (√2)))) ∫_1 ^((√2) +1) (dt/( (√2)((1/2))(1+t^2 ))) =(√2) [arctan(t)]_1 ^((√2) +1) =(√2){ arctan(1+(√2))−(π/4)} ∫_0 ^1 (du/(u^2 −(√2)u +1)) =∫_0 ^1 (du/((u−(1/( (√2))))^2 +(1/2))) =_(u−(1/( (√2)))=(t/( (√2)))) ∫_(−1) ^((√2)−1) (dt/( (√2)((1/2))(1+t^2 ))) =(√2) [arctan(t)]_(−1) ^((√2)−1) =(√2){ arctan((√2)−1)+(π/4)} ⇒ ∫_0 ^1 F(u)du =−(1/(4(√2)))ln(2+(√2)) +(1/(4(√2)))ln(2−(√2))+((√2)/4){arctan(1+(√2))−(π/4)} +((√2)/4){arctan((√2)−1)−(π/4)} ⇒ ∫_0 ^∞ ((ln(1+x^2 ))/(1+x^4 )) dx =(π/2)ln(2)+(π^2 /8) +(π/(4(√2))){ln(((2−(√2))/(2+(√2))))} −π((√2)/4){ arctan((√2) +1) +arctan((√2) −1)−(π/2)} .

$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$=\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}\:+\mathrm{1}\right)\left({u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}\right)}\:=\frac{{au}\:+{b}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}} \\ $$$${F}\left(−{u}\right)\:={F}\left({u}\right)\:\Rightarrow\frac{−{au}\:+{b}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:+\frac{−{cu}\:+{d}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:={F}\left({u}\right)\:\Rightarrow{c}=−{a}\:{and}\: \\ $$$${b}={d}\:\Rightarrow{F}\left({u}\right)\:=\frac{{au}\:+{b}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:+\frac{−{au}\:+{b}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\mathrm{2}{b}\:\Rightarrow{b}=\mathrm{0}\: \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{{a}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:−\frac{{a}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}−\mathrm{2}−\sqrt{\mathrm{2}}\right){a}}{\mathrm{2}}\:\Rightarrow\mathrm{1}=−\mathrm{2}\sqrt{\mathrm{2}}{a}\:\Rightarrow \\ $$$${a}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow{F}\left({u}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{{u}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{{u}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({u}\right){du}\:\:=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:{du}\:+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{u}−\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}\:{u}\:+\mathrm{1}}{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[{ln}\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}\:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{u}\:+\mathrm{1}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[{ln}\left({u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{u}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{\left({u}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=_{{u}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{{t}}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}\:+\mathrm{1}} \:\:\:\:\:\frac{{dt}}{\:\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:=\sqrt{\mathrm{2}}\:\left[{arctan}\left({t}\right)\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}\:+\mathrm{1}} \\ $$$$=\sqrt{\mathrm{2}}\left\{\:{arctan}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{du}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}\:+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{du}}{\left({u}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}}\:=_{{u}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{{t}}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\int_{−\mathrm{1}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{dt}}{\:\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\sqrt{\mathrm{2}}\:\left[{arctan}\left({t}\right)\right]_{−\mathrm{1}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:=\sqrt{\mathrm{2}}\left\{\:{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\frac{\pi}{\mathrm{4}}\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({u}\right){du}\:=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left\{{arctan}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left\{{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)−\frac{\pi}{\mathrm{4}}\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$−\pi\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left\{\:{arctan}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\:+{arctan}\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)−\frac{\pi}{\mathrm{2}}\right\}\:. \\ $$$$ \\ $$

Commented by ajfour last updated on 30/May/19