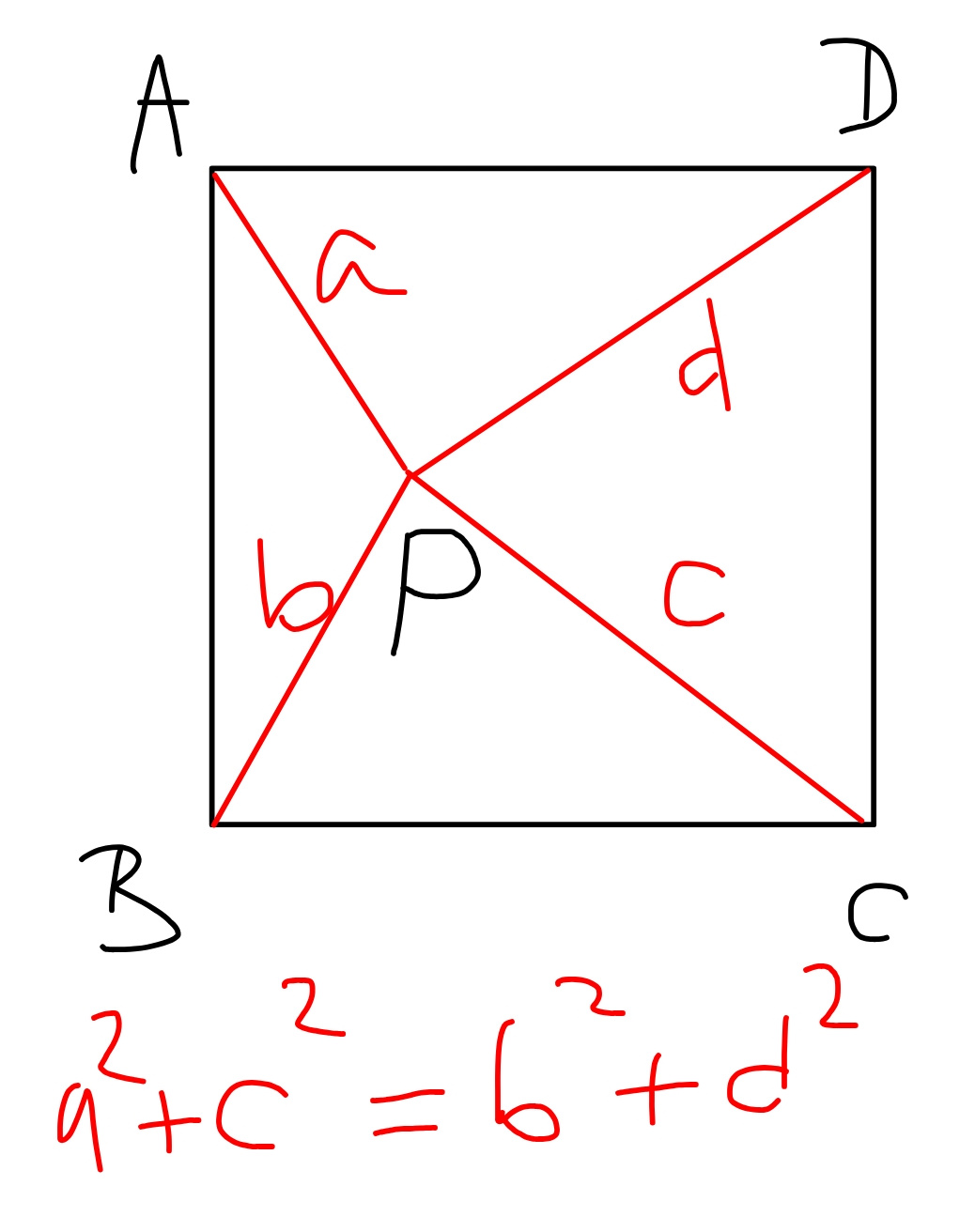
Question Number 61215 by naka3546 last updated on 30/May/19
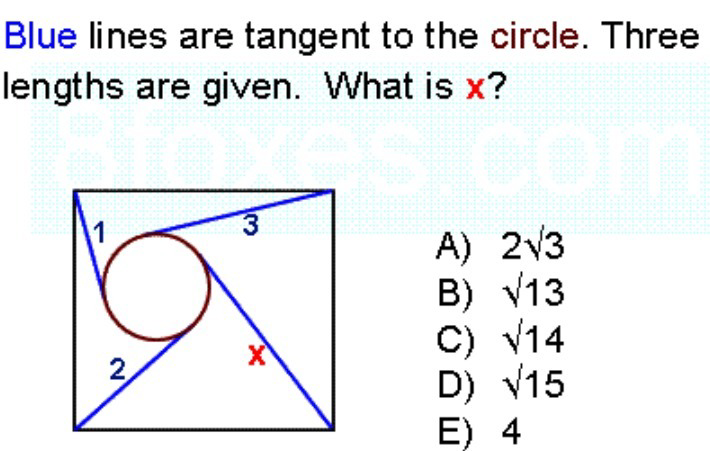
Answered by ajfour last updated on 30/May/19
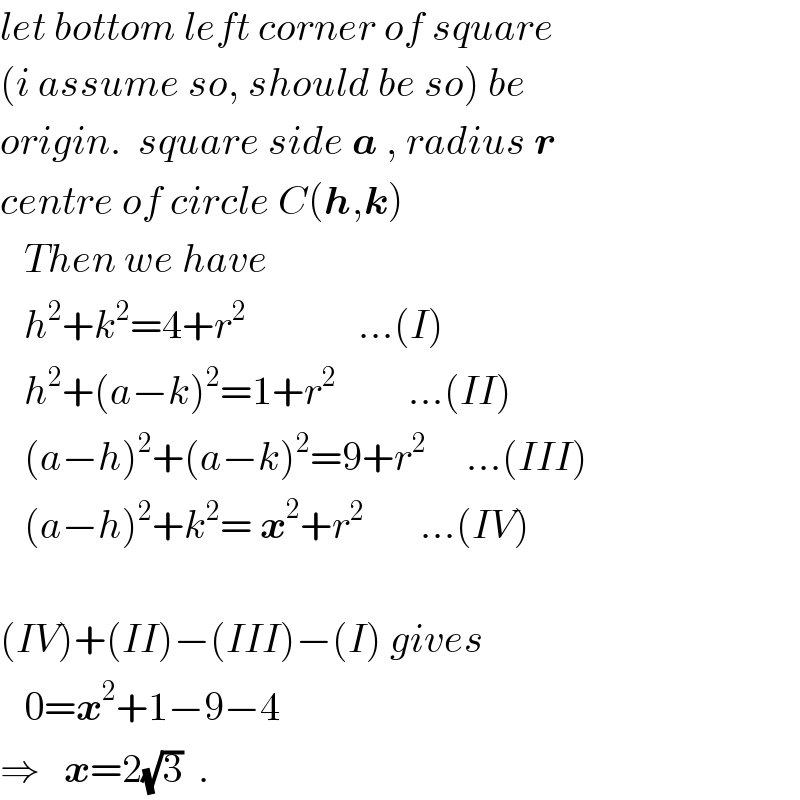
$${let}\:{bottom}\:{left}\:{corner}\:{of}\:{square} \\ $$$$\left({i}\:{assume}\:{so},\:{should}\:{be}\:{so}\right)\:{be} \\ $$$${origin}.\:\:{square}\:{side}\:\boldsymbol{{a}}\:,\:{radius}\:\boldsymbol{{r}} \\ $$$${centre}\:{of}\:{circle}\:{C}\left(\boldsymbol{{h}},\boldsymbol{{k}}\right) \\ $$$$\:\:\:{Then}\:{we}\:{have} \\ $$$$\:\:\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\mathrm{4}+{r}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({I}\right) \\ $$$$\:\:\:{h}^{\mathrm{2}} +\left({a}−{k}\right)^{\mathrm{2}} =\mathrm{1}+{r}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:…\left({II}\right) \\ $$$$\:\:\:\left({a}−{h}\right)^{\mathrm{2}} +\left({a}−{k}\right)^{\mathrm{2}} =\mathrm{9}+{r}^{\mathrm{2}} \:\:\:\:\:…\left({III}\right) \\ $$$$\:\:\:\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\:\boldsymbol{{x}}^{\mathrm{2}} +{r}^{\mathrm{2}} \:\:\:\:\:\:\:…\left({IV}\right) \\ $$$$ \\ $$$$\left({IV}\right)+\left({II}\right)−\left({III}\right)−\left({I}\right)\:{gives} \\ $$$$\:\:\:\mathrm{0}=\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}−\mathrm{9}−\mathrm{4} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{x}}=\mathrm{2}\sqrt{\mathrm{3}}\:\:. \\ $$
Answered by mr W last updated on 30/May/19
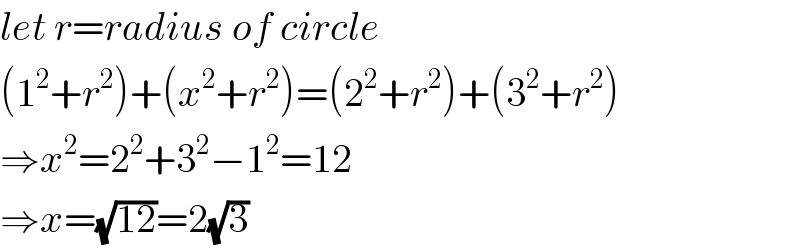
$${let}\:{r}={radius}\:{of}\:{circle} \\ $$$$\left(\mathrm{1}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)+\left({x}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)=\left(\mathrm{2}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)+\left(\mathrm{3}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} =\mathrm{12} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{12}}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by mr W last updated on 30/May/19