Question-61235

Question Number 61235 by ajfour last updated on 30/May/19

Commented by ajfour last updated on 30/May/19

$${Find}\:{h}\:{and}\:{R}\:{of}\:{maximum}\:{volume} \\ $$$$\:{inscribed}\:{cylinder}\:{with}\:{its}\:{base}\:{on} \\ $$$${face}\:{ABC}\:{of}\:{a}\:{general}\:{pyramid}. \\ $$

Commented by mr W last updated on 30/May/19

Area of base A_b : A_b =(1/4)(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))) Volume of pyramid V_p : V_p =(1/(12))(√(Σa^2 p^2 (−a^2 −p^2 +b^2 +q^2 +c^2 +r^2 )−Σa^2 b^2 c^2 )) Height of pyramid H: H=((3V_p )/A_b ) Section triangle at height h: a_1 =(1−(h/H))a b_1 =(1−(h/H))b c_1 =(1−(h/H))c radius of inscribed circle in section: R=((2A_1 )/p_1 ) with A_1 =area of section triangle p_1 =perimeter of section triangle A_1 =(1−(h/H))^2 A_b p_1 =(1−(h/H))p_b with p_b =a+b+c ⇒R=2(1−(h/H))(A_b /p_b ) Volume of inscribed cylinder V_c : V_c =πR^2 h=((4πA_b ^2 )/p_b ^2 )(1−(h/H))^2 h =((4πA_b ^2 H)/p_b ^2 )(1−λ)^2 λ with λ=(h/H) (dV_c /dh)=0 ⇒(1−λ)^2 −2(1−λ)λ=0 ⇒1−3λ=0 ⇒λ=(1/3) i.e. for maximum volume of cylinder h=(H/3)=(V_p /A_b )=(1/3)(√((Σa^2 p^2 (−a^2 −p^2 +b^2 +q^2 +c^2 +r^2 )−Σa^2 b^2 c^2 )/((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))) R=((4A_b )/(3p_b ))=(1/3)(√(((−a+b+c)(a−b+c)(a+b−c))/((a+b+c))))

$${Area}\:{of}\:{base}\:{A}_{{b}} :\: \\ $$$${A}_{{b}} =\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$${Volume}\:{of}\:{pyramid}\:{V}_{{p}} : \\ $$$${V}_{{p}} =\frac{\mathrm{1}}{\mathrm{12}}\sqrt{\Sigma{a}^{\mathrm{2}} {p}^{\mathrm{2}} \left(−{a}^{\mathrm{2}} −{p}^{\mathrm{2}} +{b}^{\mathrm{2}} +{q}^{\mathrm{2}} +{c}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)−\Sigma{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} } \\ $$$${Height}\:{of}\:{pyramid}\:{H}: \\ $$$${H}=\frac{\mathrm{3}{V}_{{p}} }{{A}_{{b}} } \\ $$$${Section}\:{triangle}\:{at}\:{height}\:{h}: \\ $$$${a}_{\mathrm{1}} =\left(\mathrm{1}−\frac{{h}}{{H}}\right){a} \\ $$$${b}_{\mathrm{1}} =\left(\mathrm{1}−\frac{{h}}{{H}}\right){b} \\ $$$${c}_{\mathrm{1}} =\left(\mathrm{1}−\frac{{h}}{{H}}\right){c} \\ $$$${radius}\:{of}\:{inscribed}\:{circle}\:{in}\:{section}: \\ $$$${R}=\frac{\mathrm{2}{A}_{\mathrm{1}} }{{p}_{\mathrm{1}} } \\ $$$${with}\:{A}_{\mathrm{1}} ={area}\:{of}\:{section}\:{triangle} \\ $$$${p}_{\mathrm{1}} ={perimeter}\:{of}\:{section}\:{triangle} \\ $$$${A}_{\mathrm{1}} =\left(\mathrm{1}−\frac{{h}}{{H}}\right)^{\mathrm{2}} {A}_{{b}} \\ $$$${p}_{\mathrm{1}} =\left(\mathrm{1}−\frac{{h}}{{H}}\right){p}_{{b}} \:{with}\:{p}_{{b}} ={a}+{b}+{c} \\ $$$$\Rightarrow{R}=\mathrm{2}\left(\mathrm{1}−\frac{{h}}{{H}}\right)\frac{{A}_{{b}} }{{p}_{{b}} } \\ $$$${Volume}\:{of}\:{inscribed}\:{cylinder}\:{V}_{{c}} : \\ $$$${V}_{{c}} =\pi{R}^{\mathrm{2}} {h}=\frac{\mathrm{4}\pi{A}_{{b}} ^{\mathrm{2}} }{{p}_{{b}} ^{\mathrm{2}} }\left(\mathrm{1}−\frac{{h}}{{H}}\right)^{\mathrm{2}} {h} \\ $$$$=\frac{\mathrm{4}\pi{A}_{{b}} ^{\mathrm{2}} {H}}{{p}_{{b}} ^{\mathrm{2}} }\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \lambda\:{with}\:\lambda=\frac{{h}}{{H}} \\ $$$$\frac{{dV}_{{c}} }{{dh}}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\lambda\right)\lambda=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{3}\lambda=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${i}.{e}.\:{for}\:{maximum}\:{volume}\:{of}\:{cylinder} \\ $$$${h}=\frac{{H}}{\mathrm{3}}=\frac{{V}_{{p}} }{{A}_{{b}} }=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\frac{\Sigma{a}^{\mathrm{2}} {p}^{\mathrm{2}} \left(−{a}^{\mathrm{2}} −{p}^{\mathrm{2}} +{b}^{\mathrm{2}} +{q}^{\mathrm{2}} +{c}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)−\Sigma{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}} \\ $$$${R}=\frac{\mathrm{4}{A}_{{b}} }{\mathrm{3}{p}_{{b}} }=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\frac{\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\left({a}+{b}+{c}\right)}} \\ $$

Commented by ajfour last updated on 31/May/19

$${Thank}\:{you}\:{very}\:{much}\:{Sir}, \\ $$$${i}\:{think},\:{i}'{ll}\:{have}\:{to}\:{strive}\:{hard} \\ $$$${to}\:{follow}. \\ $$

Commented by mr W last updated on 31/May/19

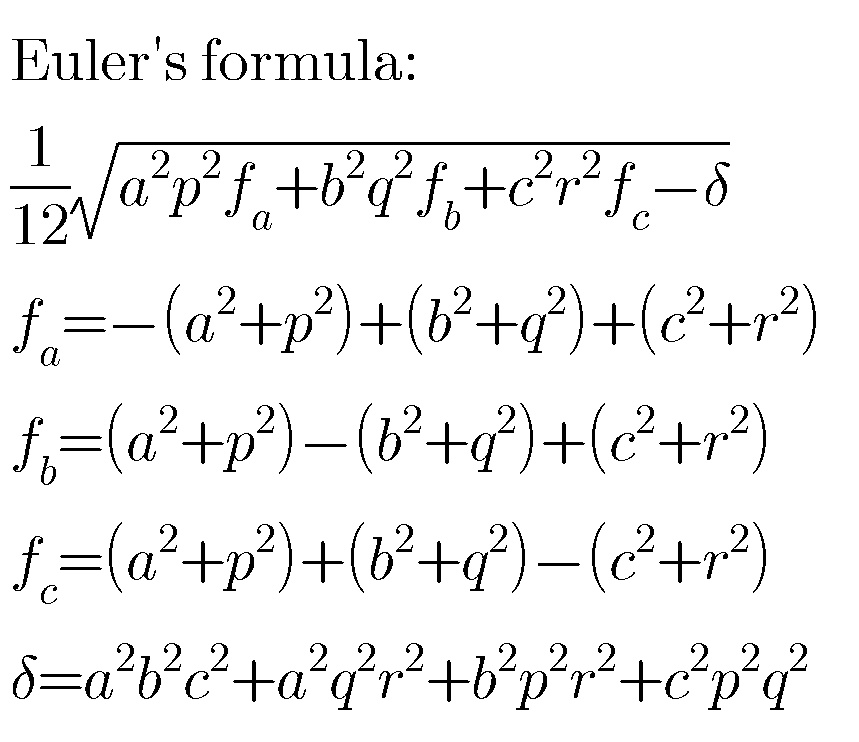
Commented by mr W last updated on 31/May/19

this is the formula for volume of a pyramid with given edge lengthes. [acc. to post from MJS sir]

$${this}\:{is}\:{the}\:{formula}\:{for}\:{volume}\:{of} \\ $$$${a}\:{pyramid}\:{with}\:{given}\:{edge}\:{lengthes}. \\ $$$$\left[{acc}.\:{to}\:{post}\:{from}\:{MJS}\:{sir}\right] \\ $$

Commented by ajfour last updated on 31/May/19

$${okay}\:{Sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply