Menu Close

Question-61241

Tinku Tara 0 Comments
Pin




Question Number 61241 by Tawa1 last updated on 30/May/19
Answered by meme last updated on 30/May/19
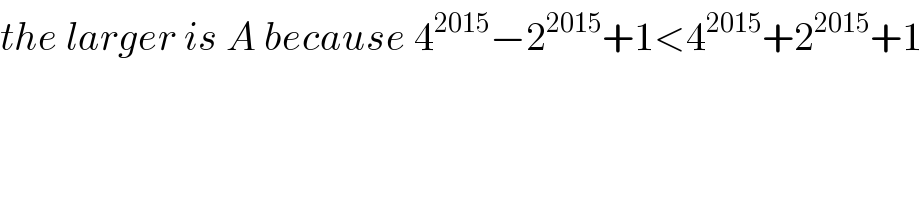
the larger is A because 4^(2015) −2^(2015) +1<4^(2015) +2^(2015) +1
$${the}\:{larger}\:{is}\:{A}\:{because}\:\mathrm{4}^{\mathrm{2015}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}<\mathrm{4}^{\mathrm{2015}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 31/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by meme last updated on 30/May/19
the larger is A because 4^(2015) −2^(2015) +1<4^(2015) +2^(2015) +1
$${the}\:{larger}\:{is}\:{A}\:{because}\:\mathrm{4}^{\mathrm{2015}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}<\mathrm{4}^{\mathrm{2015}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1} \\ $$
Answered by MJS last updated on 31/May/19
((2^x −1)/(2^(2x) −2^x +1))<?>((2^x +1)/(2^(2x) +2^x +1)) ((a−1)/(a^2 −a+1))<?>((a+1)/(a^2 +a+1)) (1/(a+(1/(a−1))))<?>(1/(a+(1/(a+1)))) now a−1<a+1 ⇒ (1/(a−1))>(1/(a+1)) ⇒ a+(1/(a−1))>a+(1/(a+1)) ⇒ ⇒ (1/(a+(1/(a−1))))<(1/(a+(1/(a+1)))) ⇒ ⇒ A<B
$$\frac{\mathrm{2}^{{x}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}{x}} −\mathrm{2}^{{x}} +\mathrm{1}}<?>\frac{\mathrm{2}^{{x}} +\mathrm{1}}{\mathrm{2}^{\mathrm{2}{x}} +\mathrm{2}^{{x}} +\mathrm{1}} \\ $$$$\frac{{a}−\mathrm{1}}{{a}^{\mathrm{2}} −{a}+\mathrm{1}}<?>\frac{{a}+\mathrm{1}}{{a}^{\mathrm{2}} +{a}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}−\mathrm{1}}}<?>\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}+\mathrm{1}}} \\ $$$$\mathrm{now} \\ $$$${a}−\mathrm{1}<{a}+\mathrm{1}\:\Rightarrow\:\frac{\mathrm{1}}{{a}−\mathrm{1}}>\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\Rightarrow\:{a}+\frac{\mathrm{1}}{{a}−\mathrm{1}}>{a}+\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}−\mathrm{1}}}<\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}+\mathrm{1}}}\:\Rightarrow \\ $$$$\Rightarrow\:{A}<{B} \\ $$
Commented by Tawa1 last updated on 31/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 31/May/19
((2^(2015) −1)/(4^(2015) −2^(2015) +1))−((2^(2015) +1)/(4^(2015) +2^(2015) +1))= =(((2^(2015) −1)(4^(2015) +2^(2015) +1)−(2^(2015) +1)(4^(2015) −2^(2015) +1))/((4^(2015) −2^(2015) +1)(4^(2015) +2^(2015) +1)))= =((−2)/(16^(2015) +4^(2015) +1))<0 ⇒ A<B
$$\frac{\mathrm{2}^{\mathrm{2015}} −\mathrm{1}}{\mathrm{4}^{\mathrm{2015}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}−\frac{\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}{\mathrm{4}^{\mathrm{2015}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}= \\ $$$$=\frac{\left(\mathrm{2}^{\mathrm{2015}} −\mathrm{1}\right)\left(\mathrm{4}^{\mathrm{2015}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1}\right)−\left(\mathrm{2}^{\mathrm{2015}} +\mathrm{1}\right)\left(\mathrm{4}^{\mathrm{2015}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}\right)}{\left(\mathrm{4}^{\mathrm{2015}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}\right)\left(\mathrm{4}^{\mathrm{2015}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1}\right)}= \\ $$$$=\frac{−\mathrm{2}}{\mathrm{16}^{\mathrm{2015}} +\mathrm{4}^{\mathrm{2015}} +\mathrm{1}}<\mathrm{0}\:\Rightarrow\:{A}<{B} \\ $$
Commented by Tawa1 last updated on 31/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 31/May/19
A=((2^(2015) −1)/((2^(2015) )^2 −2^(2015) +1))×((2^(2015) +1)/(2^(2015) +1)) =(((2^(2015) )^2 −1)/((2^(2015) )^3 +1)) B=((2^(2015) +1)/((2^(2015) )^2 +2^(2015) +1))×((2^(2015) −1)/(2^(2015) −1)) =(((2^(2015) )^2 −1)/((2^(2015) )^3 −1)) N(A)=N(B) & D(A)>D(B) ∴ A<B
$$\mathrm{A}=\frac{\mathrm{2}^{\mathrm{2015}} −\mathrm{1}}{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}×\frac{\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}{\mathrm{2}^{\mathrm{2015}} +\mathrm{1}} \\ $$$$\:\:\:=\frac{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{3}} +\mathrm{1}} \\ $$$$\mathrm{B}=\frac{\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2015}} +\mathrm{1}}×\frac{\mathrm{2}^{\mathrm{2015}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2015}} −\mathrm{1}} \\ $$$$\:\:=\frac{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{2}^{\mathrm{2015}} \right)^{\mathrm{3}} −\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{N}\left(\mathrm{A}\right)=\mathrm{N}\left(\mathrm{B}\right)\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$$\mathrm{D}\left(\mathrm{A}\right)>\mathrm{D}\left(\mathrm{B}\right)\:\:\: \\ $$$$\therefore\:\:\mathrm{A}<\mathrm{B} \\ $$
Commented by Tawa1 last updated on 31/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *