Menu Close

Question-61303

Tinku Tara 0 Comments
Pin




Question Number 61303 by mr W last updated on 31/May/19
Commented by mr W last updated on 31/May/19
A small sphere (say the moon) moves around a big sphere (say the earth) in a circular track. A point source (say the sun) is at a distance e from the center of the big sphere. Find the area of shadow of the small sphere on the surface of the big sphere in terms of α. Find the maximum shadow area. We only need to treat the case that the shadow is completely on the surface of the big sphere.
$${A}\:{small}\:{sphere}\:\left({say}\:{the}\:{moon}\right)\:{moves} \\ $$$${around}\:{a}\:{big}\:{sphere}\:\left({say}\:{the}\:{earth}\right)\:{in} \\ $$$${a}\:{circular}\:{track}.\:{A}\:{point}\:{source}\:\left({say}\right. \\ $$$$\left.{the}\:{sun}\right)\:{is}\:{at}\:{a}\:{distance}\:{e}\:{from}\:{the} \\ $$$${center}\:{of}\:{the}\:{big}\:{sphere}. \\ $$$${Find}\:{the}\:{area}\:{of}\:{shadow}\:{of}\:{the}\:{small} \\ $$$${sphere}\:{on}\:{the}\:{surface}\:{of}\:{the}\:{big} \\ $$$${sphere}\:{in}\:{terms}\:{of}\:\alpha.\:{Find}\:{the} \\ $$$${maximum}\:{shadow}\:{area}. \\ $$$${We}\:{only}\:{need}\:{to}\:{treat}\:{the}\:{case}\:{that} \\ $$$${the}\:{shadow}\:{is}\:{completely}\:{on}\:{the}\:{surface} \\ $$$${of}\:{the}\:{big}\:{sphere}. \\ $$
Commented by ajfour last updated on 02/Jun/19
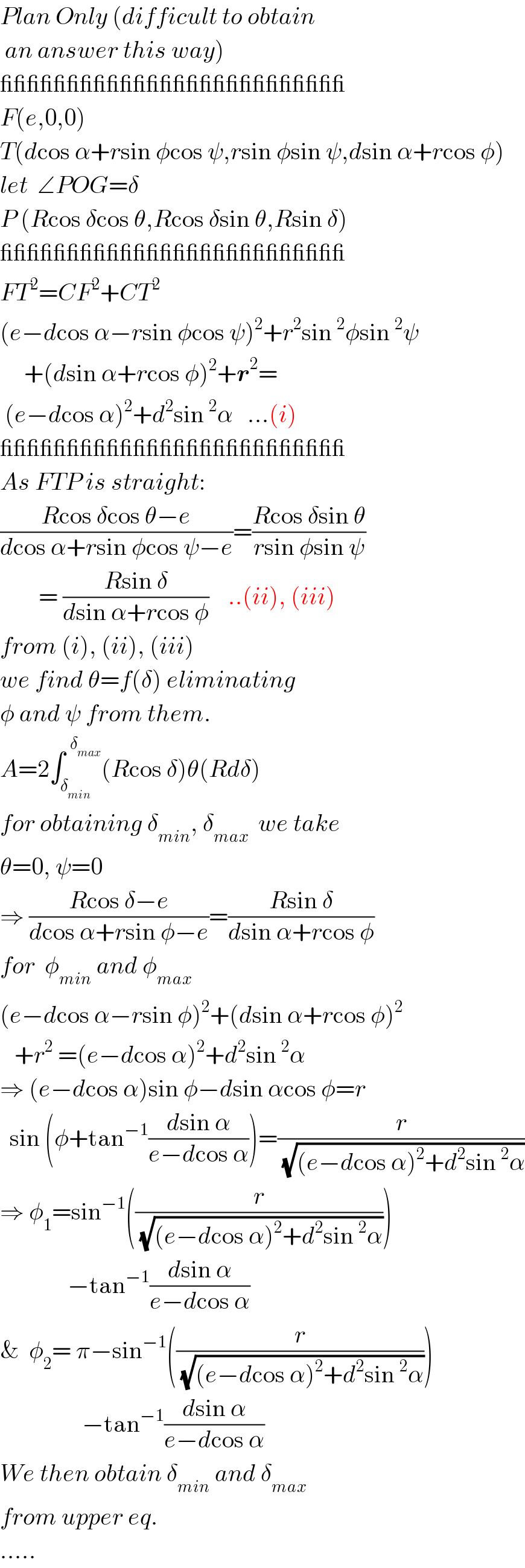
Plan Only (difficult to obtain an answer this way) __________________________ F(e,0,0) T(dcos α+rsin φcos ψ,rsin φsin ψ,dsin α+rcos φ) let ∠POG=δ P (Rcos δcos θ,Rcos δsin θ,Rsin δ) __________________________ FT^2 =CF^2 +CT^2 (e−dcos α−rsin φcos ψ)^2 +r^2 sin^2 φsin^2 ψ +(dsin α+rcos φ)^2 +r^2 = (e−dcos α)^2 +d^2 sin^2 α ...(i) __________________________ As FTP is straight: ((Rcos δcos θ−e)/(dcos α+rsin φcos ψ−e))=((Rcos δsin θ)/(rsin φsin ψ)) = ((Rsin δ)/(dsin α+rcos φ)) ..(ii), (iii) from (i), (ii), (iii) we find θ=f(δ) eliminating φ and ψ from them. A=2∫_δ_(min) ^( δ_(max) ) (Rcos δ)θ(Rdδ) for obtaining δ_(min) , δ_(max) we take θ=0, ψ=0 ⇒ ((Rcos δ−e)/(dcos α+rsin φ−e))=((Rsin δ)/(dsin α+rcos φ)) for φ_(min) and φ_(max) (e−dcos α−rsin φ)^2 +(dsin α+rcos φ)^2 +r^2 =(e−dcos α)^2 +d^2 sin^2 α ⇒ (e−dcos α)sin φ−dsin αcos φ=r sin (φ+tan^(−1) ((dsin α)/(e−dcos α)))=(r/( (√((e−dcos α)^2 +d^2 sin^2 α)))) ⇒ φ_1 =sin^(−1) ((r/( (√((e−dcos α)^2 +d^2 sin^2 α))))) −tan^(−1) ((dsin α)/(e−dcos α)) & φ_2 = π−sin^(−1) ((r/( (√((e−dcos α)^2 +d^2 sin^2 α))))) −tan^(−1) ((dsin α)/(e−dcos α)) We then obtain δ_(min) and δ_(max) from upper eq. .....
$${Plan}\:{Only}\:\left({difficult}\:{to}\:{obtain}\right. \\ $$$$\left.\:{an}\:{answer}\:{this}\:{way}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${F}\left({e},\mathrm{0},\mathrm{0}\right) \\ $$$${T}\left({d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi,{r}\mathrm{sin}\:\phi\mathrm{sin}\:\psi,{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right) \\ $$$${let}\:\:\angle{POG}=\delta \\ $$$${P}\:\left({R}\mathrm{cos}\:\delta\mathrm{cos}\:\theta,{R}\mathrm{cos}\:\delta\mathrm{sin}\:\theta,{R}\mathrm{sin}\:\delta\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${FT}^{\mathrm{2}} ={CF}^{\mathrm{2}} +{CT}^{\mathrm{2}} \\ $$$$\left({e}−{d}\mathrm{cos}\:\alpha−{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\mathrm{sin}\:^{\mathrm{2}} \psi \\ $$$$\:\:\:\:\:+\left({d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{2}} = \\ $$$$\:\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha\:\:\:…\left({i}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${As}\:{FTP}\:{is}\:{straight}: \\ $$$$\frac{{R}\mathrm{cos}\:\delta\mathrm{cos}\:\theta−{e}}{{d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi−{e}}=\frac{{R}\mathrm{cos}\:\delta\mathrm{sin}\:\theta}{{r}\mathrm{sin}\:\phi\mathrm{sin}\:\psi} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{{R}\mathrm{sin}\:\delta}{{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi}\:\:\:\:..\left({ii}\right),\:\left({iii}\right) \\ $$$${from}\:\left({i}\right),\:\left({ii}\right),\:\left({iii}\right) \\ $$$${we}\:{find}\:\theta={f}\left(\delta\right)\:{eliminating} \\ $$$$\phi\:{and}\:\psi\:{from}\:{them}. \\ $$$${A}=\mathrm{2}\int_{\delta_{{min}} } ^{\:\:\delta_{{max}} } \left({R}\mathrm{cos}\:\delta\right)\theta\left({Rd}\delta\right) \\ $$$${for}\:{obtaining}\:\delta_{{min}} ,\:\delta_{{max}} \:\:{we}\:{take} \\ $$$$\theta=\mathrm{0},\:\psi=\mathrm{0} \\ $$$$\Rightarrow\:\frac{{R}\mathrm{cos}\:\delta−{e}}{{d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi−{e}}=\frac{{R}\mathrm{sin}\:\delta}{{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi} \\ $$$${for}\:\:\phi_{{min}} \:{and}\:\phi_{{max}} \\ $$$$\left({e}−{d}\mathrm{cos}\:\alpha−{r}\mathrm{sin}\:\phi\right)^{\mathrm{2}} +\left({d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:+{r}^{\mathrm{2}} \:=\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\Rightarrow\:\left({e}−{d}\mathrm{cos}\:\alpha\right)\mathrm{sin}\:\phi−{d}\mathrm{sin}\:\alpha\mathrm{cos}\:\phi={r}\: \\ $$$$\:\:\mathrm{sin}\:\left(\phi+\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha}\right)=\frac{{r}}{\:\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}} \\ $$$$\Rightarrow\:\phi_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}}{\:\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha} \\ $$$$\&\:\:\phi_{\mathrm{2}} =\:\pi−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}}{\:\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha} \\ $$$${We}\:{then}\:{obtain}\:\delta_{{min}} \:{and}\:\delta_{{max}} \\ $$$${from}\:{upper}\:{eq}. \\ $$$$….. \\ $$
Commented by mr W last updated on 01/Jun/19
thanks for trying sir! i have not got a solution. but your method would be that what i had also used. but on the other side i think there should be an other maybe easier way. i′ll try it later.
$${thanks}\:{for}\:{trying}\:{sir}!\:{i}\:{have}\:{not}\:{got} \\ $$$${a}\:{solution}.\:{but}\:{your}\:{method}\:{would}\:{be} \\ $$$${that}\:{what}\:{i}\:{had}\:{also}\:{used}.\:{but}\:{on}\:{the} \\ $$$${other}\:{side}\:{i}\:{think}\:{there}\:{should}\:{be}\:{an} \\ $$$${other}\:{maybe}\:{easier}\:{way}.\:{i}'{ll}\:{try}\:{it} \\ $$$${later}. \\ $$
Answered by ajfour last updated on 02/Jun/19
Answered by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
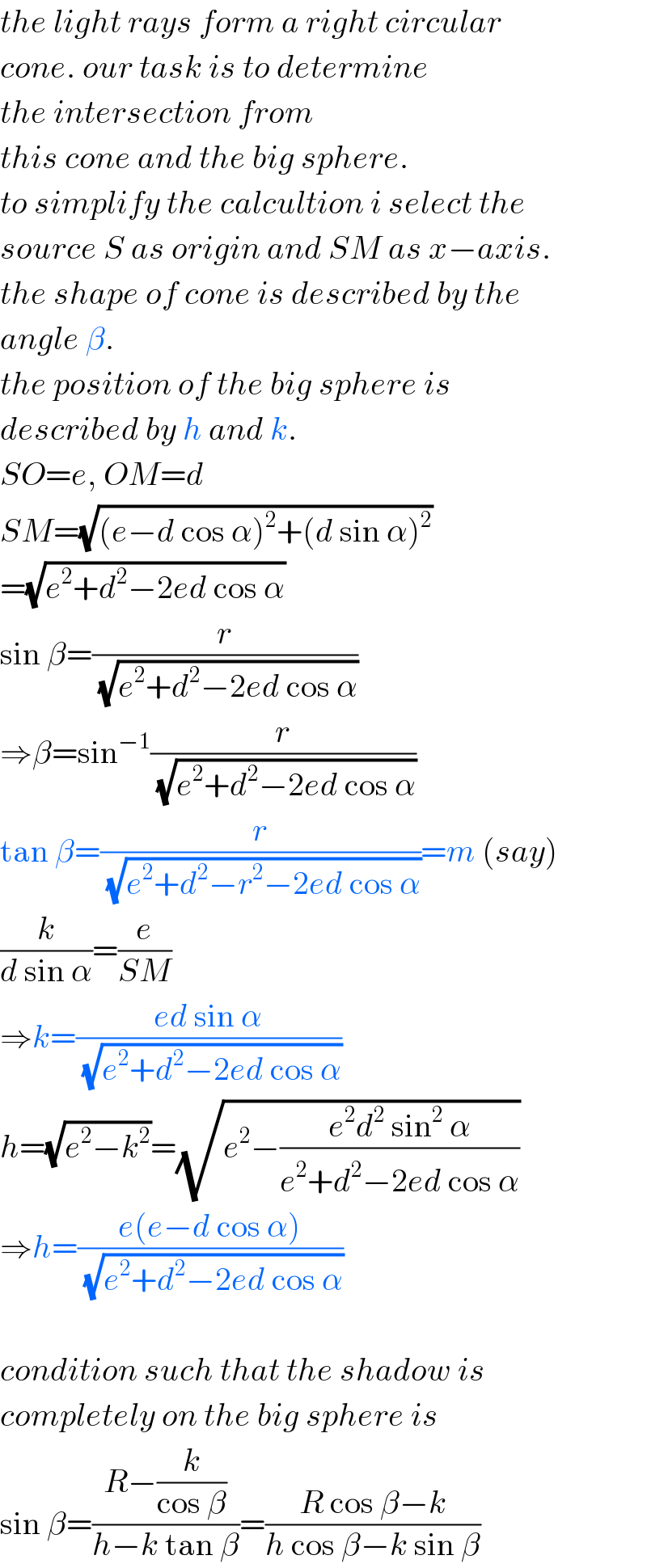
the light rays form a right circular cone. our task is to determine the intersection from this cone and the big sphere. to simplify the calcultion i select the source S as origin and SM as x−axis. the shape of cone is described by the angle β. the position of the big sphere is described by h and k. SO=e, OM=d SM=(√((e−d cos α)^2 +(d sin α)^2 )) =(√(e^2 +d^2 −2ed cos α)) sin β=(r/( (√(e^2 +d^2 −2ed cos α)))) ⇒β=sin^(−1) (r/( (√(e^2 +d^2 −2ed cos α)))) tan β=(r/( (√(e^2 +d^2 −r^2 −2ed cos α))))=m (say) (k/(d sin α))=(e/(SM)) ⇒k=((ed sin α)/( (√(e^2 +d^2 −2ed cos α)))) h=(√(e^2 −k^2 ))=(√(e^2 −((e^2 d^2 sin^2 α)/(e^2 +d^2 −2ed cos α)))) ⇒h=((e(e−d cos α))/( (√(e^2 +d^2 −2ed cos α)))) condition such that the shadow is completely on the big sphere is sin β=((R−(k/(cos β)))/(h−k tan β))=((R cos β−k)/(h cos β−k sin β))
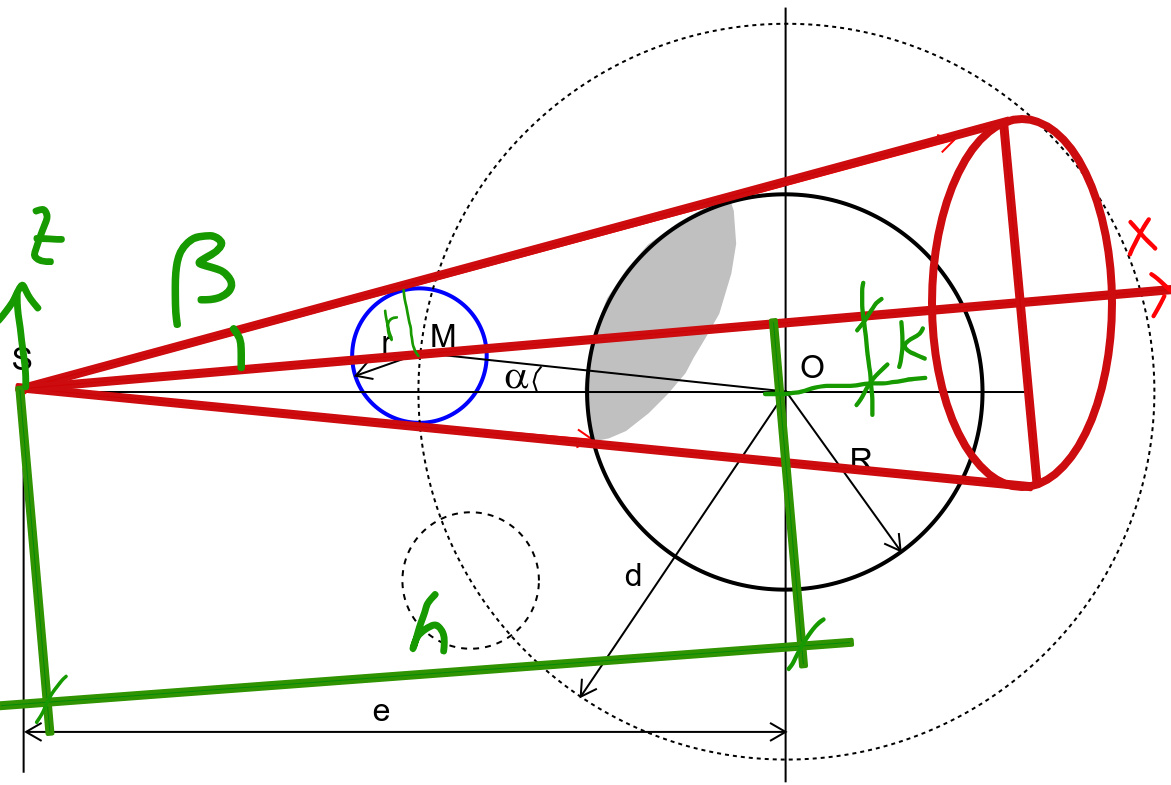
$${the}\:{light}\:{rays}\:{form}\:{a}\:{right}\:{circular} \\ $$$${cone}.\:{our}\:{task}\:{is}\:{to}\:{determine} \\ $$$${the}\:{intersection}\:{from} \\ $$$${this}\:{cone}\:{and}\:{the}\:{big}\:{sphere}. \\ $$$${to}\:{simplify}\:{the}\:{calcultion}\:{i}\:{select}\:{the} \\ $$$${source}\:{S}\:{as}\:{origin}\:{and}\:{SM}\:{as}\:{x}−{axis}. \\ $$$${the}\:{shape}\:{of}\:{cone}\:{is}\:{described}\:{by}\:{the} \\ $$$${angle}\:\beta. \\ $$$${the}\:{position}\:{of}\:{the}\:{big}\:{sphere}\:{is} \\ $$$${described}\:{by}\:{h}\:{and}\:{k}. \\ $$$${SO}={e},\:{OM}={d} \\ $$$${SM}=\sqrt{\left({e}−{d}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left({d}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} } \\ $$$$=\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha} \\ $$$$\mathrm{sin}\:\beta=\frac{{r}}{\:\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{\:\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\mathrm{tan}\:\beta=\frac{{r}}{\:\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −{r}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}}={m}\:\left({say}\right) \\ $$$$\frac{{k}}{{d}\:\mathrm{sin}\:\alpha}=\frac{{e}}{{SM}} \\ $$$$\Rightarrow{k}=\frac{{ed}\:\mathrm{sin}\:\alpha}{\:\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$${h}=\sqrt{{e}^{\mathrm{2}} −{k}^{\mathrm{2}} }=\sqrt{{e}^{\mathrm{2}} −\frac{{e}^{\mathrm{2}} {d}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha}{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\Rightarrow{h}=\frac{{e}\left({e}−{d}\:\mathrm{cos}\:\alpha\right)}{\:\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$ \\ $$$${condition}\:{such}\:{that}\:{the}\:{shadow}\:{is} \\ $$$${completely}\:{on}\:{the}\:{big}\:{sphere}\:{is} \\ $$$$\mathrm{sin}\:\beta=\frac{{R}−\frac{{k}}{\mathrm{cos}\:\beta}}{{h}−{k}\:\mathrm{tan}\:\beta}=\frac{{R}\:\mathrm{cos}\:\beta−{k}}{{h}\:\mathrm{cos}\:\beta−{k}\:\mathrm{sin}\:\beta} \\ $$
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 03/Jun/19
eqn. of cone: x=((√(y^2 +z^2 ))/(tan β))=((√(y^2 +z^2 ))/m) or y^2 =m^2 x^2 −z^2 eqn. of sphere: (x−h)^2 +y^2 +(z+k)^2 =R^2 intersection of cone and sphere: (x−h)^2 +m^2 x^2 −z^2 +(z+k)^2 =R^2 ⇒(1+m^2 )x^2 −2hx+2kz+(h^2 +k^2 −R^2 )=0 ...(i) (this is a parabola in xz−plane) at θ: let ρ=R−Δh x=h−ρ cos θ z=−k+ρ sin θ put this into (i): (1+m^2 )[h−ρ cos θ]^2 −2h[h−ρ cos θ]+2k[−k+ρ sin θ]+(h^2 +k^2 −R^2 )=0 (1+m^2 )cos^2 θ ρ^2 −2(m^2 h cos θ−k sin θ)ρ+(m^2 h^2 −k^2 −R^2 )=0 ⇒ρ=(((m^2 h cos θ−k sin θ)+(√(m^4 h^2 cos^2 θ+k^2 sin^2 θ−2m^2 hk sin θ cos θ−(1+m^2 )cos^2 θ(m^2 h^2 −k^2 −R^2 ))))/((1+m^2 )cos^2 θ)) (two intersections, we take + for the left one) ⇒ρ=R cos ϕ=(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )cos^2 θ)) ⇒ϕ=cos^(−1) {(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )R cos^2 θ))} for ρ=(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )cos^2 θ))=R we get θ_1 and θ_2 . Area of shadow=A A=∫_θ_1 ^θ_2 2RϕRdθ ⇒A=2R^2 ∫_θ_1 ^θ_2 cos^(−1) {(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )R cos^2 θ))}dθ with μ=(k/R),λ=(h/R) ⇒A=2R^2 ∫_θ_1 ^θ_2 cos^(−1) {((m^2 λ cos θ−μ sin θ+(√(μ^2 +[1+m^2 (1+μ^2 −λ^2 )]cos^2 θ−m^2 λμ sin 2θ)))/((1+m^2 )cos^2 θ))}dθ
$${eqn}.\:{of}\:{cone}: \\ $$$${x}=\frac{\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{\mathrm{tan}\:\beta}=\frac{\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{{m}} \\ $$$${or}\:{y}^{\mathrm{2}} ={m}^{\mathrm{2}} {x}^{\mathrm{2}} −{z}^{\mathrm{2}} \\ $$$$ \\ $$$${eqn}.\:{of}\:{sphere}: \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({z}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$ \\ $$$${intersection}\:{of}\:{cone}\:{and}\:{sphere}: \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +{m}^{\mathrm{2}} {x}^{\mathrm{2}} −{z}^{\mathrm{2}} +\left({z}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\mathrm{2}{hx}+\mathrm{2}{kz}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\left({this}\:{is}\:{a}\:{parabola}\:{in}\:{xz}−{plane}\right) \\ $$$$ \\ $$$${at}\:\theta: \\ $$$${let}\:\rho={R}−\Delta{h} \\ $$$${x}={h}−\rho\:\mathrm{cos}\:\theta \\ $$$${z}=−{k}+\rho\:\mathrm{sin}\:\theta \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left[{h}−\rho\:\mathrm{cos}\:\theta\right]^{\mathrm{2}} −\mathrm{2}{h}\left[{h}−\rho\:\mathrm{cos}\:\theta\right]+\mathrm{2}{k}\left[−{k}+\rho\:\mathrm{sin}\:\theta\right]+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta\:\rho^{\mathrm{2}} −\mathrm{2}\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)\rho+\left({m}^{\mathrm{2}} {h}^{\mathrm{2}} −{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\rho=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{m}^{\mathrm{4}} {h}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+{k}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{2}{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta\left({m}^{\mathrm{2}} {h}^{\mathrm{2}} −{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\left({two}\:{intersections},\:{we}\:{take}\:+\:{for}\:{the}\:{left}\:{one}\right) \\ $$$$\Rightarrow\rho={R}\:\mathrm{cos}\:\varphi=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\varphi=\mathrm{cos}^{−\mathrm{1}} \left\{\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right\} \\ $$$${for}\:\rho=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}={R} \\ $$$${we}\:{get}\:\theta_{\mathrm{1}} \:{and}\:\theta_{\mathrm{2}} . \\ $$$$ \\ $$$${Area}\:{of}\:{shadow}={A} \\ $$$${A}=\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{2}{R}\varphi{Rd}\theta \\ $$$$\Rightarrow{A}=\mathrm{2}{R}^{\mathrm{2}} \int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{cos}^{−\mathrm{1}} \left\{\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right\}{d}\theta \\ $$$${with}\:\mu=\frac{{k}}{{R}},\lambda=\frac{{h}}{{R}} \\ $$$$\Rightarrow{A}=\mathrm{2}{R}^{\mathrm{2}} \int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{cos}^{−\mathrm{1}} \left\{\frac{{m}^{\mathrm{2}} \lambda\:\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta+\sqrt{\mu^{\mathrm{2}} +\left[\mathrm{1}+{m}^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} −\lambda^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} \lambda\mu\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}\right\}{d}\theta \\ $$
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by ajfour last updated on 02/Jun/19
Great Sir, but you′ll have to guide me to the idea used, i dont think i′ll follow it otherwise..
$${Great}\:{Sir},\:{but}\:{you}'{ll}\:{have}\:{to} \\ $$$${guide}\:{me}\:{to}\:{the}\:{idea}\:{used},\:{i}\:{dont} \\ $$$${think}\:{i}'{ll}\:{follow}\:{it}\:{otherwise}.. \\ $$
Commented by mr W last updated on 02/Jun/19
the boundary of the shadow on the surface of big sphere is the intersection (a curve in the space) from the cone and the big sphere. the shape of the cone is given by the size of the small sphere. with the coordinate system i select the eqn. of the cone and the big sphere can be described in simple form. the eqn. of the intersection line in the xz−plane can be obtained quite easily, and it′s a parabola. with this eqn. we can determine the parameters of the shadow area on the sphere surface. the parameters are: θ and ρ (i.e. ϕ).
$${the}\:{boundary}\:{of}\:{the}\:{shadow}\:{on}\:{the} \\ $$$${surface}\:{of}\:{big}\:{sphere}\:{is}\:{the}\:{intersection} \\ $$$$\left({a}\:{curve}\:{in}\:{the}\:{space}\right)\:{from}\:{the}\:{cone} \\ $$$${and}\:{the}\:{big}\:{sphere}.\:{the}\:{shape}\:{of}\:{the} \\ $$$${cone}\:{is}\:{given}\:{by}\:{the}\:{size}\:{of}\:{the}\:{small} \\ $$$${sphere}.\:{with}\:{the}\:{coordinate}\:{system} \\ $$$${i}\:{select}\:{the}\:{eqn}.\:{of}\:{the}\:{cone}\:{and}\:{the} \\ $$$${big}\:{sphere}\:{can}\:{be}\:{described}\:{in}\:{simple} \\ $$$${form}.\:{the}\:{eqn}.\:{of}\:{the}\:{intersection} \\ $$$${line}\:{in}\:{the}\:{xz}−{plane}\:{can}\:{be}\:{obtained} \\ $$$${quite}\:{easily},\:{and}\:{it}'{s}\:{a}\:{parabola}.\:{with} \\ $$$${this}\:{eqn}.\:{we}\:{can}\:{determine}\:{the} \\ $$$${parameters}\:{of}\:{the}\:{shadow}\:{area}\:{on} \\ $$$${the}\:{sphere}\:{surface}.\:{the}\:{parameters} \\ $$$${are}:\:\theta\:{and}\:\rho\:\left({i}.{e}.\:\varphi\right). \\ $$
Commented by ajfour last updated on 06/Jun/19
I am very thankful but i lack the required patience (these days) Sir, i have saved your solution, and shall analyse it soon.
$${I}\:{am}\:{very}\:{thankful}\:{but}\:{i}\:{lack} \\ $$$${the}\:{required}\:{patience}\:\left({these}\:{days}\right) \\ $$$${Sir},\:{i}\:{have}\:{saved}\:{your}\:{solution}, \\ $$$${and}\:{shall}\:{analyse}\:{it}\:{soon}. \\ $$
Commented by mr W last updated on 06/Jun/19
thank you sir! i wasn′t able to provide a better and complete solution. but i′ll try to continue to think about the question. i hope one day you may give a perfect solution sir.
$${thank}\:{you}\:{sir}! \\ $$$${i}\:{wasn}'{t}\:{able}\:{to}\:{provide}\:{a}\:{better}\:{and} \\ $$$${complete}\:{solution}.\:\:{but}\:{i}'{ll}\:{try}\:{to} \\ $$$${continue}\:{to}\:{think}\:{about}\:{the}\:{question}. \\ $$$${i}\:{hope}\:{one}\:{day}\:{you}\:{may}\:{give}\:{a}\:{perfect} \\ $$$${solution}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *