Question Number 61335 by necx1 last updated on 01/Jun/19
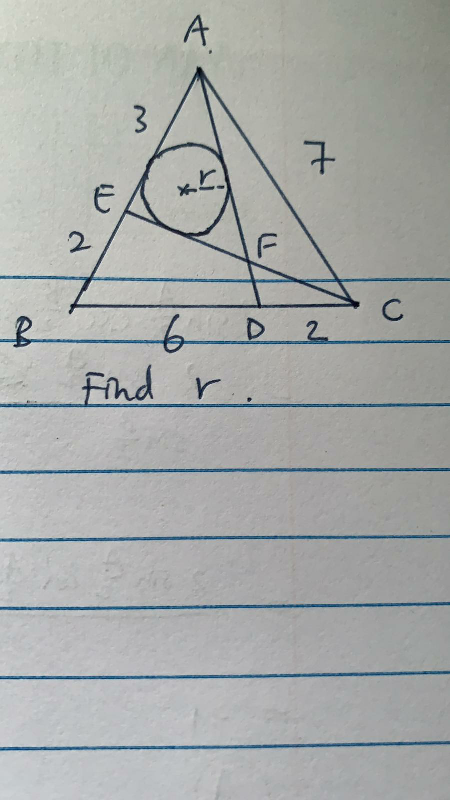
Answered by mr W last updated on 02/Jun/19
![cos ∠A=((5^2 +7^2 −8^2 )/(2×5×7))=(1/7) ⇒sin ∠A=((4(√3))/7) cos ∠B=((5^2 +8^2 −7^2 )/(2×5×8))=(1/2) ⇒∠B=60° ⇒sin ∠B=((√3)/2) cos ∠C=((8^2 +7^2 −5^2 )/(2×8×7))=((11)/(14)) ⇒sin ∠C=((5(√3))/(14)) EC=(√(2^2 +8^2 −2×2×8×(1/2)))=2(√(13)) AD=(√(2^2 +7^2 −2×2×7×((11)/(14))))=(√(31)) ((sin ∠BAD)/6)=((sin ∠B)/( (√(31)))) ⇒sin ∠BAD=((6×(√3))/(2×(√(31))))=((3(√(93)))/(31)) ⇒tan ((∠BAD)/2)=((3(√(93)))/(31[1+(√(1−(((3(√(93)))/(31)))^2 ))]))=((3(√3))/(2+(√(31)))) ((sin ∠AEC)/7)=((sin ∠A)/(2(√(13)))) ⇒sin ∠AEC=((7×4(√3))/(7×2(√(13))))=((2(√(39)))/(13)) ⇒tan ((∠AEC)/2)=((2(√(39)))/(13[1+(√(1−(((2(√(39)))/(13)))^2 ))]))=((2(√3))/(1+(√(13)))) (r/(tan ((∠BAD)/2)))+(r/(tan ((∠AEC)/2)))=3 ⇒r=(3/(((2+(√(31)))/(3(√3)))+((1+(√(13)))/(2(√3)))))=((18(√3))/(7+3(√(13))+2(√(31))))=1.077](https://www.tinkutara.com/question/Q61341.png)
$$\mathrm{cos}\:\angle{A}=\frac{\mathrm{5}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{A}=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{7}} \\ $$$$\mathrm{cos}\:\angle{B}=\frac{\mathrm{5}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\angle{B}=\mathrm{60}° \\ $$$$\Rightarrow\mathrm{sin}\:\angle{B}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\angle{C}=\frac{\mathrm{8}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×\mathrm{7}}=\frac{\mathrm{11}}{\mathrm{14}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{C}=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$$${EC}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{2}×\mathrm{2}×\mathrm{8}×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{13}} \\ $$$${AD}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{2}×\mathrm{2}×\mathrm{7}×\frac{\mathrm{11}}{\mathrm{14}}}=\sqrt{\mathrm{31}} \\ $$$$\frac{\mathrm{sin}\:\angle{BAD}}{\mathrm{6}}=\frac{\mathrm{sin}\:\angle{B}}{\:\sqrt{\mathrm{31}}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{BAD}=\frac{\mathrm{6}×\sqrt{\mathrm{3}}}{\mathrm{2}×\sqrt{\mathrm{31}}}=\frac{\mathrm{3}\sqrt{\mathrm{93}}}{\mathrm{31}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\angle{BAD}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{93}}}{\mathrm{31}\left[\mathrm{1}+\sqrt{\mathrm{1}−\left(\frac{\mathrm{3}\sqrt{\mathrm{93}}}{\mathrm{31}}\right)^{\mathrm{2}} }\right]}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{31}}} \\ $$$$\frac{\mathrm{sin}\:\angle{AEC}}{\mathrm{7}}=\frac{\mathrm{sin}\:\angle{A}}{\mathrm{2}\sqrt{\mathrm{13}}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{AEC}=\frac{\mathrm{7}×\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{7}×\mathrm{2}\sqrt{\mathrm{13}}}=\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{13}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\angle{AEC}}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{13}\left[\mathrm{1}+\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}\sqrt{\mathrm{39}}}{\mathrm{13}}\right)^{\mathrm{2}} }\right]}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{13}}} \\ $$$$\frac{{r}}{\mathrm{tan}\:\frac{\angle{BAD}}{\mathrm{2}}}+\frac{{r}}{\mathrm{tan}\:\frac{\angle{AEC}}{\mathrm{2}}}=\mathrm{3} \\ $$$$\Rightarrow{r}=\frac{\mathrm{3}}{\frac{\mathrm{2}+\sqrt{\mathrm{31}}}{\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}\sqrt{\mathrm{3}}}}=\frac{\mathrm{18}\sqrt{\mathrm{3}}}{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{13}}+\mathrm{2}\sqrt{\mathrm{31}}}=\mathrm{1}.\mathrm{077} \\ $$
Commented by tanmay last updated on 01/Jun/19

$${excellent}\:{sir}… \\ $$
Commented by Tawa1 last updated on 02/Jun/19
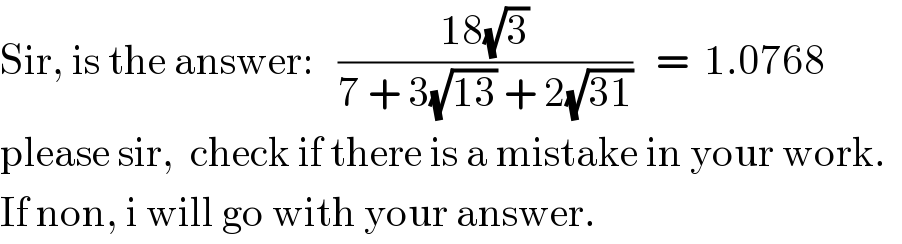
$$\mathrm{Sir},\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer}:\:\:\:\frac{\mathrm{18}\sqrt{\mathrm{3}}}{\mathrm{7}\:+\:\mathrm{3}\sqrt{\mathrm{13}}\:+\:\mathrm{2}\sqrt{\mathrm{31}}}\:\:\:=\:\:\mathrm{1}.\mathrm{0768} \\ $$$$\mathrm{please}\:\mathrm{sir},\:\:\mathrm{check}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{your}\:\mathrm{work}.\:\: \\ $$$$\mathrm{If}\:\mathrm{non},\:\mathrm{i}\:\mathrm{will}\:\mathrm{go}\:\mathrm{with}\:\mathrm{your}\:\mathrm{answer}. \\ $$
Commented by mr W last updated on 02/Jun/19

$${you}\:{are}\:{right},\:{thanks}! \\ $$$${i}\:{had}\:{a}\:{mistake}\:{due}\:{to}\:{typo}. \\ $$
Commented by Tawa1 last updated on 02/Jun/19

$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{checking}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by necx1 last updated on 04/Jun/19

$${excellent}\:{sir} \\ $$
