Question-61424

Question Number 61424 by Tawa1 last updated on 02/Jun/19

Answered by mr W last updated on 02/Jun/19

Commented by mr W last updated on 02/Jun/19

cos α=sin β=(b/(2a)) ⇒α=cos^(−1) (b/(2a)) ⇒β=sin^(−1) (b/(2a)) A_(shade) =πb^2 −(b^2 /2)(2α−sin 2α)−(a^2 /2)(4β−sin 4β) A_(shade) =πb^2 −(b^2 /2)[2 cos^(−1) (b/(2a))−sin (2 cos^(−1) (b/(2a)))]−(a^2 /2)[4 sin^(−1) (b/(2a))−sin (4 sin^(−1) (b/(2a)))]

$$\mathrm{cos}\:\alpha=\mathrm{sin}\:\beta=\frac{{b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}} \\ $$$${A}_{{shade}} =\pi{b}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right)−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{4}\beta−\mathrm{sin}\:\mathrm{4}\beta\right) \\ $$$${A}_{{shade}} =\pi{b}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}}−\mathrm{sin}\:\left(\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}}\right)\right]−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{4}\:\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}}−\mathrm{sin}\:\left(\mathrm{4}\:\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{a}}\right)\right] \\ $$

Commented by Tawa1 last updated on 02/Jun/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by alphaprime last updated on 02/Jun/19

Amazing

Commented by mr W last updated on 02/Jun/19

Commented by ajfour last updated on 02/Jun/19

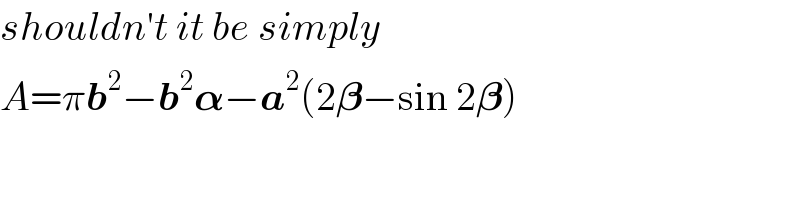
shouldn′t it be simply A=πb^2 −b^2 𝛂−a^2 (2𝛃−sin 2𝛃)

$${shouldn}'{t}\:{it}\:{be}\:{simply} \\ $$$${A}=\pi\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{\alpha}−\boldsymbol{{a}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\beta}−\mathrm{sin}\:\mathrm{2}\boldsymbol{\beta}\right)\: \\ $$

Commented by mr W last updated on 02/Jun/19

$${it}\:{can}\:{be}\:{simplified}\:{further}. \\ $$

Commented by mr W last updated on 02/Jun/19

Commented by mr W last updated on 02/Jun/19

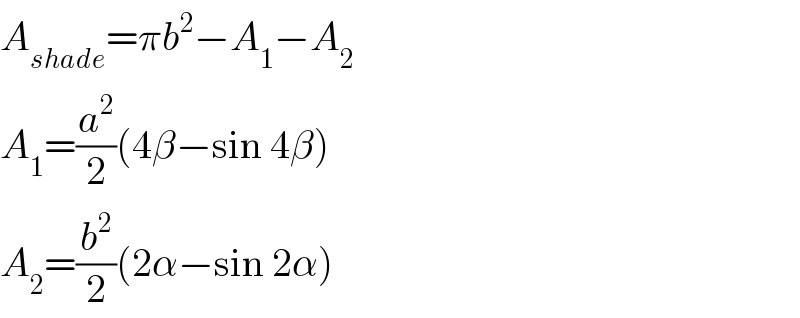
A_(shade) =πb^2 −A_1 −A_2 A_1 =(a^2 /2)(4β−sin 4β) A_2 =(b^2 /2)(2α−sin 2α)

$${A}_{{shade}} =\pi{b}^{\mathrm{2}} −{A}_{\mathrm{1}} −{A}_{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{4}\beta−\mathrm{sin}\:\mathrm{4}\beta\right) \\ $$$${A}_{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$

Commented by mr W last updated on 02/Jun/19

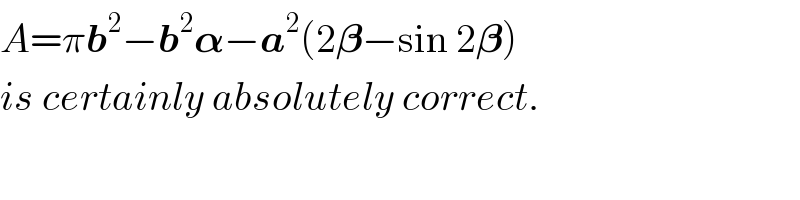
A=πb^2 −b^2 𝛂−a^2 (2𝛃−sin 2𝛃) is certainly absolutely correct.

$${A}=\pi\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{\alpha}−\boldsymbol{{a}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\beta}−\mathrm{sin}\:\mathrm{2}\boldsymbol{\beta}\right)\: \\ $$$${is}\:{certainly}\:{absolutely}\:{correct}. \\ $$

Commented by ajfour last updated on 02/Jun/19