Question Number 61495 by bhanukumarb2@gmail.com last updated on 03/Jun/19

Commented by bhanukumarb2@gmail.com last updated on 03/Jun/19

$${prove}\:{second}\:{in}\:{which}\:{book}\:{i}\:{can}\:{get}\: \\ $$$${these}\:{type}\:{approximation} \\ $$
Commented by bhanukumarb2@gmail.com last updated on 03/Jun/19

$${prove}\:{by}\:{mvt}\: \\ $$
Commented by tanmay last updated on 03/Jun/19

$${we}\:{have}\:{to}\:{prove}\:\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{cosx}\right)>\mathrm{1} \\ $$$${from}\:{graph}\:\:{it}\:{is}\:{clear}… \\ $$$$ \\ $$
Commented by tanmay last updated on 03/Jun/19
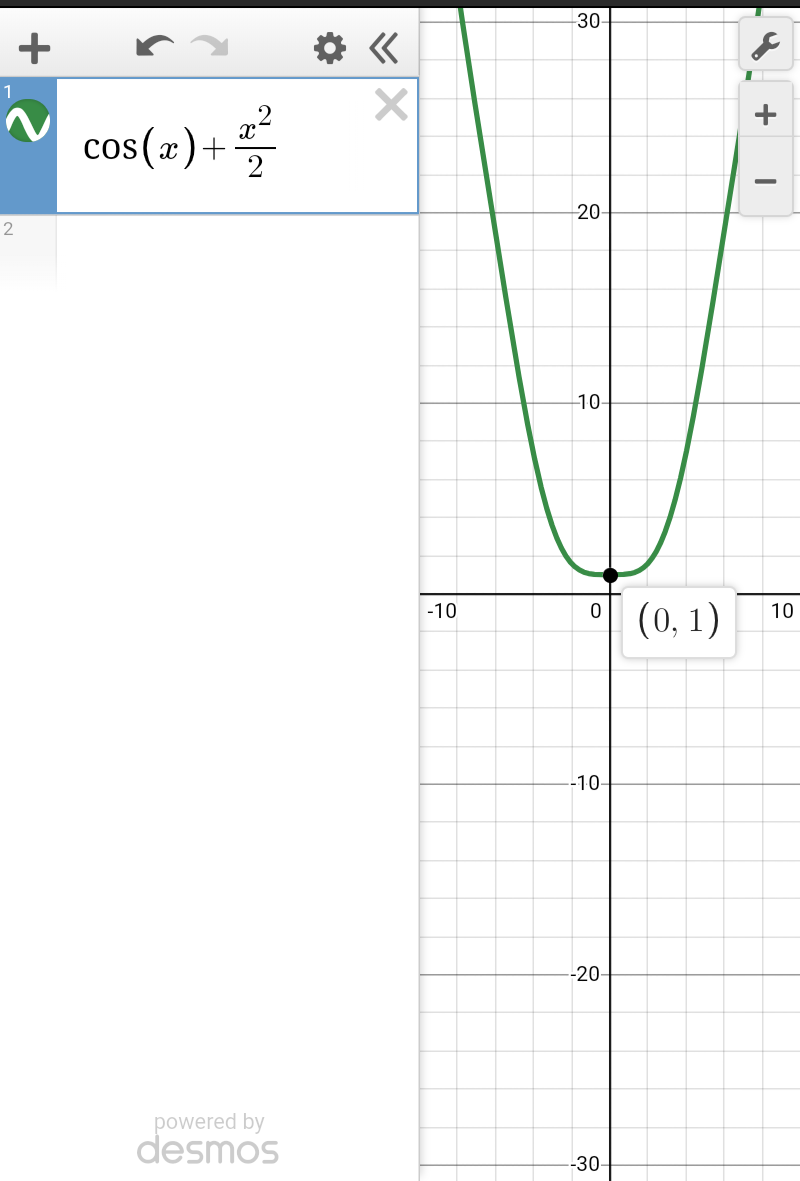
Commented by tanmay last updated on 03/Jun/19

Commented by tanmay last updated on 03/Jun/19

Commented by tanmay last updated on 03/Jun/19

Answered by MJS last updated on 03/Jun/19

$${f}\left({x}\right)=\mathrm{cos}\:{x}\:\mathrm{has}\:\mathrm{a}\:\mathrm{local}\:\mathrm{maximum}\:\mathrm{at}\:{x}=\mathrm{0} \\ $$$${g}\left({x}\right)=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{has}\:\mathrm{an}\:\mathrm{absolute}\:\mathrm{maximum}\:\mathrm{ar}\:{x}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)={g}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{curvature}\:\mathrm{of}\:\mathrm{a}\:\mathrm{given}\:\mathrm{function}\:{u}\:\mathrm{is} \\ $$$$\frac{{u}''}{\left(\mathrm{1}+{u}'^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\mathrm{the}\:\mathrm{curvature}\:\mathrm{of}\:{f}\left({x}\right)\:\mathrm{is} \\ $$$${c}_{{f}} \left({x}\right)=−\frac{\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\mathrm{the}\:\mathrm{curvature}\:\mathrm{of}\:{g}\left({x}\right)\:\mathrm{is} \\ $$$${c}_{{g}} \left({x}\right)=−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${c}_{{f}} \left(\mathrm{0}\right)={c}_{{g}} \left(\mathrm{0}\right)=−\mathrm{1} \\ $$$${c}_{{f}} '\left(\mathrm{0}\right)={c}_{{g}} '\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${c}_{{f}} ''\left(\mathrm{0}\right)=\mathrm{4} \\ $$$${c}_{{g}} ''\left(\mathrm{0}\right)=\mathrm{3} \\ $$$$\Rightarrow\:{c}_{{f}} '\:\mathrm{is}\:\mathrm{changing}\:\mathrm{faster}\:\mathrm{than}\:{c}_{{g}} ' \\ $$$$\Rightarrow\:{c}_{{f}} \:\mathrm{is}\:\mathrm{bent}\:\mathrm{harder}\:\mathrm{towards}\:{y}=\mathrm{0}\:\mathrm{than}\:{c}_{{g}} \\ $$$$\Rightarrow\:{f}\:\mathrm{is}\:\mathrm{bent}\:\mathrm{less}\:\mathrm{than}\:{g} \\ $$$$\Rightarrow\:\mathrm{because}\:\mathrm{we}\:\mathrm{know}\:\mathrm{both}\:\mathrm{share}\:\mathrm{the} \\ $$$$\:\:\:\:\:\:\:\mathrm{maximum}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{1}}\end{pmatrix}\:\Rightarrow\:{f}\geqslant{g} \\ $$
