Question Number 61554 by ajfour last updated on 04/Jun/19
Commented by ajfour last updated on 04/Jun/19

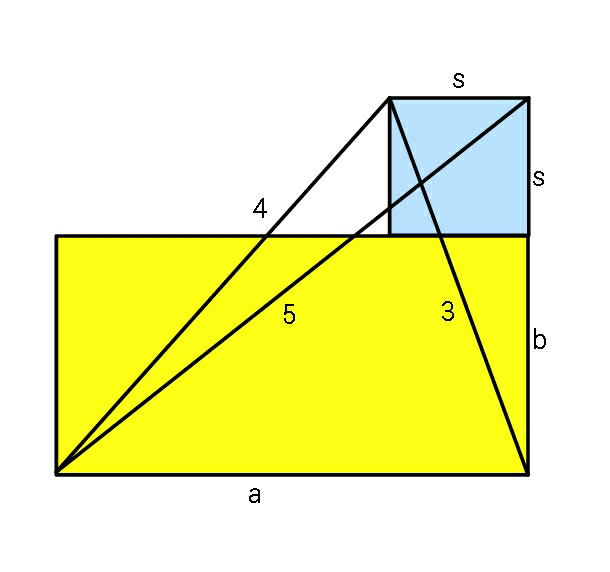
$${Find}\:{a},{b},\:{and}\:{s}. \\ $$
Answered by MJS last updated on 04/Jun/19

$${a}^{\mathrm{2}} +\left({b}+{s}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\left({a}−{s}\right)^{\mathrm{2}} +\left({b}+{s}\right)^{\mathrm{2}} =\mathrm{16} \\ $$$${s}^{\mathrm{2}} +\left({b}+{s}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{solving}\:\mathrm{these}\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{25}+\mathrm{2}\sqrt{\mathrm{193}}}\approx\mathrm{4}.\mathrm{19463} \\ $$$${b}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\sqrt{\mathrm{50}−\mathrm{2}\sqrt{\mathrm{193}}}−\sqrt{−\mathrm{23}+\mathrm{2}\sqrt{\mathrm{193}}}\right)\approx\mathrm{1}.\mathrm{45830} \\ $$$${s}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{−\mathrm{23}+\mathrm{2}\sqrt{\mathrm{193}}}\approx\mathrm{1}.\mathrm{26292} \\ $$
Commented by ajfour last updated on 04/Jun/19

$${Thanks}\:{Sir},\:{i}\:{shall}\:{check}. \\ $$
