Question Number 61675 by peter frank last updated on 06/Jun/19
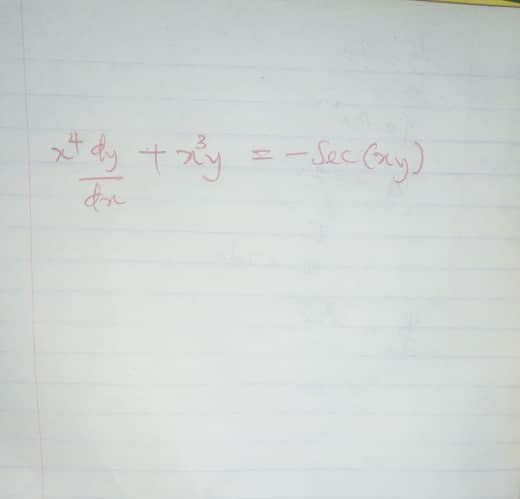
Commented by peter frank last updated on 06/Jun/19
$${find}\:\:{solution}\:{of}\:{D}.{E} \\ $$
Answered by ajfour last updated on 06/Jun/19
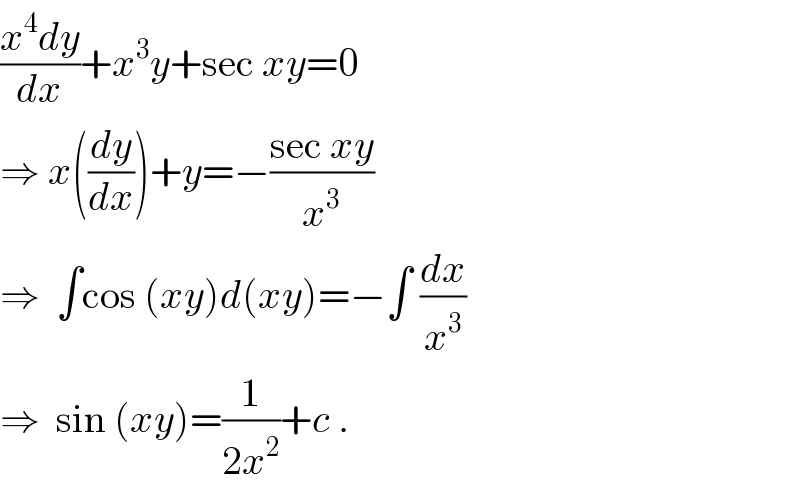
$$\frac{{x}^{\mathrm{4}} {dy}}{{dx}}+{x}^{\mathrm{3}} {y}+\mathrm{sec}\:{xy}=\mathrm{0} \\ $$$$\Rightarrow\:{x}\left(\frac{{dy}}{{dx}}\right)+{y}=−\frac{\mathrm{sec}\:{xy}}{{x}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\:\int\mathrm{cos}\:\left({xy}\right){d}\left({xy}\right)=−\int\:\frac{{dx}}{{x}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\left({xy}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+{c}\:. \\ $$
Commented by peter frank last updated on 06/Jun/19

$${thank}\:{you} \\ $$
