Menu Close

Question-62023

Tinku Tara 0 Comments
Pin




Question Number 62023 by aliesam last updated on 14/Jun/19
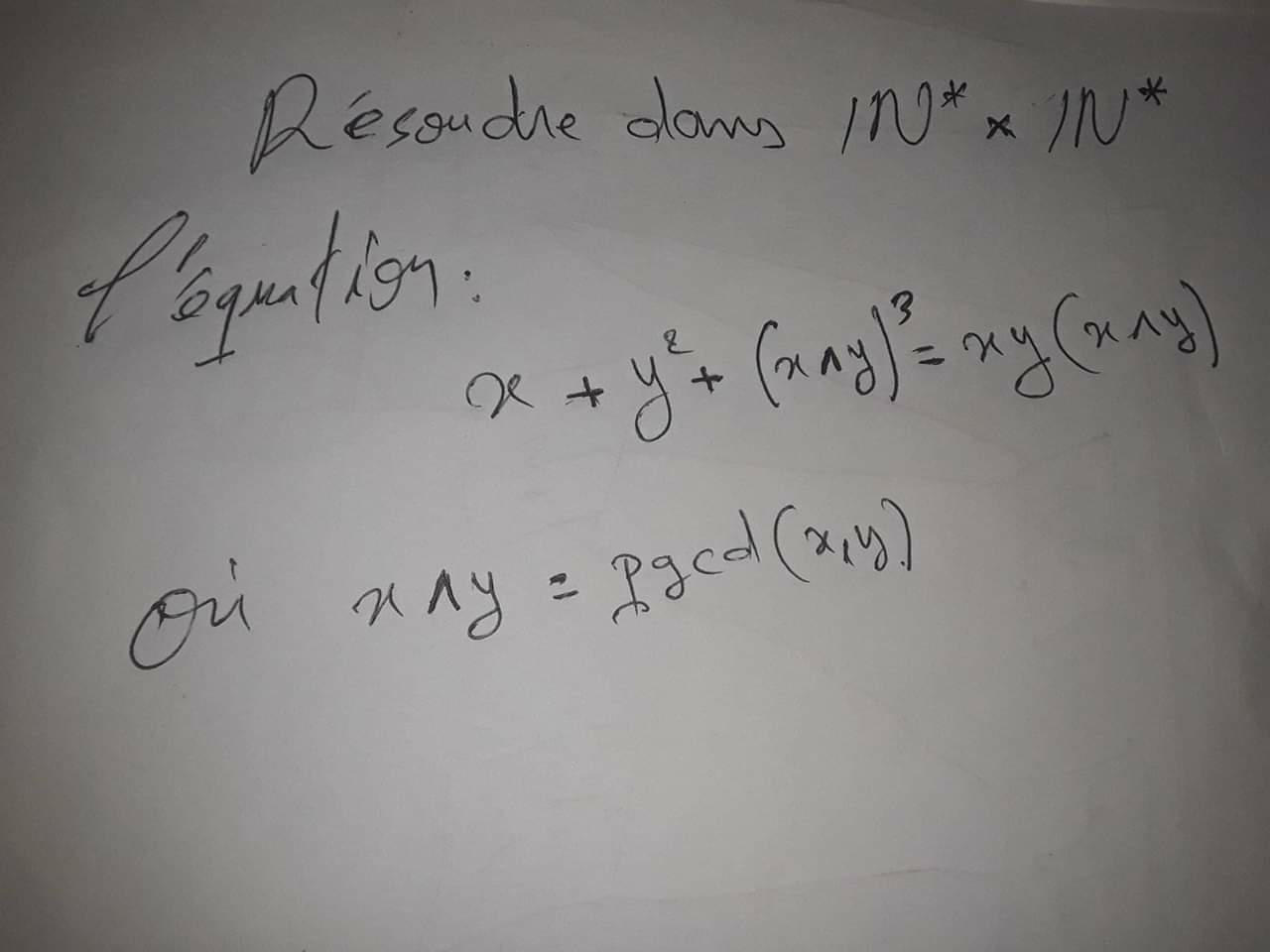
Commented by MJS last updated on 14/Jun/19
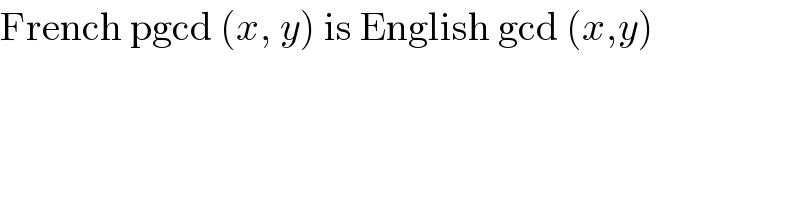
French pgcd (x, y) is English gcd (x,y)
$$\mathrm{French}\:\mathrm{pgcd}\:\left({x},\:{y}\right)\:\mathrm{is}\:\mathrm{English}\:\mathrm{gcd}\:\left({x},{y}\right) \\ $$
Commented by MJS last updated on 14/Jun/19
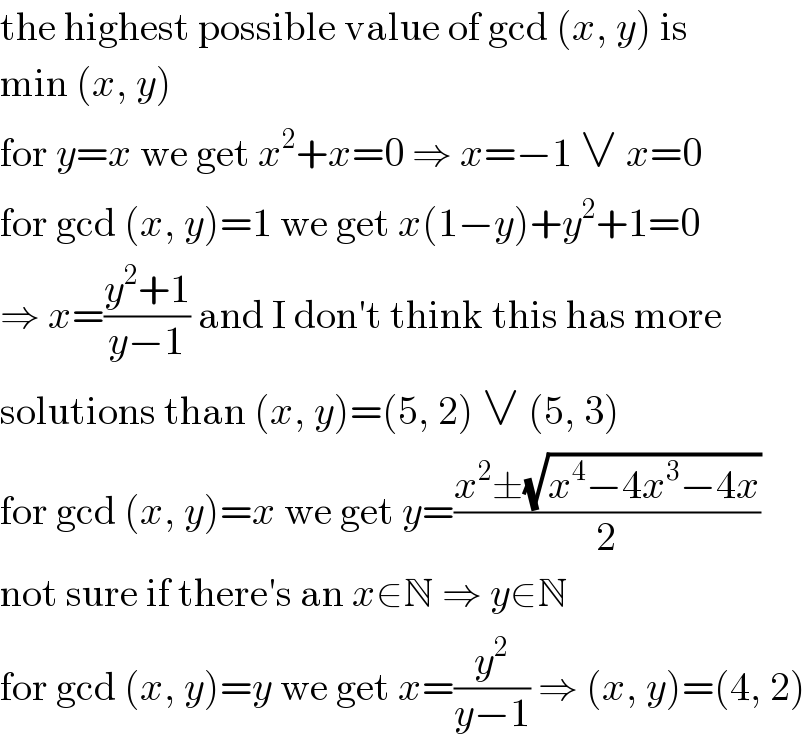
the highest possible value of gcd (x, y) is min (x, y) for y=x we get x^2 +x=0 ⇒ x=−1 ∨ x=0 for gcd (x, y)=1 we get x(1−y)+y^2 +1=0 ⇒ x=((y^2 +1)/(y−1)) and I don′t think this has more solutions than (x, y)=(5, 2) ∨ (5, 3) for gcd (x, y)=x we get y=((x^2 ±(√(x^4 −4x^3 −4x)))/2) not sure if there′s an x∈N ⇒ y∈N for gcd (x, y)=y we get x=(y^2 /(y−1)) ⇒ (x, y)=(4, 2)
$$\mathrm{the}\:\mathrm{highest}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{gcd}\:\left({x},\:{y}\right)\:\mathrm{is} \\ $$$$\mathrm{min}\:\left({x},\:{y}\right) \\ $$$$\mathrm{for}\:{y}={x}\:\mathrm{we}\:\mathrm{get}\:{x}^{\mathrm{2}} +{x}=\mathrm{0}\:\Rightarrow\:{x}=−\mathrm{1}\:\vee\:{x}=\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{gcd}\:\left({x},\:{y}\right)=\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:{x}\left(\mathrm{1}−{y}\right)+{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\frac{{y}^{\mathrm{2}} +\mathrm{1}}{{y}−\mathrm{1}}\:\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{has}\:\mathrm{more} \\ $$$$\mathrm{solutions}\:\mathrm{than}\:\left({x},\:{y}\right)=\left(\mathrm{5},\:\mathrm{2}\right)\:\vee\:\left(\mathrm{5},\:\mathrm{3}\right) \\ $$$$\mathrm{for}\:\mathrm{gcd}\:\left({x},\:{y}\right)={x}\:\mathrm{we}\:\mathrm{get}\:{y}=\frac{{x}^{\mathrm{2}} \pm\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4}{x}}}{\mathrm{2}} \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{an}\:{x}\in\mathbb{N}\:\Rightarrow\:{y}\in\mathbb{N} \\ $$$$\mathrm{for}\:\mathrm{gcd}\:\left({x},\:{y}\right)={y}\:\mathrm{we}\:\mathrm{get}\:{x}=\frac{{y}^{\mathrm{2}} }{{y}−\mathrm{1}}\:\Rightarrow\:\left({x},\:{y}\right)=\left(\mathrm{4},\:\mathrm{2}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 15/Jun/19
Thanks sir MJ^( ⧫) S!
$$\mathrm{Thanks}\:\mathrm{sir}\:\mathrm{M}\overset{\:\blacklozenge} {\mathbb{J}}\mathrm{S}! \\ $$
Answered by MJS last updated on 14/Jun/19
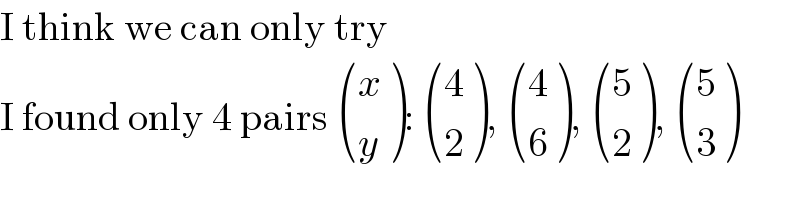
I think we can only try I found only 4 pairs ((x),(y) ): ((4),(2) ), ((4),(6) ), ((5),(2) ), ((5),(3) )
$$\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try} \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{only}\:\mathrm{4}\:\mathrm{pairs}\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}:\:\begin{pmatrix}{\mathrm{4}}\\{\mathrm{2}}\end{pmatrix},\:\begin{pmatrix}{\mathrm{4}}\\{\mathrm{6}}\end{pmatrix},\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{2}}\end{pmatrix},\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Jun/19
Sir, can we determine number of all such pairs?
$$\mathrm{Sir},\:\mathrm{can}\:\mathrm{we}\:\mathrm{determine}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{all}\:\mathrm{such}\:\mathrm{pairs}? \\ $$
Commented by MJS last updated on 14/Jun/19
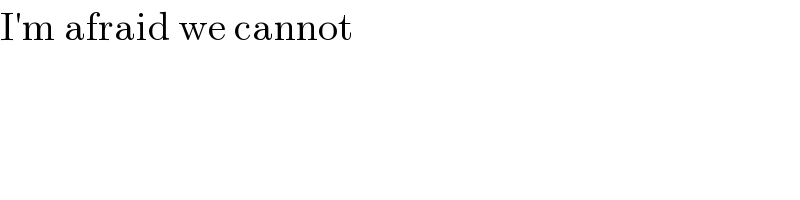
I′m afraid we cannot
$$\mathrm{I}'\mathrm{m}\:\mathrm{afraid}\:\mathrm{we}\:\mathrm{cannot} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jun/19
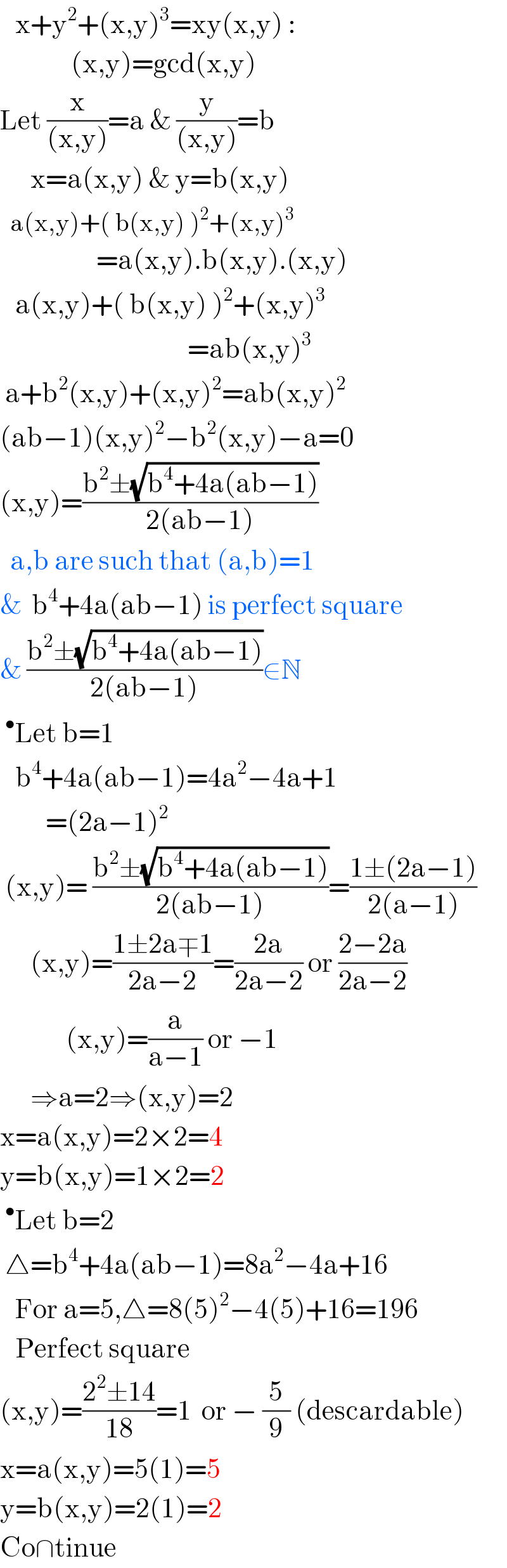
x+y^2 +(x,y)^3 =xy(x,y) : (x,y)=gcd(x,y) Let (x/((x,y)))=a & (y/((x,y)))=b x=a(x,y) & y=b(x,y) a(x,y)+( b(x,y) )^2 +(x,y)^3 =a(x,y).b(x,y).(x,y) a(x,y)+( b(x,y) )^2 +(x,y)^3 =ab(x,y)^3 a+b^2 (x,y)+(x,y)^2 =ab(x,y)^2 (ab−1)(x,y)^2 −b^2 (x,y)−a=0 (x,y)=((b^2 ±(√(b^4 +4a(ab−1))))/(2(ab−1))) a,b are such that (a,b)=1 & b^4 +4a(ab−1) is perfect square & ((b^2 ±(√(b^4 +4a(ab−1))))/(2(ab−1)))∈N ^• Let b=1 b^4 +4a(ab−1)=4a^2 −4a+1 =(2a−1)^2 (x,y)= ((b^2 ±(√(b^4 +4a(ab−1))))/(2(ab−1)))=((1±(2a−1))/(2(a−1))) (x,y)=((1±2a∓1)/(2a−2))=((2a)/(2a−2)) or ((2−2a)/(2a−2)) (x,y)=(a/(a−1)) or −1 ⇒a=2⇒(x,y)=2 x=a(x,y)=2×2=4 y=b(x,y)=1×2=2 ^• Let b=2 △=b^4 +4a(ab−1)=8a^2 −4a+16 For a=5,△=8(5)^2 −4(5)+16=196 Perfect square (x,y)=((2^2 ±14)/(18))=1 or − (5/9) (descardable) x=a(x,y)=5(1)=5 y=b(x,y)=2(1)=2 Co∩tinue
$$\:\:\:\mathrm{x}+\mathrm{y}^{\mathrm{2}} +\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{3}} =\mathrm{xy}\left(\mathrm{x},\mathrm{y}\right)\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x},\mathrm{y}\right)=\mathrm{gcd}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{Let}\:\frac{\mathrm{x}}{\left(\mathrm{x},\mathrm{y}\right)}=\mathrm{a}\:\&\:\frac{\mathrm{y}}{\left(\mathrm{x},\mathrm{y}\right)}=\mathrm{b}\: \\ $$$$\:\:\:\:\:\:\mathrm{x}=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)\:\&\:\mathrm{y}=\mathrm{b}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\:\:\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)+\left(\:\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)\:\right)^{\mathrm{2}} +\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right).\mathrm{b}\left(\mathrm{x},\mathrm{y}\right).\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\:\:\:\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)+\left(\:\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)\:\right)^{\mathrm{2}} +\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{ab}\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{3}} \\ $$$$\:\mathrm{a}+\mathrm{b}^{\mathrm{2}} \left(\mathrm{x},\mathrm{y}\right)+\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{2}} =\mathrm{ab}\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{ab}−\mathrm{1}\right)\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \left(\mathrm{x},\mathrm{y}\right)−\mathrm{a}=\mathrm{0} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\frac{\mathrm{b}^{\mathrm{2}} \pm\sqrt{\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{ab}−\mathrm{1}\right)} \\ $$$$\:\:\mathrm{a},\mathrm{b}\:\mathrm{are}\:\mathrm{such}\:\mathrm{that}\:\left(\mathrm{a},\mathrm{b}\right)=\mathrm{1} \\ $$$$\&\:\:\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)\:\mathrm{is}\:\mathrm{perfect}\:\mathrm{square} \\ $$$$\&\:\frac{\mathrm{b}^{\mathrm{2}} \pm\sqrt{\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{ab}−\mathrm{1}\right)}\in\mathbb{N} \\ $$$$\:^{\bullet} \mathrm{Let}\:\mathrm{b}=\mathrm{1}\: \\ $$$$\:\:\:\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)=\mathrm{4a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{2a}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\left(\mathrm{x},\mathrm{y}\right)=\:\frac{\mathrm{b}^{\mathrm{2}} \pm\sqrt{\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{ab}−\mathrm{1}\right)}=\frac{\mathrm{1}\pm\left(\mathrm{2a}−\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{a}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\left(\mathrm{x},\mathrm{y}\right)=\frac{\mathrm{1}\pm\mathrm{2a}\mp\mathrm{1}}{\mathrm{2a}−\mathrm{2}}=\frac{\mathrm{2a}}{\mathrm{2a}−\mathrm{2}}\:\mathrm{or}\:\frac{\mathrm{2}−\mathrm{2a}}{\mathrm{2a}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x},\mathrm{y}\right)=\frac{\mathrm{a}}{\mathrm{a}−\mathrm{1}}\:\mathrm{or}\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{a}=\mathrm{2}\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2}×\mathrm{2}=\mathrm{4} \\ $$$$\mathrm{y}=\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{1}×\mathrm{2}=\mathrm{2} \\ $$$$\:^{\bullet} \mathrm{Let}\:\mathrm{b}=\mathrm{2} \\ $$$$\:\bigtriangleup=\mathrm{b}^{\mathrm{4}} +\mathrm{4a}\left(\mathrm{ab}−\mathrm{1}\right)=\mathrm{8a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{16} \\ $$$$\:\:\:\mathrm{For}\:\mathrm{a}=\mathrm{5},\bigtriangleup=\mathrm{8}\left(\mathrm{5}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}\right)+\mathrm{16}=\mathrm{196} \\ $$$$\:\:\:\mathrm{Perfect}\:\mathrm{square} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\frac{\mathrm{2}^{\mathrm{2}} \pm\mathrm{14}}{\mathrm{18}}=\mathrm{1}\:\:\mathrm{or}\:−\:\frac{\mathrm{5}}{\mathrm{9}}\:\left(\mathrm{descardable}\right) \\ $$$$\mathrm{x}=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{5}\left(\mathrm{1}\right)=\mathrm{5} \\ $$$$\mathrm{y}=\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$\mathrm{Co}\cap\mathrm{tinue} \\ $$
Commented by aliesam last updated on 14/Jun/19
good bless sir
$${good}\:{bless}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Jun/19
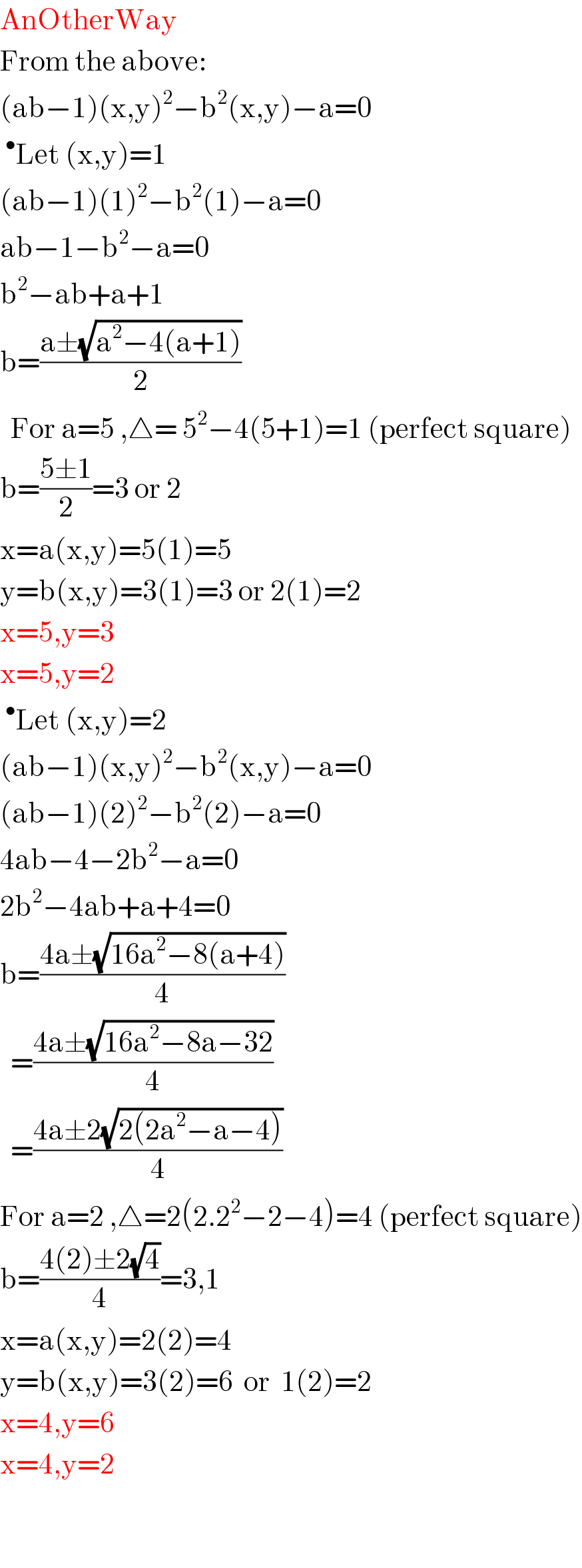
AnOtherWay From the above: (ab−1)(x,y)^2 −b^2 (x,y)−a=0 ^• Let (x,y)=1 (ab−1)(1)^2 −b^2 (1)−a=0 ab−1−b^2 −a=0 b^2 −ab+a+1 b=((a±(√(a^2 −4(a+1))))/2) For a=5 ,△= 5^2 −4(5+1)=1 (perfect square) b=((5±1)/2)=3 or 2 x=a(x,y)=5(1)=5 y=b(x,y)=3(1)=3 or 2(1)=2 x=5,y=3 x=5,y=2 ^• Let (x,y)=2 (ab−1)(x,y)^2 −b^2 (x,y)−a=0 (ab−1)(2)^2 −b^2 (2)−a=0 4ab−4−2b^2 −a=0 2b^2 −4ab+a+4=0 b=((4a±(√(16a^2 −8(a+4))))/4) =((4a±(√(16a^2 −8a−32)))/4) =((4a±2(√(2(2a^2 −a−4))))/4) For a=2 ,△=2(2.2^2 −2−4)=4 (perfect square) b=((4(2)±2(√4))/4)=3,1 x=a(x,y)=2(2)=4 y=b(x,y)=3(2)=6 or 1(2)=2 x=4,y=6 x=4,y=2
$$\mathrm{AnOtherWay} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{above}: \\ $$$$\left(\mathrm{ab}−\mathrm{1}\right)\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \left(\mathrm{x},\mathrm{y}\right)−\mathrm{a}=\mathrm{0} \\ $$$$\:^{\bullet} \mathrm{Let}\:\left(\mathrm{x},\mathrm{y}\right)=\mathrm{1} \\ $$$$\left(\mathrm{ab}−\mathrm{1}\right)\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \left(\mathrm{1}\right)−\mathrm{a}=\mathrm{0} \\ $$$$\mathrm{ab}−\mathrm{1}−\mathrm{b}^{\mathrm{2}} −\mathrm{a}=\mathrm{0} \\ $$$$\mathrm{b}^{\mathrm{2}} −\mathrm{ab}+\mathrm{a}+\mathrm{1} \\ $$$$\mathrm{b}=\frac{\mathrm{a}\pm\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{a}+\mathrm{1}\right)}}{\mathrm{2}} \\ $$$$\:\:\mathrm{For}\:\mathrm{a}=\mathrm{5}\:,\bigtriangleup=\:\mathrm{5}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}+\mathrm{1}\right)=\mathrm{1}\:\left(\mathrm{perfect}\:\mathrm{square}\right) \\ $$$$\mathrm{b}=\frac{\mathrm{5}\pm\mathrm{1}}{\mathrm{2}}=\mathrm{3}\:\mathrm{or}\:\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{5}\left(\mathrm{1}\right)=\mathrm{5} \\ $$$$\mathrm{y}=\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{3}\left(\mathrm{1}\right)=\mathrm{3}\:\mathrm{or}\:\mathrm{2}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{5},\mathrm{y}=\mathrm{3} \\ $$$$\mathrm{x}=\mathrm{5},\mathrm{y}=\mathrm{2} \\ $$$$\:^{\bullet} \mathrm{Let}\:\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2} \\ $$$$\left(\mathrm{ab}−\mathrm{1}\right)\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \left(\mathrm{x},\mathrm{y}\right)−\mathrm{a}=\mathrm{0} \\ $$$$\left(\mathrm{ab}−\mathrm{1}\right)\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{a}=\mathrm{0} \\ $$$$\mathrm{4ab}−\mathrm{4}−\mathrm{2b}^{\mathrm{2}} −\mathrm{a}=\mathrm{0} \\ $$$$\mathrm{2b}^{\mathrm{2}} −\mathrm{4ab}+\mathrm{a}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{b}=\frac{\mathrm{4a}\pm\sqrt{\mathrm{16a}^{\mathrm{2}} −\mathrm{8}\left(\mathrm{a}+\mathrm{4}\right)}}{\mathrm{4}} \\ $$$$\:\:=\frac{\mathrm{4a}\pm\sqrt{\mathrm{16a}^{\mathrm{2}} −\mathrm{8a}−\mathrm{32}}}{\mathrm{4}} \\ $$$$\:\:=\frac{\mathrm{4a}\pm\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{a}−\mathrm{4}\right)}}{\mathrm{4}} \\ $$$$\mathrm{For}\:\mathrm{a}=\mathrm{2}\:,\bigtriangleup=\mathrm{2}\left(\mathrm{2}.\mathrm{2}^{\mathrm{2}} −\mathrm{2}−\mathrm{4}\right)=\mathrm{4}\:\left(\mathrm{perfect}\:\mathrm{square}\right) \\ $$$$\mathrm{b}=\frac{\mathrm{4}\left(\mathrm{2}\right)\pm\mathrm{2}\sqrt{\mathrm{4}}}{\mathrm{4}}=\mathrm{3},\mathrm{1} \\ $$$$\mathrm{x}=\mathrm{a}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2}\left(\mathrm{2}\right)=\mathrm{4} \\ $$$$\mathrm{y}=\mathrm{b}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{3}\left(\mathrm{2}\right)=\mathrm{6}\:\:\mathrm{or}\:\:\mathrm{1}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{4},\mathrm{y}=\mathrm{6} \\ $$$$\mathrm{x}=\mathrm{4},\mathrm{y}=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 14/Jun/19
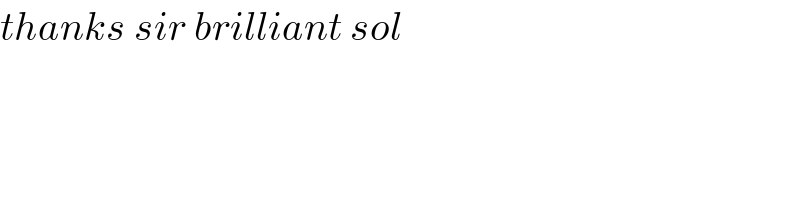
thanks sir brilliant sol
$${thanks}\:{sir}\:{brilliant}\:{sol} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Jun/19
You′re welcome sir!
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 15/Jun/19
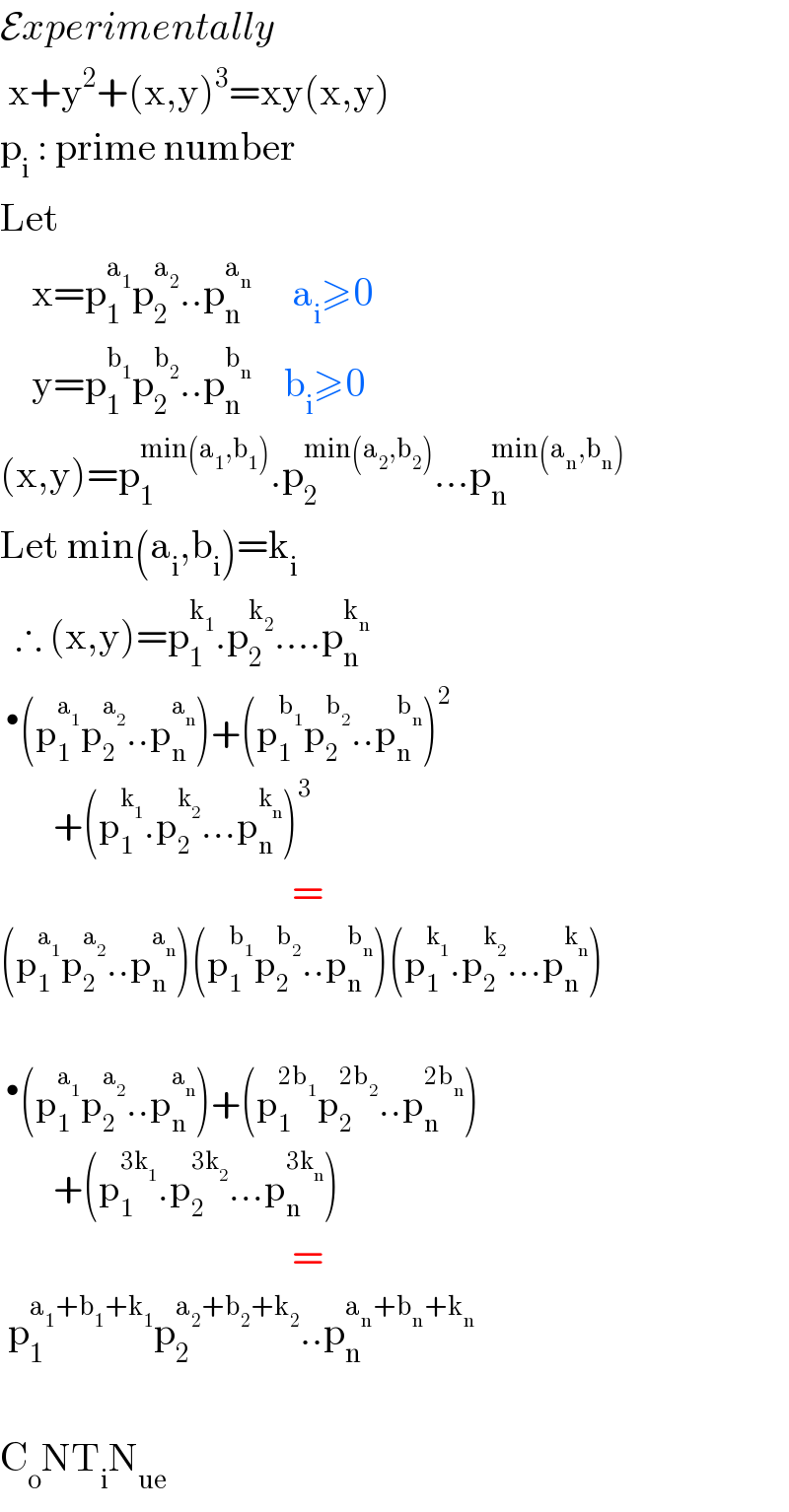
Experimentally x+y^2 +(x,y)^3 =xy(x,y) p_i : prime number Let x=p_1 ^a_1 p_2 ^a_2 ..p_n ^a_n a_i ≥0 y=p_1 ^b_1 p_2 ^b_2 ..p_n ^b_n b_i ≥0 (x,y)=p_1 ^(min(a_1 ,b_1 )) .p_2 ^(min(a_2 ,b_2 )) ...p_n ^(min(a_n ,b_n )) Let min(a_i ,b_i )=k_i ∴ (x,y)=p_1 ^k_1 .p_2 ^k_2 ....p_n ^k_n ^• (p_1 ^a_1 p_2 ^a_2 ..p_n ^a_n )+(p_1 ^b_1 p_2 ^b_2 ..p_n ^b_n )^2 +(p_1 ^k_1 .p_2 ^k_2 ...p_n ^k_n )^3 = (p_1 ^a_1 p_2 ^a_2 ..p_n ^a_n )(p_1 ^b_1 p_2 ^b_2 ..p_n ^b_n )(p_1 ^k_1 .p_2 ^k_2 ...p_n ^k_n ) ^• (p_1 ^a_1 p_2 ^a_2 ..p_n ^a_n )+(p_1 ^(2b_1 ) p_2 ^(2b_2 ) ..p_n ^(2b_n ) ) +(p_1 ^(3k_1 ) .p_2 ^(3k_2 ) ...p_n ^(3k_n ) ) = p_1 ^(a_1 +b_1 +k_1 ) p_2 ^(a_2 +b_2 +k_2 ) ..p_n ^(a_n +b_n +k_n ) C_o NT_i N_(ue)
$$\mathcal{E}{xperimentally} \\ $$$$\:\mathrm{x}+\mathrm{y}^{\mathrm{2}} +\left(\mathrm{x},\mathrm{y}\right)^{\mathrm{3}} =\mathrm{xy}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{p}_{\mathrm{i}} \::\:\mathrm{prime}\:\mathrm{number} \\ $$$$\mathrm{Let} \\ $$$$\:\:\:\:\mathrm{x}=\mathrm{p}_{\mathrm{1}} ^{\mathrm{a}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{a}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{a}_{\mathrm{n}} } \:\:\:\:\:\mathrm{a}_{\mathrm{i}} \geqslant\mathrm{0} \\ $$$$\:\:\:\:\mathrm{y}=\mathrm{p}_{\mathrm{1}} ^{\mathrm{b}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{b}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{b}_{\mathrm{n}} } \:\:\:\:\mathrm{b}_{\mathrm{i}} \geqslant\mathrm{0} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\mathrm{p}_{\mathrm{1}} ^{\mathrm{min}\left(\mathrm{a}_{\mathrm{1}} ,\mathrm{b}_{\mathrm{1}} \right)} .\mathrm{p}_{\mathrm{2}} ^{\mathrm{min}\left(\mathrm{a}_{\mathrm{2}} ,\mathrm{b}_{\mathrm{2}} \right)} …\mathrm{p}_{\mathrm{n}} ^{\mathrm{min}\left(\mathrm{a}_{\mathrm{n}} ,\mathrm{b}_{\mathrm{n}} \right)} \\ $$$$\mathrm{Let}\:\mathrm{min}\left(\mathrm{a}_{\mathrm{i}} ,\mathrm{b}_{\mathrm{i}} \right)=\mathrm{k}_{\mathrm{i}} \\ $$$$\:\:\therefore\:\left(\mathrm{x},\mathrm{y}\right)=\mathrm{p}_{\mathrm{1}} ^{\mathrm{k}_{\mathrm{1}} } .\mathrm{p}_{\mathrm{2}} ^{\mathrm{k}_{\mathrm{2}} } ….\mathrm{p}_{\mathrm{n}} ^{\mathrm{k}_{\mathrm{n}} } \\ $$$$\:^{\bullet} \left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{a}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{a}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{a}_{\mathrm{n}} } \right)+\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{b}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{b}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{b}_{\mathrm{n}} } \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{k}_{\mathrm{1}} } .\mathrm{p}_{\mathrm{2}} ^{\mathrm{k}_{\mathrm{2}} } …\mathrm{p}_{\mathrm{n}} ^{\mathrm{k}_{\mathrm{n}} } \right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:= \\ $$$$\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{a}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{a}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{a}_{\mathrm{n}} } \right)\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{b}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{b}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{b}_{\mathrm{n}} } \right)\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{k}_{\mathrm{1}} } .\mathrm{p}_{\mathrm{2}} ^{\mathrm{k}_{\mathrm{2}} } …\mathrm{p}_{\mathrm{n}} ^{\mathrm{k}_{\mathrm{n}} } \right) \\ $$$$ \\ $$$$\:^{\bullet} \left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{a}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{a}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{a}_{\mathrm{n}} } \right)+\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{2b}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{2b}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{2b}_{\mathrm{n}} } \right) \\ $$$$\:\:\:\:\:\:\:\:\:+\left(\mathrm{p}_{\mathrm{1}} ^{\mathrm{3k}_{\mathrm{1}} } .\mathrm{p}_{\mathrm{2}} ^{\mathrm{3k}_{\mathrm{2}} } …\mathrm{p}_{\mathrm{n}} ^{\mathrm{3k}_{\mathrm{n}} } \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:= \\ $$$$\:\mathrm{p}_{\mathrm{1}} ^{\mathrm{a}_{\mathrm{1}} +\mathrm{b}_{\mathrm{1}} +\mathrm{k}_{\mathrm{1}} } \mathrm{p}_{\mathrm{2}} ^{\mathrm{a}_{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} +\mathrm{k}_{\mathrm{2}} } ..\mathrm{p}_{\mathrm{n}} ^{\mathrm{a}_{\mathrm{n}} +\mathrm{b}_{\mathrm{n}} +\mathrm{k}_{\mathrm{n}} } \\ $$$$ \\ $$$$\mathrm{C}_{\mathrm{o}} \mathrm{NT}_{\mathrm{i}} \mathrm{N}_{\mathrm{ue}} \\ $$
Commented by aliesam last updated on 15/Jun/19
you are graet sir thank you
$${you}\:{are}\:{graet}\:{sir}\:{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *