Menu Close

Question-62088

Tinku Tara 0 Comments
Pin




Question Number 62088 by Cypher1207 last updated on 15/Jun/19
Commented by Cypher1207 last updated on 15/Jun/19
(very)^2 easy....
$$\left({very}\right)^{\mathrm{2}} {easy}…. \\ $$
Commented by maxmathsup by imad last updated on 15/Jun/19
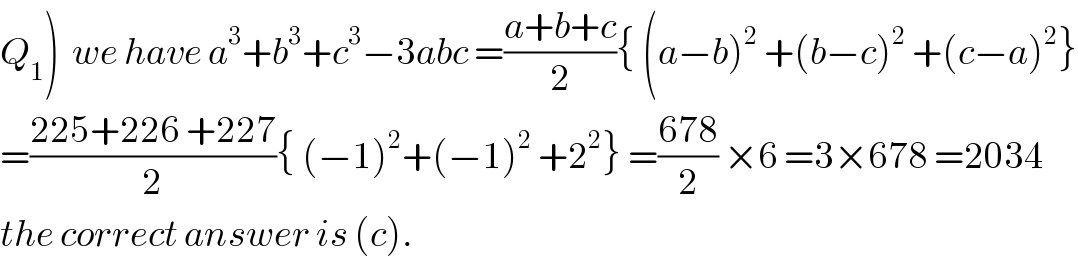
Q_1 ) we have a^3 +b^3 +c^3 −3abc =((a+b+c)/2){ (a−b)^2 +(b−c)^2 +(c−a)^2 } =((225+226 +227)/2){ (−1)^2 +(−1)^2 +2^2 } =((678)/2) ×6 =3×678 =2034 the correct answer is (c).
$$\left.{Q}_{\mathrm{1}} \right)\:\:{we}\:{have}\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\:=\frac{{a}+{b}+{c}}{\mathrm{2}}\left\{\:\left({a}−{b}\right)^{\mathrm{2}} \:+\left({b}−{c}\right)^{\mathrm{2}} \:+\left({c}−{a}\right)^{\mathrm{2}} \right\} \\ $$$$=\frac{\mathrm{225}+\mathrm{226}\:+\mathrm{227}}{\mathrm{2}}\left\{\:\left(−\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{2}} \right\}\:=\frac{\mathrm{678}}{\mathrm{2}}\:×\mathrm{6}\:=\mathrm{3}×\mathrm{678}\:=\mathrm{2034} \\ $$$${the}\:{correct}\:{answer}\:{is}\:\left({c}\right). \\ $$
Commented by maxmathsup by imad last updated on 15/Jun/19
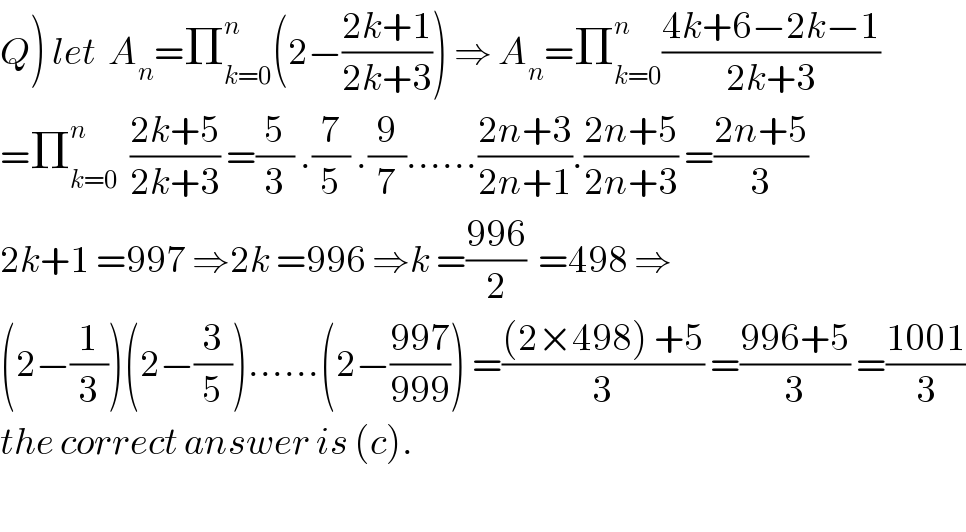
Q) let A_n =Π_(k=0) ^n (2−((2k+1)/(2k+3))) ⇒ A_n =Π_(k=0) ^n ((4k+6−2k−1)/(2k+3)) =Π_(k=0) ^n ((2k+5)/(2k+3)) =(5/3) .(7/5) .(9/7)......((2n+3)/(2n+1)).((2n+5)/(2n+3)) =((2n+5)/3) 2k+1 =997 ⇒2k =996 ⇒k =((996)/2) =498 ⇒ (2−(1/3))(2−(3/5))......(2−((997)/(999))) =(((2×498) +5)/3) =((996+5)/3) =((1001)/3) the correct answer is (c).
$$\left.{Q}\right)\:{let}\:\:{A}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{2}−\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\right)\:\Rightarrow\:{A}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \frac{\mathrm{4}{k}+\mathrm{6}−\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}} \\ $$$$=\prod_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{2}{k}+\mathrm{5}}{\mathrm{2}{k}+\mathrm{3}}\:=\frac{\mathrm{5}}{\mathrm{3}}\:.\frac{\mathrm{7}}{\mathrm{5}}\:.\frac{\mathrm{9}}{\mathrm{7}}……\frac{\mathrm{2}{n}+\mathrm{3}}{\mathrm{2}{n}+\mathrm{1}}.\frac{\mathrm{2}{n}+\mathrm{5}}{\mathrm{2}{n}+\mathrm{3}}\:=\frac{\mathrm{2}{n}+\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{2}{k}+\mathrm{1}\:=\mathrm{997}\:\Rightarrow\mathrm{2}{k}\:=\mathrm{996}\:\Rightarrow{k}\:=\frac{\mathrm{996}}{\mathrm{2}}\:\:=\mathrm{498}\:\Rightarrow \\ $$$$\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{2}−\frac{\mathrm{3}}{\mathrm{5}}\right)……\left(\mathrm{2}−\frac{\mathrm{997}}{\mathrm{999}}\right)\:=\frac{\left(\mathrm{2}×\mathrm{498}\right)\:+\mathrm{5}}{\mathrm{3}}\:=\frac{\mathrm{996}+\mathrm{5}}{\mathrm{3}}\:=\frac{\mathrm{1001}}{\mathrm{3}} \\ $$$${the}\:{correct}\:{answer}\:{is}\:\left({c}\right). \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *