Question Number 62102 by rajesh4661kumar@gamil.com last updated on 15/Jun/19
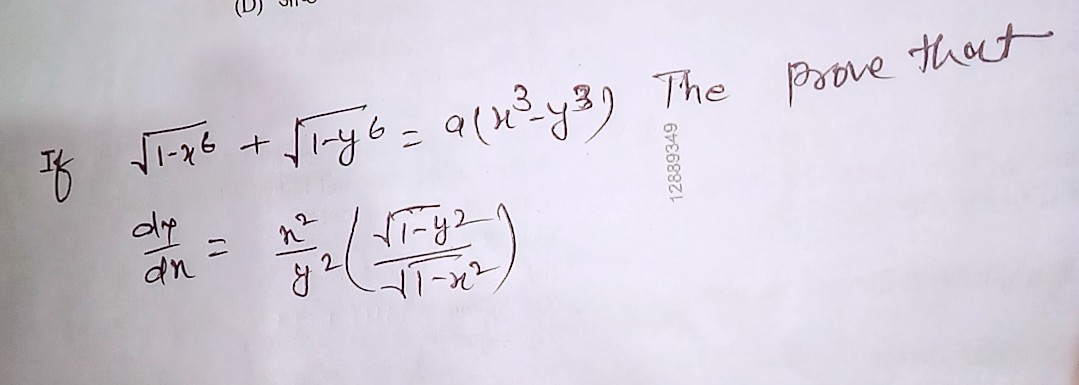
Answered by Kunal12588 last updated on 15/Jun/19
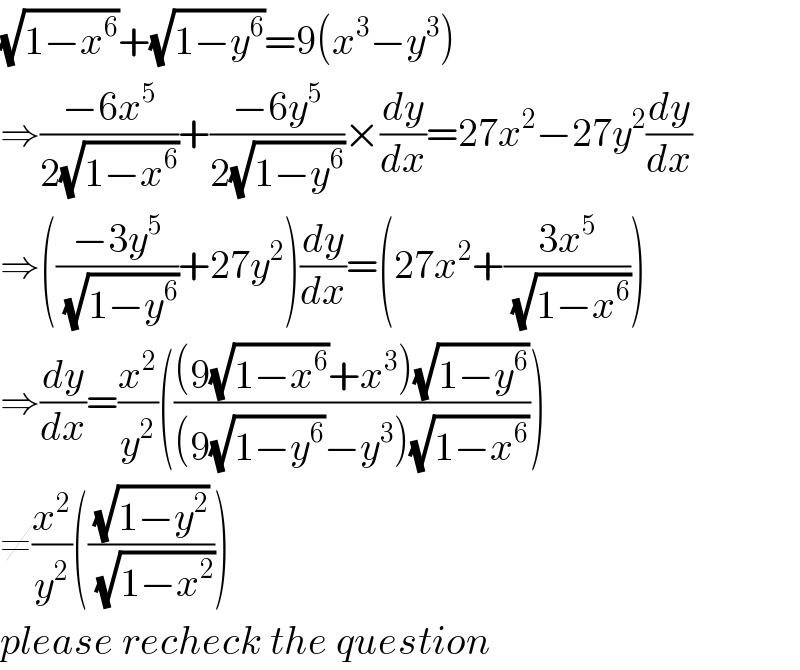
$$\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }+\sqrt{\mathrm{1}−{y}^{\mathrm{6}} }=\mathrm{9}\left({x}^{\mathrm{3}} −{y}^{\mathrm{3}} \right) \\ $$$$\Rightarrow\frac{−\mathrm{6}{x}^{\mathrm{5}} }{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }}+\frac{−\mathrm{6}{y}^{\mathrm{5}} }{\mathrm{2}\sqrt{\mathrm{1}−{y}^{\mathrm{6}} }}×\frac{{dy}}{{dx}}=\mathrm{27}{x}^{\mathrm{2}} −\mathrm{27}{y}^{\mathrm{2}} \frac{{dy}}{{dx}} \\ $$$$\Rightarrow\left(\frac{−\mathrm{3}{y}^{\mathrm{5}} }{\:\sqrt{\mathrm{1}−{y}^{\mathrm{6}} }}+\mathrm{27}{y}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}=\left(\mathrm{27}{x}^{\mathrm{2}} +\frac{\mathrm{3}{x}^{\mathrm{5}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }}\right) \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\left(\frac{\left(\mathrm{9}\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }+{x}^{\mathrm{3}} \right)\sqrt{\mathrm{1}−{y}^{\mathrm{6}} }}{\left(\mathrm{9}\sqrt{\mathrm{1}−{y}^{\mathrm{6}} }−{y}^{\mathrm{3}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }}\right) \\ $$$$\neq\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\left(\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right) \\ $$$${please}\:{recheck}\:{the}\:{question} \\ $$
