Menu Close

Question-62232

Tinku Tara 0 Comments
Pin




Question Number 62232 by aliesam last updated on 18/Jun/19
Commented by maxmathsup by imad last updated on 18/Jun/19
we have ∣α+β e^(iθ) ∣ =∣α +βcosθ +iβsinθ∣ =(√((α+βcosθ)^2 +β^2 sin^2 θ)) ⇒ ln(∣α+ie^(iθ) ∣) =(1/2)ln{ (α+β cosθ)^2 +β^2 sin^2 θ} =(1/2)ln{α^2 +2αβ cosθ +β^2 } ⇒ I =(1/2) ∫_0 ^(2π) ln( α^2 +β^2 +2αβ cosθ)dθ =(1/2) ∫_0 ^(2π) {ln(α^2 +β^2 ) +ln(1+((2αβ)/(α^2 +β^2 )) cosθ)}dθ =πln(α^2 +β^2 ) +(1/2) ∫_0 ^(2π) ln(1+((2αβ)/(α^2 +β^2 )) cosθ)dθ let find f(t) =∫_0 ^(2π) ln(1+tcosθ)dθ ⇒f^′ (t) =∫_0 ^(2π) ((cosθ)/(1+tcosθ)) dθ =(1/t) ∫_0 ^(2π) ((1+tcosθ−1)/(1+tcosθ)) dθ =((2π)/t) −(1/t) ∫_0 ^(2π) (dθ/(1+tcosθ)) changement e^(iθ) =z give ∫_0 ^(2π) (dθ/(1+t cosθ)) =∫_(∣z∣=1) (1/(1+t((z+z^(−1) )/2))) (dz/(iz)) =∫_(∣z∣=1) ((2dz)/(iz(2 +tz +tz^(−1) ))) =∫_(∣z∣=1) ((−2idz)/(2z +tz^2 +t)) =∫_(∣z∣=1) ((−2idz)/(tz^2 +2z +t)) let w(z) =((−2i)/(tz^2 +2z +t)) poles of w? Δ^′ =1−t^2 case 1 ∣t∣<1 ⇒ z_1 =−1+(√(1−t^2 )) and z_2 =−1−(√(1−t^2 )) ∣z_1 ∣ −1 =∣−1+(√(1−t^2 ))∣−1 =1−(√(1−t^2 ))−1 <0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1 =∣−1−(√(1−t^2 ))∣−1 =1+(√(1−t^2 ))−1 >0 ( to eliminate from residus) ∫_(∣z∣=1) w−z)dz =2iπ Res(w,z_1 ) but w(z) =((−2i)/(t(z−z_1 )(z−z_2 ))) ⇒ Res(w,z_1 ) =((−2i)/(t(z_1 −z_2 ))) =((−2i)/(t2(√(1−t^2 )))) =((−i)/(t(√(1−t^2 )))) ⇒ ∫_(∣z∣=1) w(z)dz =2iπ (((−i)/(t(√(1−t^2 ))))) =((2π)/(t(√(1−t^2 )))) ⇒ f^′ (t) = ((2π)/t) −((2π)/(t^2 (√(1−t^2 )))) ⇒f(t) =2πln∣t∣ −2π ∫ (dt/(t^2 (√(1−t^2 )))) +c ∫ (dt/(t^2 (√(1−t^2 )))) =∫ (1/t^2 )(1−t^2 )^((−1)/2) dt =_(by parts) −(1/t)(1−t^2 )^(−(1/2)) −∫ −(1/t)(−(1/2))(−2t)(1−t^2 )^(−(3/2)) dt =−(1/(t(√(1−t^2 )))) + ∫ (1/((1−t^2 )^(3/2) )) dt cyangement t =sinα give ∫ (dt/((1−t^2 )^(3/2) )) =∫ (1/(cos^3 α)) cosα dα =∫ (dα/(cos^2 α)) =∫ ((2dα)/(1+cos(2α))) =_(tan(α)=u) ∫ ((2du)/((1+u^2 )(1+((1−u^2 )/(1+u^2 ))))) =∫ ((2du)/(1+u^2 +1−u^2 )) =∫ du =u +c =tan(α)+c =tan(arcsint) +c ⇒ f(t) =2π ln∣t∣−2π {((−1)/(t(√(1−t^2 )))) +tan(arcsint)} +c ⇒ I =πln(α^2 +β^2 ) +(1/2)f(((2αβ)/(α^2 +β^2 )) ) +c I=πln(α^2 +β^2 ) +πln∣((2αβ)/(α^2 +β^2 ))∣−π{−(1/(((2αβ)/(α^2 +β^2 ))(√(1−(((2αβ)/(α^2 +β^( )))))^2 )) +tan(arcsin(((2αβ)/(α^2 +β^2 )))} +c rest to find the value of c ....be continued...
$${we}\:{have}\:\mid\alpha+\beta\:{e}^{{i}\theta} \mid\:=\mid\alpha\:+\beta{cos}\theta\:+{i}\beta{sin}\theta\mid\:=\sqrt{\left(\alpha+\beta{cos}\theta\right)^{\mathrm{2}} \:+\beta^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:\Rightarrow \\ $$$${ln}\left(\mid\alpha+{ie}^{{i}\theta} \mid\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\:\left(\alpha+\beta\:{cos}\theta\right)^{\mathrm{2}} \:+\beta^{\mathrm{2}} {sin}^{\mathrm{2}} \theta\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\alpha^{\mathrm{2}} +\mathrm{2}\alpha\beta\:{cos}\theta\:+\beta^{\mathrm{2}} \right\}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(\:\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \:+\mathrm{2}\alpha\beta\:{cos}\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left\{{ln}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\:+{ln}\left(\mathrm{1}+\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\:{cos}\theta\right)\right\}{d}\theta \\ $$$$=\pi{ln}\left(\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{ln}\left(\mathrm{1}+\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\:{cos}\theta\right){d}\theta\:\:{let}\:{find} \\ $$$${f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(\mathrm{1}+{tcos}\theta\right){d}\theta\:\:\:\:\Rightarrow{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{cos}\theta}{\mathrm{1}+{tcos}\theta}\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{1}+{tcos}\theta−\mathrm{1}}{\mathrm{1}+{tcos}\theta}\:{d}\theta\:=\frac{\mathrm{2}\pi}{{t}}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{d}\theta}{\mathrm{1}+{tcos}\theta} \\ $$$${changement}\:{e}^{{i}\theta} \:={z}\:{give}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{d}\theta}{\mathrm{1}+{t}\:{cos}\theta}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{dz}}{{iz}\left(\mathrm{2}\:+{tz}\:+{tz}^{−\mathrm{1}} \right)}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{−\mathrm{2}{idz}}{\mathrm{2}{z}\:+{tz}^{\mathrm{2}} \:+{t}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{−\mathrm{2}{idz}}{{tz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{t}} \\ $$$${let}\:{w}\left({z}\right)\:=\frac{−\mathrm{2}{i}}{{tz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{t}}\:\:{poles}\:{of}\:{w}? \\ $$$$\Delta^{'} \:=\mathrm{1}−{t}^{\mathrm{2}} \:\:\:{case}\:\mathrm{1}\:\:\:\:\mid{t}\mid<\mathrm{1}\:\Rightarrow\:{z}_{\mathrm{1}} =−\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:\:{and}\:{z}_{\mathrm{2}} =−\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\mid−\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\mid−\mathrm{1}\:=\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\mathrm{1}\:<\mathrm{0}\:\Rightarrow\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mid−\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\mid−\mathrm{1}\:=\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\mathrm{1}\:>\mathrm{0}\:\left(\:{to}\:{eliminate}\:{from}\:{residus}\right) \\ $$$$\left.\int_{\mid{z}\mid=\mathrm{1}} \:\:\:{w}−{z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({w},{z}_{\mathrm{1}} \right)\:\:\:{but}\:{w}\left({z}\right)\:=\frac{−\mathrm{2}{i}}{{t}\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${Res}\left({w},{z}_{\mathrm{1}} \right)\:=\frac{−\mathrm{2}{i}}{{t}\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)}\:=\frac{−\mathrm{2}{i}}{{t}\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:=\frac{−{i}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\:{w}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left(\frac{−{i}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right)\:=\frac{\mathrm{2}\pi}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\:\frac{\mathrm{2}\pi}{{t}}\:−\frac{\mathrm{2}\pi}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\Rightarrow{f}\left({t}\right)\:=\mathrm{2}\pi{ln}\mid{t}\mid\:−\mathrm{2}\pi\:\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:+{c}\: \\ $$$$\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:=\int\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \:{dt}\:=_{{by}\:{parts}} \:\:\:\:\:−\frac{\mathrm{1}}{{t}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:−\int\:−\frac{\mathrm{1}}{{t}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\mathrm{2}{t}\right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} {dt} \\ $$$$=−\frac{\mathrm{1}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:+\:\int\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dt}\:\:\:{cyangement}\:{t}\:={sin}\alpha\:{give} \\ $$$$\int\:\:\:\frac{{dt}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\int\:\:\frac{\mathrm{1}}{{cos}^{\mathrm{3}} \alpha}\:{cos}\alpha\:{d}\alpha\:=\int\:\:\frac{{d}\alpha}{{cos}^{\mathrm{2}} \alpha}\:=\int\:\:\:\frac{\mathrm{2}{d}\alpha}{\mathrm{1}+{cos}\left(\mathrm{2}\alpha\right)} \\ $$$$=_{{tan}\left(\alpha\right)={u}} \:\:\:\:\:\:\:\int\:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)}\:=\int\:\:\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }\:=\int\:{du}\:={u}\:+{c} \\ $$$$={tan}\left(\alpha\right)+{c}\:={tan}\left({arcsint}\right)\:+{c}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\mathrm{2}\pi\:{ln}\mid{t}\mid−\mathrm{2}\pi\:\left\{\frac{−\mathrm{1}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:+{tan}\left({arcsint}\right)\right\}\:+{c}\:\Rightarrow \\ $$$${I}\:=\pi{ln}\left(\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\:+\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\:\right)\:+{c} \\ $$$${I}=\pi{ln}\left(\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\:+\pi{ln}\mid\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\mid−\pi\left\{−\frac{\mathrm{1}}{\left.\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\left(\right.} }\right.}\right)^{\mathrm{2}} }\:+{tan}\left({arcsin}\left(\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\right)\right\}\right. \\ $$$$+{c}\:\:\:{rest}\:{to}\:{find}\:\:{the}\:{value}\:{of}\:{c}\:\:\:….{be}\:{continued}… \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 18/Jun/19
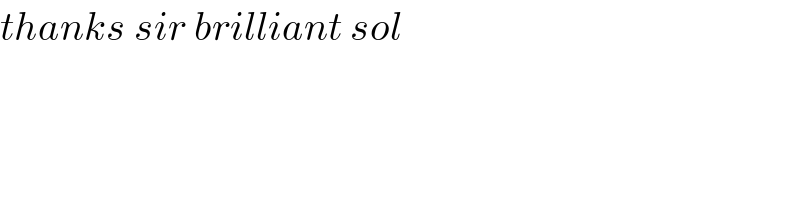
thanks sir brilliant sol
$${thanks}\:{sir}\:{brilliant}\:{sol} \\ $$
Commented by maxmathsup by imad last updated on 18/Jun/19
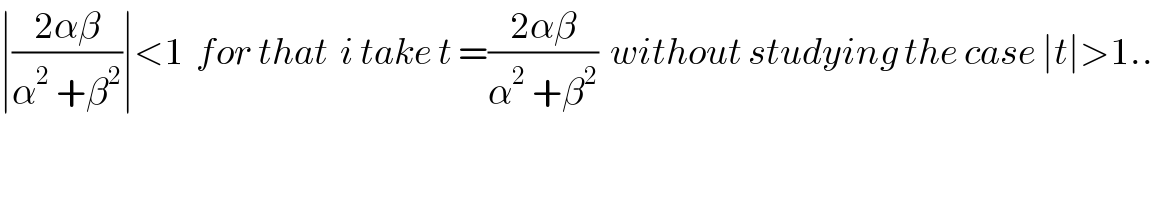
∣((2αβ)/(α^2 +β^2 ))∣<1 for that i take t =((2αβ)/(α^2 +β^2 )) without studying the case ∣t∣>1..
$$\mid\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\mid<\mathrm{1}\:\:{for}\:{that}\:\:{i}\:{take}\:{t}\:=\frac{\mathrm{2}\alpha\beta}{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\:\:{without}\:{studying}\:{the}\:{case}\:\mid{t}\mid>\mathrm{1}.. \\ $$
Commented by maxmathsup by imad last updated on 18/Jun/19
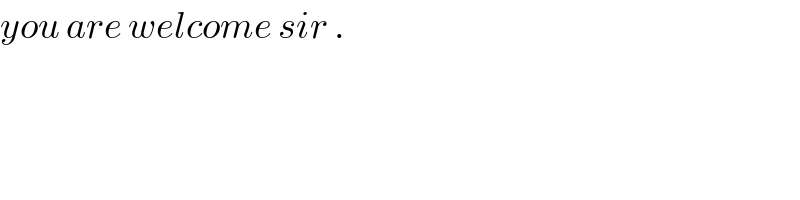
you are welcome sir .
$${you}\:{are}\:{welcome}\:{sir}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *