Question Number 62332 by tanmay last updated on 19/Jun/19
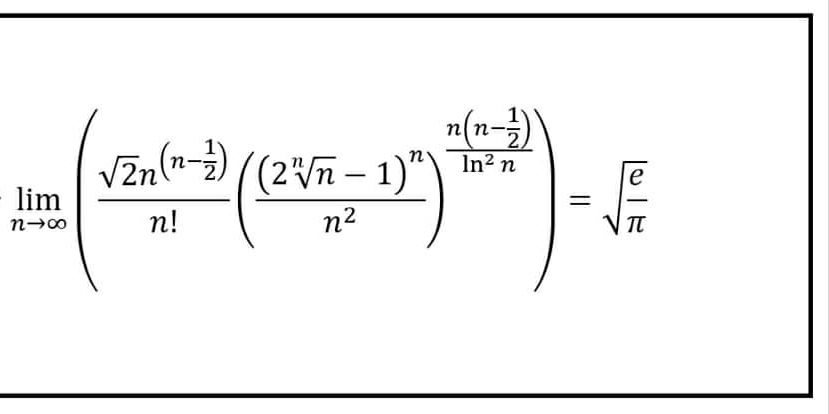
Answered by tanmay last updated on 20/Jun/19
![lim_(n→∞) [(((√2) ×n^(n−(1/2)) )/(n^(n+(1/2)) ×(√(2π)) ×e^(−n) ))×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] now =(1/( (√π)))lim_(n→∞) [(e^n /n)×{(((2n^(1/n) −1)^n^2 )/n^(2n) )}^((n−(1/2))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×{((n^n (2−(1/n^(1/n) ))^n^2 )/(n^n ×n^n ))}^((n−(1/2))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×{((2^n^2 (1−(1/(2n^(1/n) )))^n^2 )/n^n )}^((n−(1/2))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×(1−(1/(2n^(1/n) )))^(2n^(1/n) ×(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×e^(−(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/( (√π)))lim_(n→∞) [(e^n /n)×2^(n^2 ×((n−(1/2))/(ln^2 n))) ×(1/n^((n−(1/2))/(ln^2 n)) )×(e^((−1)/2) )^((n^2 /n^(1/n) )×((n−(1/2))/(ln^2 n))) ] (1/( (√π)))lim_(n→∞) wait](https://www.tinkutara.com/question/Q62359.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\sqrt{\mathrm{2}}\:×{n}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{{n}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ×\sqrt{\mathrm{2}\pi}\:×{e}^{−{n}} }×\left\{\frac{\left(\mathrm{2}×{n}^{\frac{\mathrm{1}}{{n}}} −\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\right\}^{\frac{{n}\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{\left(\mathrm{2}×{n}^{\frac{\mathrm{1}}{{n}}} −\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\right\}^{\frac{{n}\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$${now}\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{\left(\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} −\mathrm{1}\right)^{{n}^{\mathrm{2}} } }{{n}^{\mathrm{2}{n}} }\right\}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{{n}^{{n}} \left(\mathrm{2}−\frac{\mathrm{1}}{{n}^{\frac{\mathrm{1}}{{n}}} }\right)^{{n}^{\mathrm{2}} } }{{n}^{{n}} ×{n}^{{n}} }\right\}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{\mathrm{2}^{{n}^{\mathrm{2}} } \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} }\right)^{{n}^{\mathrm{2}} } }{{n}^{{n}} }\right\}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{\mathrm{2}^{{n}^{\mathrm{2}} } }{{n}^{{n}} }×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} }\right)^{\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} ×\frac{{n}^{\mathrm{2}} }{\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} }} \right\}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\left\{\frac{\mathrm{2}^{{n}^{\mathrm{2}} } }{{n}^{{n}} }×{e}^{−\frac{{n}^{\mathrm{2}} }{\mathrm{2}{n}^{\frac{\mathrm{1}}{{n}}} }} \right\}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{e}^{{n}} }{{n}}×\mathrm{2}^{{n}^{\mathrm{2}} ×\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} ×\frac{\mathrm{1}}{{n}^{\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} }×\left({e}^{\frac{−\mathrm{1}}{\mathrm{2}}} \right)^{\frac{{n}^{\mathrm{2}} }{{n}^{\frac{\mathrm{1}}{{n}}} }×\frac{{n}−\frac{\mathrm{1}}{\mathrm{2}}}{{ln}^{\mathrm{2}} {n}}} \right] \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{n}\rightarrow\infty} {\mathrm{li}{m}}\:\:\boldsymbol{{wait}} \\ $$
