Menu Close

Question-62347

Tinku Tara 0 Comments
Pin




Question Number 62347 by rajesh4661kumar@gamil.com last updated on 20/Jun/19
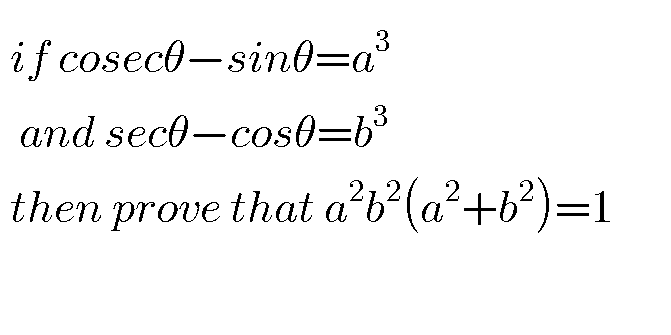
Answered by Kunal12588 last updated on 20/Jun/19
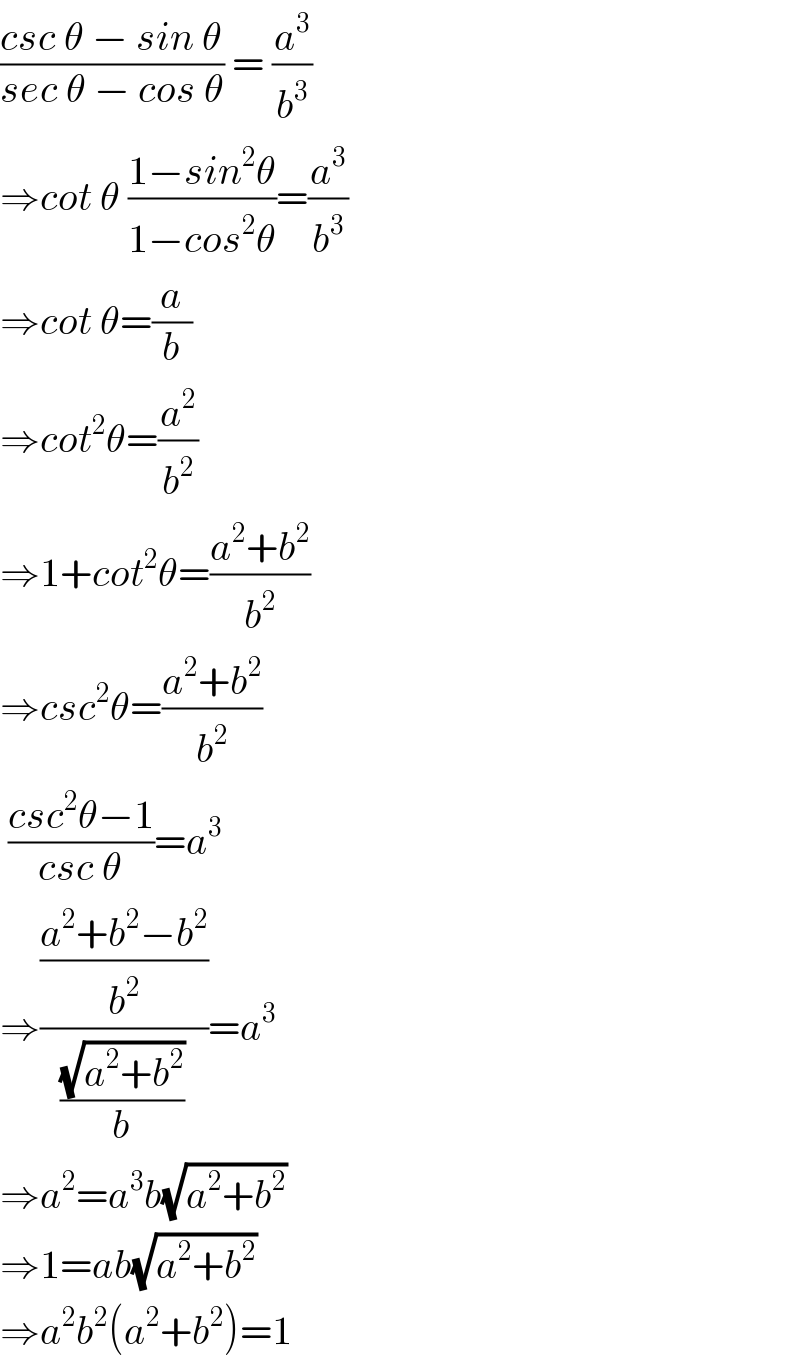
((csc θ − sin θ)/(sec θ − cos θ)) = (a^3 /b^3 ) ⇒cot θ ((1−sin^2 θ)/(1−cos^2 θ))=(a^3 /b^3 ) ⇒cot θ=(a/b) ⇒cot^2 θ=(a^2 /b^2 ) ⇒1+cot^2 θ=((a^2 +b^2 )/b^2 ) ⇒csc^2 θ=((a^2 +b^2 )/b^2 ) ((csc^2 θ−1)/(csc θ))=a^3 ⇒(((a^2 +b^2 −b^2 )/b^2 )/((√(a^2 +b^2 ))/b))=a^3 ⇒a^2 =a^3 b(√(a^2 +b^2 )) ⇒1=ab(√(a^2 +b^2 )) ⇒a^2 b^2 (a^2 +b^2 )=1
$$\frac{{csc}\:\theta\:−\:{sin}\:\theta}{{sec}\:\theta\:−\:{cos}\:\theta}\:=\:\frac{{a}^{\mathrm{3}} }{{b}^{\mathrm{3}} } \\ $$$$\Rightarrow{cot}\:\theta\:\frac{\mathrm{1}−{sin}^{\mathrm{2}} \theta}{\mathrm{1}−{cos}^{\mathrm{2}} \theta}=\frac{{a}^{\mathrm{3}} }{{b}^{\mathrm{3}} } \\ $$$$\Rightarrow{cot}\:\theta=\frac{{a}}{{b}} \\ $$$$\Rightarrow{cot}^{\mathrm{2}} \theta=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}+{cot}^{\mathrm{2}} \theta=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{csc}^{\mathrm{2}} \theta=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\:\frac{{csc}^{\mathrm{2}} \theta−\mathrm{1}}{{csc}\:\theta}={a}^{\mathrm{3}} \\ $$$$\Rightarrow\frac{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}}={a}^{\mathrm{3}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} ={a}^{\mathrm{3}} {b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}={ab}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\mathrm{1} \\ $$
Commented by peter frank last updated on 20/Jun/19
nice
$${nice} \\ $$
Answered by Kunal12588 last updated on 20/Jun/19
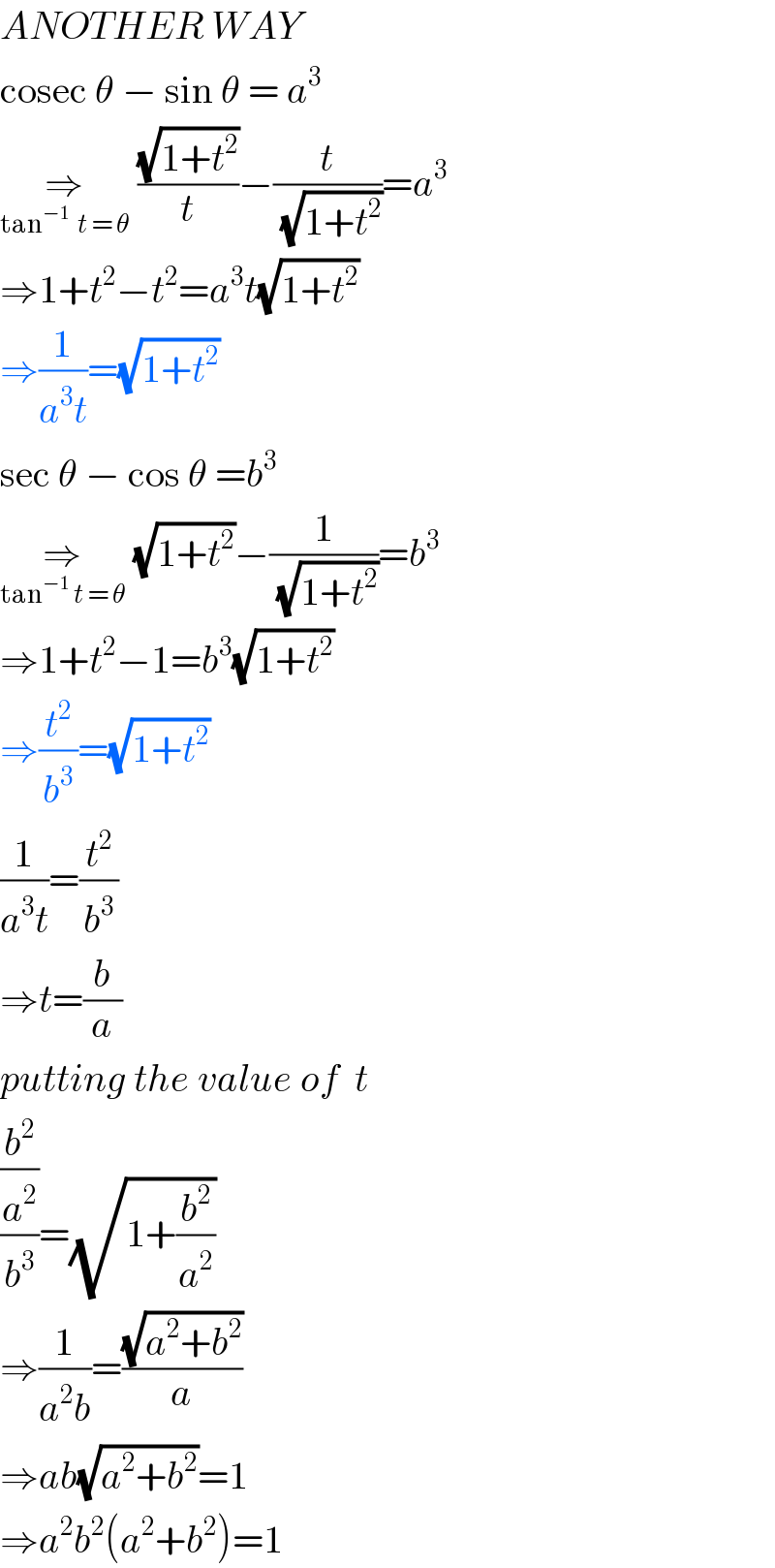
ANOTHER WAY cosec θ − sin θ = a^3 ⇒_(tan^(−1) t = θ) ((√(1+t^2 ))/t)−(t/( (√(1+t^2 ))))=a^3 ⇒1+t^2 −t^2 =a^3 t(√(1+t^2 )) ⇒(1/(a^3 t))=(√(1+t^2 )) sec θ − cos θ =b^3 ⇒_(tan^(−1) t = θ) (√(1+t^2 ))−(1/( (√(1+t^2 ))))=b^3 ⇒1+t^2 −1=b^3 (√(1+t^2 )) ⇒(t^2 /b^3 )=(√(1+t^2 )) (1/(a^3 t))=(t^2 /b^3 ) ⇒t=(b/a) putting the value of t ((b^2 /a^2 )/b^3 )=(√(1+(b^2 /a^2 ))) ⇒(1/(a^2 b))=((√(a^2 +b^2 ))/a) ⇒ab(√(a^2 +b^2 ))=1 ⇒a^2 b^2 (a^2 +b^2 )=1
$${ANOTHER}\:{WAY} \\ $$$$\mathrm{cosec}\:\theta\:−\:\mathrm{sin}\:\theta\:=\:{a}^{\mathrm{3}} \\ $$$$\underset{\mathrm{tan}^{−\mathrm{1}} \:\:{t}\:=\:\theta} {\Rightarrow}\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{{t}}−\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}={a}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{1}+{t}^{\mathrm{2}} −{t}^{\mathrm{2}} ={a}^{\mathrm{3}} {t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}^{\mathrm{3}} {t}}=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{sec}\:\theta\:−\:\mathrm{cos}\:\theta\:={b}^{\mathrm{3}} \\ $$$$\underset{\mathrm{tan}^{−\mathrm{1}} \:{t}\:=\:\theta} {\Rightarrow}\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}={b}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}={b}^{\mathrm{3}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{t}^{\mathrm{2}} }{{b}^{\mathrm{3}} }=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} {t}}=\frac{{t}^{\mathrm{2}} }{{b}^{\mathrm{3}} } \\ $$$$\Rightarrow{t}=\frac{{b}}{{a}} \\ $$$${putting}\:{the}\:{value}\:{of}\:\:{t} \\ $$$$\frac{\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{{b}^{\mathrm{3}} }=\sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{a}} \\ $$$$\Rightarrow{ab}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *