Question Number 62431 by rajesh4661kumar@gamil.com last updated on 21/Jun/19

Answered by tanmay last updated on 21/Jun/19
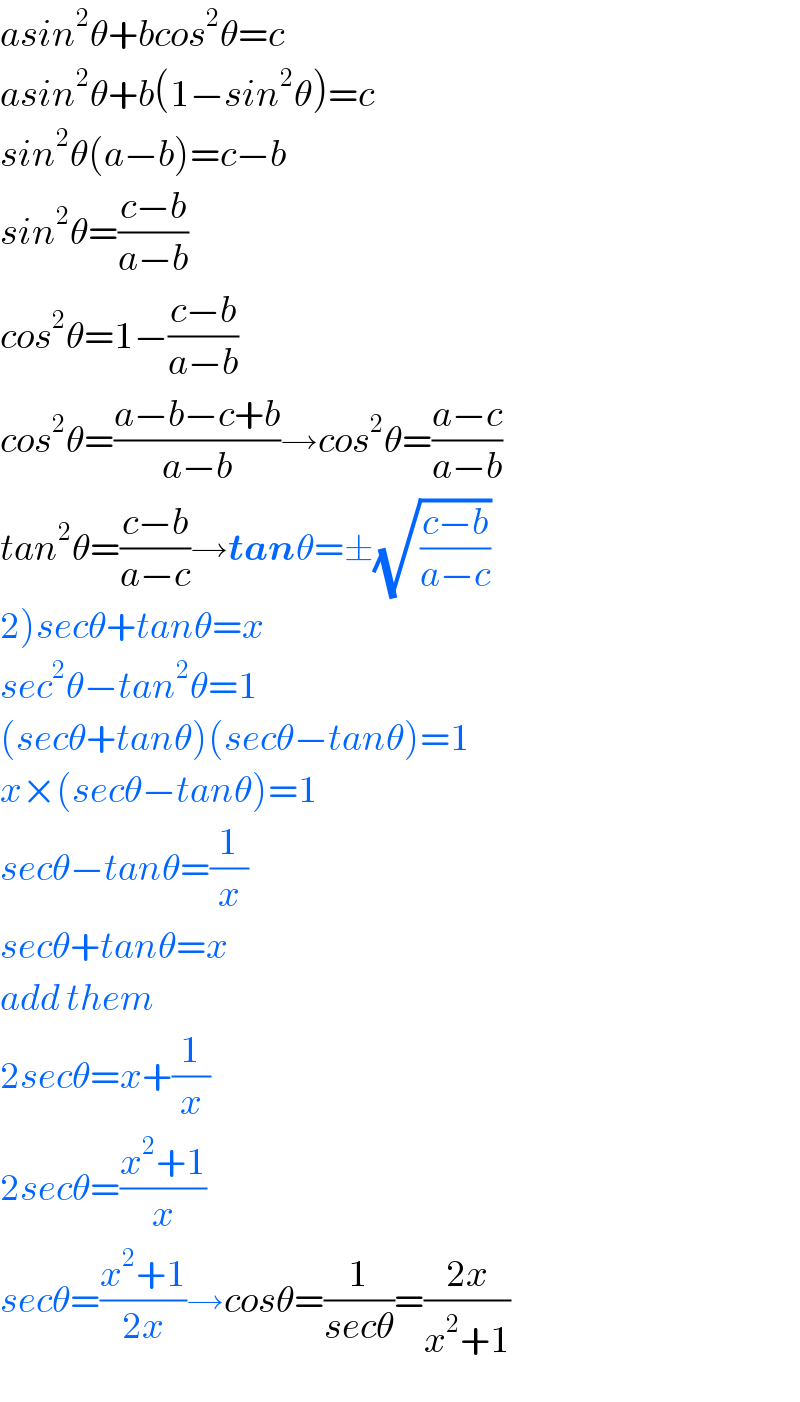
$${asin}^{\mathrm{2}} \theta+{bcos}^{\mathrm{2}} \theta={c} \\ $$$${asin}^{\mathrm{2}} \theta+{b}\left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right)={c} \\ $$$${sin}^{\mathrm{2}} \theta\left({a}−{b}\right)={c}−{b} \\ $$$${sin}^{\mathrm{2}} \theta=\frac{{c}−{b}}{{a}−{b}} \\ $$$${cos}^{\mathrm{2}} \theta=\mathrm{1}−\frac{{c}−{b}}{{a}−{b}} \\ $$$${cos}^{\mathrm{2}} \theta=\frac{{a}−{b}−{c}+{b}}{{a}−{b}}\rightarrow{cos}^{\mathrm{2}} \theta=\frac{{a}−{c}}{{a}−{b}} \\ $$$${tan}^{\mathrm{2}} \theta=\frac{{c}−{b}}{{a}−{c}}\rightarrow\boldsymbol{{tan}}\theta=\pm\sqrt{\frac{{c}−{b}}{{a}−{c}}}\: \\ $$$$\left.\mathrm{2}\right){sec}\theta+{tan}\theta={x} \\ $$$${sec}^{\mathrm{2}} \theta−{tan}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\left({sec}\theta+{tan}\theta\right)\left({sec}\theta−{tan}\theta\right)=\mathrm{1} \\ $$$${x}×\left({sec}\theta−{tan}\theta\right)=\mathrm{1} \\ $$$${sec}\theta−{tan}\theta=\frac{\mathrm{1}}{{x}} \\ $$$${sec}\theta+{tan}\theta={x} \\ $$$${add}\:{them} \\ $$$$\mathrm{2}{sec}\theta={x}+\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{2}{sec}\theta=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}} \\ $$$${sec}\theta=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}}\rightarrow{cos}\theta=\frac{\mathrm{1}}{{sec}\theta}=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by peter frank last updated on 22/Jun/19
$${thank}\:{you}\:{for}\:{wonder}\:{solution} \\ $$
