Menu Close

Question-62448

Tinku Tara 0 Comments
Pin




Question Number 62448 by mr W last updated on 21/Jun/19
Commented by mr W last updated on 21/Jun/19
The distances of a point M to the vertexes of a triangle are p,q,r. (assume p≥q≥r) Find the side lengthes and thus the area of the triangle with the largest area.
$${The}\:{distances}\:{of}\:{a}\:{point}\:{M}\:{to}\:{the} \\ $$$${vertexes}\:{of}\:{a}\:{triangle}\:{are}\:{p},{q},{r}. \\ $$$$\left({assume}\:{p}\geqslant{q}\geqslant{r}\right) \\ $$$${Find}\:{the}\:{side}\:{lengthes}\:{and}\:{thus}\:{the} \\ $$$${area}\:{of}\:{the}\:{triangle}\:{with}\:{the}\:{largest} \\ $$$${area}. \\ $$
Answered by ajfour last updated on 21/Jun/19
Commented by mr W last updated on 21/Jun/19
thanks for the wonderful solution sir! what′s the sense to calculate f ′(x)? as you proved, AM⊥BC, that′s also obviours for the maximum triangle, similarly BM⊥CA and CM⊥AB, i think we have the same case as in Q61861, i.e. point M should be the orthocenter of the triangle (but the one inside the triangle).
$${thanks}\:{for}\:{the}\:{wonderful}\:{solution}\:{sir}! \\ $$$${what}'{s}\:{the}\:{sense}\:{to}\:{calculate}\:{f}\:'\left({x}\right)? \\ $$$$ \\ $$$${as}\:{you}\:{proved},\:{AM}\bot{BC},\:{that}'{s}\:{also} \\ $$$${obviours}\:{for}\:{the}\:{maximum}\:{triangle}, \\ $$$${similarly}\:{BM}\bot{CA}\:{and}\:{CM}\bot{AB}, \\ $$$${i}\:{think}\:{we}\:{have}\:{the}\:{same}\:{case}\:{as}\:{in} \\ $$$${Q}\mathrm{61861},\:{i}.{e}.\:{point}\:{M}\:{should}\:{be}\:{the} \\ $$$${orthocenter}\:{of}\:{the}\:{triangle}\:\left({but}\:{the}\right. \\ $$$$\left.{one}\:{inside}\:{the}\:{triangle}\right). \\ $$
Commented by ajfour last updated on 21/Jun/19
2△=p(qsin θ+rsin φ)+qrsin (θ+φ) 2((∂△/∂θ))=pqcos θ+qrcos (θ+φ)=0 2((∂△/∂φ))=prcos φ+qrcos (θ+φ)=0 ⇒ qcos θ=rcos φ = x (say) > 0 ⇒ BC ⊥ AM px=−qrcos (θ+φ) ⇒ px=−x^2 +(√((q^2 −x^2 )(r^2 −x^2 ))) ⇒ x^2 (p+x)^2 =x^4 −(q^2 +r^2 )x^2 +q^2 r^2 ⇒ 2px^3 +(p^2 +q^2 +r^2 )x^2 −q^2 r^2 =0 let f(x)=2px^3 +(p^2 +q^2 +r^2 )x^2 −q^2 r^2 f ′(x)=2x(3px+p^2 +q^2 +r^2 ) ⇒ f(x) has only one +ve root, say x_0 . cos θ_0 =(x_0 /q) , cos φ_0 =(x_0 /r) △=(1/2){p(qsin θ_0 +rsin φ_0 )+qrsin (θ_0 +φ_0 )}
$$\mathrm{2}\bigtriangleup={p}\left({q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi\right)+{qr}\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\mathrm{2}\left(\frac{\partial\bigtriangleup}{\partial\theta}\right)={pq}\mathrm{cos}\:\theta+{qr}\mathrm{cos}\:\left(\theta+\phi\right)=\mathrm{0} \\ $$$$\mathrm{2}\left(\frac{\partial\bigtriangleup}{\partial\phi}\right)={pr}\mathrm{cos}\:\phi+{qr}\mathrm{cos}\:\left(\theta+\phi\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{q}\mathrm{cos}\:\theta={r}\mathrm{cos}\:\phi\:=\:{x}\:\left({say}\right)\:>\:\mathrm{0} \\ $$$$\Rightarrow\:{BC}\:\bot\:{AM} \\ $$$$\:\:\:\:{px}=−{qr}\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$$\Rightarrow\:\:{px}=−{x}^{\mathrm{2}} +\sqrt{\left({q}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} \left({p}+{x}\right)^{\mathrm{2}} ={x}^{\mathrm{4}} −\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){x}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}{px}^{\mathrm{3}} +\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){x}^{\mathrm{2}} −{q}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:{f}\left({x}\right)=\mathrm{2}{px}^{\mathrm{3}} +\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){x}^{\mathrm{2}} −{q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)=\mathrm{2}{x}\left(\mathrm{3}{px}+{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{f}\left({x}\right)\:{has}\:{only}\:{one}\:+{ve}\:{root}, \\ $$$${say}\:{x}_{\mathrm{0}} . \\ $$$$\:\:\:\mathrm{cos}\:\theta_{\mathrm{0}} =\frac{{x}_{\mathrm{0}} }{{q}}\:,\:\:\mathrm{cos}\:\phi_{\mathrm{0}} =\frac{{x}_{\mathrm{0}} }{{r}} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\left\{{p}\left({q}\mathrm{sin}\:\theta_{\mathrm{0}} +{r}\mathrm{sin}\:\phi_{\mathrm{0}} \right)+{qr}\mathrm{sin}\:\left(\theta_{\mathrm{0}} +\phi_{\mathrm{0}} \right)\right\} \\ $$$$ \\ $$
Commented by ajfour last updated on 21/Jun/19
f ′(x)=0 for x_1 =0 and x_2 < 0 while f(0)<0 , hence only one +ve root. [for this reason i find f ′(x)].
$${f}\:'\left({x}\right)=\mathrm{0}\:{for}\:\:{x}_{\mathrm{1}} =\mathrm{0}\:\:{and}\:{x}_{\mathrm{2}} \:<\:\mathrm{0} \\ $$$${while}\:{f}\left(\mathrm{0}\right)<\mathrm{0}\:,\:{hence}\:{only}\:{one} \\ $$$$+{ve}\:{root}.\:\left[{for}\:{this}\:{reason}\:{i}\:{find}\:{f}\:'\left({x}\right)\right]. \\ $$
Commented by mr W last updated on 21/Jun/19
2px^3 +(p^2 +q^2 +r^2 )x^2 −q^2 r^2 =0 ⇒x^3 +3((p^2 +q^2 +r^2 )/(6p))x^2 −2((q^2 r^2 )/(4p))=0 ⇒x^3 +3ux^2 −2v=0 x=u[2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+((2kπ)/3)}−1] λ=(x/p)=((p^2 +q^2 +r^2 )/(6p^2 ))[2 sin {(1/3) sin^(−1) (1−((54p^2 q^2 r^2 )/((p^2 +q^2 +r^2 )^3 )))+((2π)/3)}−1]
$$\mathrm{2}{px}^{\mathrm{3}} +\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){x}^{\mathrm{2}} −{q}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{3}} +\mathrm{3}\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{6}{p}}{x}^{\mathrm{2}} −\mathrm{2}\frac{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }{\mathrm{4}{p}}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{3}} +\mathrm{3}{ux}^{\mathrm{2}} −\mathrm{2}{v}=\mathrm{0} \\ $$$${x}={u}\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right] \\ $$$$\lambda=\frac{{x}}{{p}}=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{6}{p}^{\mathrm{2}} }\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{54}{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} }{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right] \\ $$
Commented by ajfour last updated on 21/Jun/19
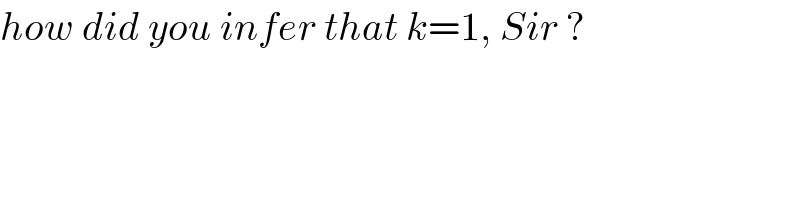
how did you infer that k=1, Sir ?
$${how}\:{did}\:{you}\:{infer}\:{that}\:{k}=\mathrm{1},\:{Sir}\:? \\ $$
Commented by mr W last updated on 21/Jun/19
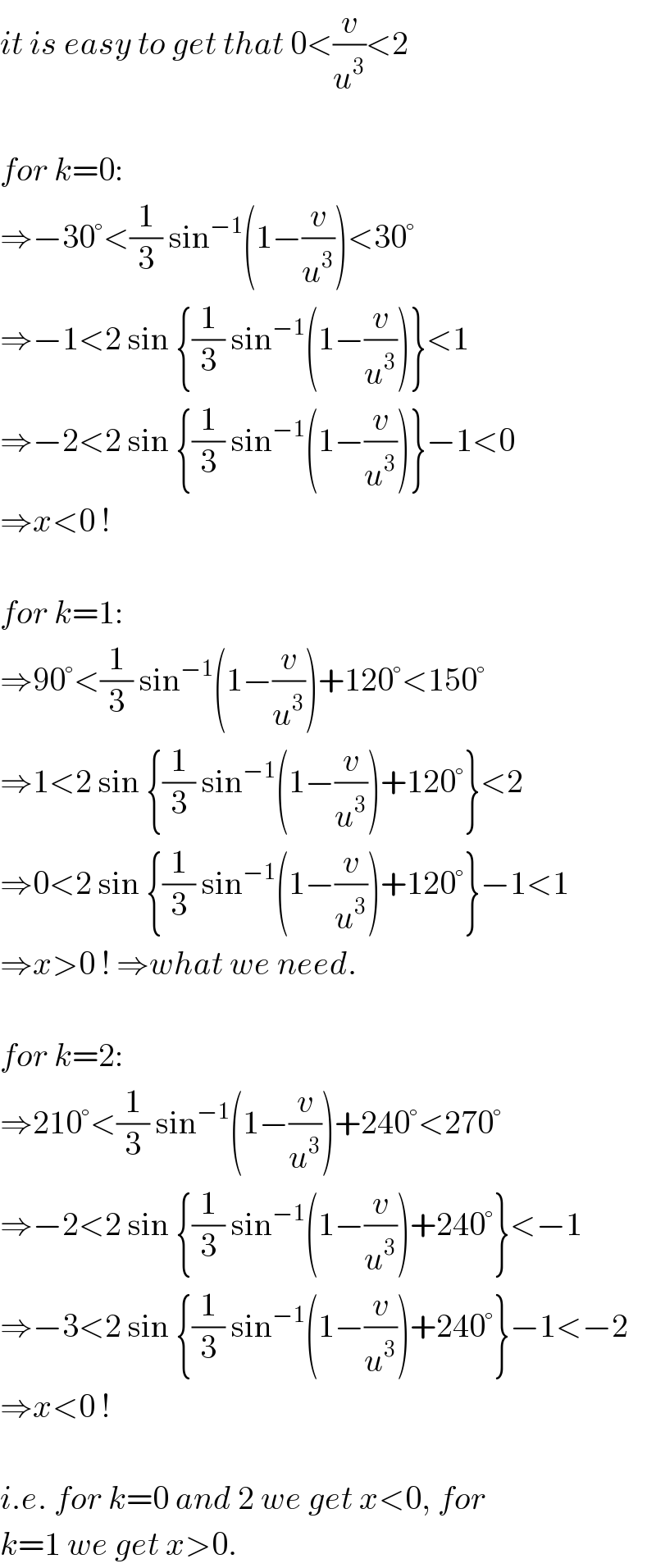
it is easy to get that 0<(v/u^3 )<2 for k=0: ⇒−30°<(1/3) sin^(−1) (1−(v/u^3 ))<30° ⇒−1<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))}<1 ⇒−2<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))}−1<0 ⇒x<0 ! for k=1: ⇒90°<(1/3) sin^(−1) (1−(v/u^3 ))+120°<150° ⇒1<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+120°}<2 ⇒0<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+120°}−1<1 ⇒x>0 ! ⇒what we need. for k=2: ⇒210°<(1/3) sin^(−1) (1−(v/u^3 ))+240°<270° ⇒−2<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+240°}<−1 ⇒−3<2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+240°}−1<−2 ⇒x<0 ! i.e. for k=0 and 2 we get x<0, for k=1 we get x>0.
$${it}\:{is}\:{easy}\:{to}\:{get}\:{that}\:\mathrm{0}<\frac{{v}}{{u}^{\mathrm{3}} }<\mathrm{2} \\ $$$$ \\ $$$${for}\:{k}=\mathrm{0}: \\ $$$$\Rightarrow−\mathrm{30}°<\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)<\mathrm{30}° \\ $$$$\Rightarrow−\mathrm{1}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)\right\}<\mathrm{1} \\ $$$$\Rightarrow−\mathrm{2}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)\right\}−\mathrm{1}<\mathrm{0} \\ $$$$\Rightarrow{x}<\mathrm{0}\:! \\ $$$$ \\ $$$${for}\:{k}=\mathrm{1}: \\ $$$$\Rightarrow\mathrm{90}°<\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{120}°<\mathrm{150}° \\ $$$$\Rightarrow\mathrm{1}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{120}°\right\}<\mathrm{2} \\ $$$$\Rightarrow\mathrm{0}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{120}°\right\}−\mathrm{1}<\mathrm{1} \\ $$$$\Rightarrow{x}>\mathrm{0}\:!\:\Rightarrow{what}\:{we}\:{need}. \\ $$$$ \\ $$$${for}\:{k}=\mathrm{2}: \\ $$$$\Rightarrow\mathrm{210}°<\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{240}°<\mathrm{270}° \\ $$$$\Rightarrow−\mathrm{2}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{240}°\right\}<−\mathrm{1} \\ $$$$\Rightarrow−\mathrm{3}<\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\mathrm{240}°\right\}−\mathrm{1}<−\mathrm{2} \\ $$$$\Rightarrow{x}<\mathrm{0}\:! \\ $$$$ \\ $$$${i}.{e}.\:{for}\:{k}=\mathrm{0}\:{and}\:\mathrm{2}\:{we}\:{get}\:{x}<\mathrm{0},\:{for} \\ $$$${k}=\mathrm{1}\:{we}\:{get}\:{x}>\mathrm{0}. \\ $$
Commented by mr W last updated on 22/Jun/19
your method yields the same result (for x) as in Q61861. λ=((p^2 +q^2 +r^2 )/(6p^2 ))[2 sin {(1/3) sin^(−1) (1−((54p^2 q^2 r^2 )/((p^2 +q^2 +r^2 )^3 )))+((2π)/3)}−1] a=(√(q^2 +λ^2 p^2 ))+(√(r^2 +λ^2 p^2 )) h=p(1+λ) Δ_(max) =((ah)/2)=(1/2)p^2 (1+λ)[(√(((q/p))^2 +λ^2 ))+(√(((r/p))^2 +λ^2 ))]
$${your}\:{method}\:{yields}\:{the}\:{same}\:{result}\:\left({for}\:{x}\right) \\ $$$${as}\:{in}\:{Q}\mathrm{61861}. \\ $$$$\lambda=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{6}{p}^{\mathrm{2}} }\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{54}{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} }{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right] \\ $$$${a}=\sqrt{{q}^{\mathrm{2}} +\lambda^{\mathrm{2}} {p}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} +\lambda^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$${h}={p}\left(\mathrm{1}+\lambda\right) \\ $$$$\Delta_{{max}} =\frac{{ah}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{p}^{\mathrm{2}} \left(\mathrm{1}+\lambda\right)\left[\sqrt{\left(\frac{{q}}{{p}}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} }+\sqrt{\left(\frac{{r}}{{p}}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} }\right] \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *