Question Number 62468 by bshahid010@gmail.com last updated on 21/Jun/19

Commented by mathmax by abdo last updated on 21/Jun/19
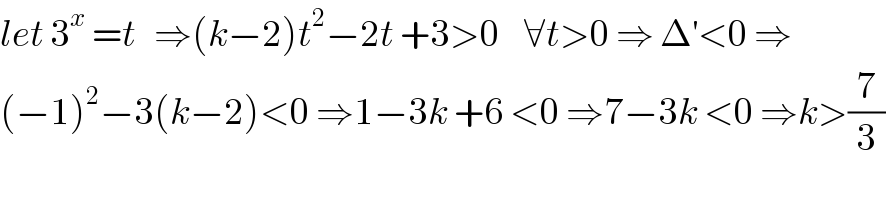
$${let}\:\mathrm{3}^{{x}} \:={t}\:\:\:\Rightarrow\left({k}−\mathrm{2}\right){t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{3}>\mathrm{0}\:\:\:\:\forall{t}>\mathrm{0}\:\Rightarrow\:\Delta^{'} <\mathrm{0}\:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left({k}−\mathrm{2}\right)<\mathrm{0}\:\Rightarrow\mathrm{1}−\mathrm{3}{k}\:+\mathrm{6}\:<\mathrm{0}\:\Rightarrow\mathrm{7}−\mathrm{3}{k}\:<\mathrm{0}\:\Rightarrow{k}>\frac{\mathrm{7}}{\mathrm{3}} \\ $$
Answered by mr W last updated on 21/Jun/19
![let t=3^x >0 (k−2)9^x −2∙3^x +3 =(k−2)t^2 −2t+3 =(k−2)[t^2 −((2t)/(k−2))+((1/(k−2)))^2 ]+3−(1/(k−2)) =(k−2)(t−(1/(k−2)))^2 +3−(1/(k−2)) such that it is always >0, we must have k−2>0 ∧3−(1/(k−2))>0 ⇒k>2 and ⇒3>(1/(k−2))⇒k−2>(1/3)⇒k>2+(1/3)=(7/3) ⇒answer is k>(7/3)](https://www.tinkutara.com/question/Q62475.png)
$${let}\:{t}=\mathrm{3}^{{x}} >\mathrm{0} \\ $$$$\left({k}−\mathrm{2}\right)\mathrm{9}^{{x}} −\mathrm{2}\centerdot\mathrm{3}^{{x}} +\mathrm{3} \\ $$$$=\left({k}−\mathrm{2}\right){t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3} \\ $$$$=\left({k}−\mathrm{2}\right)\left[{t}^{\mathrm{2}} −\frac{\mathrm{2}{t}}{{k}−\mathrm{2}}+\left(\frac{\mathrm{1}}{{k}−\mathrm{2}}\right)^{\mathrm{2}} \right]+\mathrm{3}−\frac{\mathrm{1}}{{k}−\mathrm{2}} \\ $$$$=\left({k}−\mathrm{2}\right)\left({t}−\frac{\mathrm{1}}{{k}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}−\frac{\mathrm{1}}{{k}−\mathrm{2}} \\ $$$${such}\:{that}\:{it}\:{is}\:{always}\:>\mathrm{0},\:{we}\:{must} \\ $$$${have}\:{k}−\mathrm{2}>\mathrm{0}\:\wedge\mathrm{3}−\frac{\mathrm{1}}{{k}−\mathrm{2}}>\mathrm{0} \\ $$$$\Rightarrow{k}>\mathrm{2}\:\:{and} \\ $$$$\Rightarrow\mathrm{3}>\frac{\mathrm{1}}{{k}−\mathrm{2}}\Rightarrow{k}−\mathrm{2}>\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{k}>\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\Rightarrow{answer}\:{is}\:{k}>\frac{\mathrm{7}}{\mathrm{3}} \\ $$
