Question Number 62486 by ajfour last updated on 21/Jun/19

Commented by ajfour last updated on 21/Jun/19

$${Find}\:{maximum}\:{perimeter}\:{of} \\ $$$${quadrilateral}\:{ABCD}. \\ $$
Answered by mr W last updated on 22/Jun/19
![p=(√(a^2 +b^2 −2ab cos θ))+(√(b^2 +c^2 −2bc cos ϕ))+(√(c^2 +d^2 −2cd cos φ))+(√(d^2 +a^2 −2da cos (2π−θ−ϕ−φ))) (∂p/∂θ)=((ab sin θ)/( (√(a^2 +b^2 −2ab cos θ))))−((da sin (2π−θ−ϕ−φ))/( (√(d^2 +a^2 −2da cos (2π−θ−ϕ−φ)))))=0 (∂p/∂ϕ)=((bc sin ϕ)/( (√(b^2 +c^2 −2bc cos ϕ))))−((da sin (2π−θ−ϕ−φ))/( (√(d^2 +a^2 −2da cos (2π−θ−ϕ−φ)))))=0 (∂p/∂φ)=((cd sin φ)/( (√(c^2 +d^2 −2cd cos φ))))−((da sin (2π−θ−ϕ−φ))/( (√(d^2 +a^2 −2da cos (2π−θ−ϕ−φ)))))=0 ((ab sin θ)/( (√(a^2 +b^2 −2ab cos θ))))=((da sin (2π−θ−ϕ−φ))/( (√(d^2 +a^2 −2da cos (2π−θ−ϕ−φ)))))=(√k) a^2 b^2 sin^2 θ=k(a^2 +b^2 −2ab cos θ) a^2 b^2 (1−cos^2 θ)=k(a^2 +b^2 −2ab cos θ) a^2 b^2 cos^2 θ−2abk cos θ+(a^2 +b^2 )k−a^2 b^2 =0 cos θ=((abk−(√(a^2 b^2 k^2 −a^2 b^2 [(a^2 +b^2 )k−a^2 b^2 ])))/(a^2 b^2 )) ⇒cos θ=((k−(√(k^2 −(a^2 +b^2 )k+a^2 b^2 )))/(ab)) ⇒θ=cos^(−1) ((k−(√(k^2 −(a^2 +b^2 )k+a^2 b^2 )))/(ab)) ⇒ϕ=cos^(−1) ((k−(√(k^2 −(b^2 +c^2 )k+b^2 c^2 )))/(bc)) ⇒φ=cos^(−1) ((k−(√(k^2 −(c^2 +d^2 )k+c^2 d^2 )))/(cd)) ⇒2π−(θ+ϕ+φ)=cos^(−1) ((k−(√(k^2 −(d^2 +a^2 )k+d^2 a^2 )))/da) we get k... example: a=10, b=8, c=6, d=5 ⇒k=21.2423 ⇒θ=117.3773° ⇒ϕ=94.6335° ⇒φ=62.6226°](https://www.tinkutara.com/question/Q62506.png)
$${p}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta}+\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\varphi}+\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\:\mathrm{cos}\:\phi}+\sqrt{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{da}\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)} \\ $$$$\frac{\partial{p}}{\partial\theta}=\frac{{ab}\:\mathrm{sin}\:\theta}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta}}−\frac{{da}\:\mathrm{sin}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}{\:\sqrt{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{da}\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}}=\mathrm{0} \\ $$$$\frac{\partial{p}}{\partial\varphi}=\frac{{bc}\:\mathrm{sin}\:\varphi}{\:\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\varphi}}−\frac{{da}\:\mathrm{sin}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}{\:\sqrt{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{da}\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}}=\mathrm{0} \\ $$$$\frac{\partial{p}}{\partial\phi}=\frac{{cd}\:\mathrm{sin}\:\phi}{\:\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\:\mathrm{cos}\:\phi}}−\frac{{da}\:\mathrm{sin}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}{\:\sqrt{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{da}\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}}=\mathrm{0} \\ $$$$\frac{{ab}\:\mathrm{sin}\:\theta}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta}}=\frac{{da}\:\mathrm{sin}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}{\:\sqrt{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{da}\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta−\varphi−\phi\right)}}=\sqrt{{k}} \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta={k}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta\right) \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)={k}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta\right) \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}{abk}\:\mathrm{cos}\:\theta+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){k}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{cos}\:\theta=\frac{{abk}−\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {k}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){k}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right]}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){k}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}{{ab}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){k}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}{{ab}} \\ $$$$\Rightarrow\varphi=\mathrm{cos}^{−\mathrm{1}} \frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){k}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} }}{{bc}} \\ $$$$\Rightarrow\phi=\mathrm{cos}^{−\mathrm{1}} \frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){k}+{c}^{\mathrm{2}} {d}^{\mathrm{2}} }}{{cd}} \\ $$$$\Rightarrow\mathrm{2}\pi−\left(\theta+\varphi+\phi\right)=\mathrm{cos}^{−\mathrm{1}} \frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({d}^{\mathrm{2}} +{a}^{\mathrm{2}} \right){k}+{d}^{\mathrm{2}} {a}^{\mathrm{2}} }}{{da}} \\ $$$${we}\:{get}\:{k}… \\ $$$${example}:\:{a}=\mathrm{10},\:{b}=\mathrm{8},\:{c}=\mathrm{6},\:{d}=\mathrm{5} \\ $$$$\Rightarrow{k}=\mathrm{21}.\mathrm{2423} \\ $$$$\Rightarrow\theta=\mathrm{117}.\mathrm{3773}° \\ $$$$\Rightarrow\varphi=\mathrm{94}.\mathrm{6335}° \\ $$$$\Rightarrow\phi=\mathrm{62}.\mathrm{6226}° \\ $$
Commented by peter frank last updated on 22/Jun/19
$${congratulation}\:{sir}\:{for}\:{hard}\:{work}\: \\ $$
Commented by ajfour last updated on 22/Jun/19
$${Thanks}\:{Sir},\:{but}\:{i}\:{wished},\:{we}\:{could} \\ $$$${crack}\:{it}\:{by}\:{some}\:{geometrical}\:{way}? \\ $$$${Thank}\:{you}\:{anyway}. \\ $$
Answered by mr W last updated on 23/Jun/19
![O should be the incircle center such that the quadrilateral has maximum perimeter (see Q62542) let r=radius of the incircle ∠A=2 sin^(−1) (r/a) ∠B=2 sin^(−1) (r/b) ∠C=2 sin^(−1) (r/c) ∠D=2 sin^(−1) (r/d) ∠A+∠B+∠C+∠D=2π sin^(−1) (r/a)+sin^(−1) (r/b)+sin^(−1) (r/c)+sin^(−1) (r/d)=π cos (sin^(−1) (r/a)+sin^(−1) (r/b))=cos (π−sin^(−1) (r/c)−sin^(−1) (r/d)) (√((1−(r^2 /a^2 ))(1−(r^2 /b^2 ))))−(r^2 /(ab))=−(√((1−(r^2 /c^2 ))(1−(r^2 /d^2 ))))+(r^2 /(cd)) (√((1−(r^2 /a^2 ))(1−(r^2 /b^2 ))))−(√((1−(r^2 /c^2 ))(1−(r^2 /d^2 ))))=(r^2 /(ab))+(r^2 /(cd)) (1−(r^2 /a^2 ))(1−(r^2 /b^2 ))+(1−(r^2 /c^2 ))(1−(r^2 /d^2 ))−2(√((1−(r^2 /a^2 ))(1−(r^2 /b^2 ))(1−(r^2 /c^2 ))(1−(r^2 /d^2 ))))=(r^4 /(a^2 b^2 ))+(r^4 /(c^2 d^2 ))+((2r^4 )/(abcd)) 2−((r^2 /a^2 )+(r^2 /b^2 )+(r^2 /c^2 )+(r^2 /d^2 ))+(r^4 /(a^2 b^2 ))+(r^4 /(c^2 d^2 ))−2(√((1−(r^2 /a^2 ))(1−(r^2 /b^2 ))(1−(r^2 /c^2 ))(1−(r^2 /d^2 ))))=(r^4 /(a^2 b^2 ))+(r^4 /(c^2 d^2 ))+((2r^4 )/(abcd)) (√((1−(r^2 /a^2 ))(1−(r^2 /b^2 ))(1−(r^2 /c^2 ))(1−(r^2 /d^2 ))))=1−(1/2)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^2 −(r^4 /(abcd)) [1−((r^2 /a^2 )+(r^2 /b^2 ))+(r^4 /(a^2 b^2 ))][1−((r^2 /c^2 )+(r^2 /d^2 ))+(r^4 /(c^2 d^2 ))]=1+(1/4)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))^2 r^4 +(r^8 /(a^2 b^2 c^2 d^2 ))−((2r^4 )/(abcd))−((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^2 +(1/(abcd))((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^6 1−((r^2 /a^2 )+(r^2 /b^2 ))+(r^4 /(a^2 b^2 ))−((r^2 /c^2 )+(r^2 /d^2 ))+((r^2 /a^2 )+(r^2 /b^2 ))((r^2 /c^2 )+(r^2 /d^2 ))−(r^4 /(a^2 b^2 ))((r^2 /c^2 )+(r^2 /d^2 ))+(r^4 /(c^2 d^2 ))−(r^4 /(c^2 d^2 ))((r^2 /a^2 )+(r^2 /b^2 ))+(r^8 /(a^2 b^2 c^2 d^2 ))=1+(1/4)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))^2 r^4 +(r^8 /(a^2 b^2 c^2 d^2 ))−((2r^4 )/(abcd))−((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^2 +(1/(abcd))((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^6 ((1/(a^2 b^2 ))+(1/(a^2 c^2 ))+(1/(a^2 d^2 ))+(1/(b^2 c^2 ))+(1/(b^2 d^2 ))+(1/(c^2 d^2 )))−(((a^2 +b^2 +c^2 +d^2 )/(a^2 b^2 c^2 d^2 )))r^2 =(1/4)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))^2 −(2/(abcd))+(1/(abcd))((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))r^2 ⇒[(1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 )+((a^2 +b^2 +c^2 +d^2 )/(abcd))]r^2 =2+(((cd)/(ab))+((ab)/(cd))+((bd)/(ac))+((bc)/(ad))+((ad)/(bc))+((ac)/(bd)))−((abcd)/4)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))^2 ⇒r=(√((2+(((cd)/(ab))+((ab)/(cd))+((bd)/(ac))+((bc)/(ad))+((ad)/(bc))+((ac)/(bd)))−((abcd)/4)((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 ))^2 )/((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 )+((a^2 +b^2 +c^2 +d^2 )/(abcd)))))](https://www.tinkutara.com/question/Q62586.png)
$${O}\:{should}\:{be}\:{the}\:{incircle}\:{center}\:{such} \\ $$$${that}\:{the}\:{quadrilateral}\:{has}\:{maximum} \\ $$$${perimeter}\:\left({see}\:{Q}\mathrm{62542}\right) \\ $$$${let}\:{r}={radius}\:{of}\:{the}\:{incircle} \\ $$$$\angle{A}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{a}} \\ $$$$\angle{B}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}} \\ $$$$\angle{C}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}} \\ $$$$\angle{D}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{d}} \\ $$$$\angle{A}+\angle{B}+\angle{C}+\angle{D}=\mathrm{2}\pi \\ $$$$\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{a}}+\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}}+\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}}+\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{d}}=\pi \\ $$$$\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{a}}+\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}}\right)=\mathrm{cos}\:\left(\pi−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}}−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{d}}\right) \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)}−\frac{{r}^{\mathrm{2}} }{{ab}}=−\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)}+\frac{{r}^{\mathrm{2}} }{{cd}} \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)}−\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)}=\frac{{r}^{\mathrm{2}} }{{ab}}+\frac{{r}^{\mathrm{2}} }{{cd}} \\ $$$$\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)+\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)−\mathrm{2}\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)}=\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }+\frac{\mathrm{2}{r}^{\mathrm{4}} }{{abcd}} \\ $$$$\mathrm{2}−\left(\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }−\mathrm{2}\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)}=\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }+\frac{\mathrm{2}{r}^{\mathrm{4}} }{{abcd}} \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{2}} −\frac{{r}^{\mathrm{4}} }{{abcd}} \\ $$$$\left[\mathrm{1}−\left(\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right]\left[\mathrm{1}−\left(\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }\right]=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} {r}^{\mathrm{4}} +\frac{{r}^{\mathrm{8}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} }−\frac{\mathrm{2}{r}^{\mathrm{4}} }{{abcd}}−\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{2}} +\frac{\mathrm{1}}{{abcd}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{6}} \\ $$$$\mathrm{1}−\left(\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }−\left(\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)+\left(\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)−\frac{{r}^{\mathrm{4}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\left(\frac{{r}^{\mathrm{2}} }{{c}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{d}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }−\frac{{r}^{\mathrm{4}} }{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }\left(\frac{{r}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)+\frac{{r}^{\mathrm{8}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} {r}^{\mathrm{4}} +\frac{{r}^{\mathrm{8}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} }−\frac{\mathrm{2}{r}^{\mathrm{4}} }{{abcd}}−\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{2}} +\frac{\mathrm{1}}{{abcd}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{6}} \\ $$$$\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{2}} {c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{2}} {d}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} {c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} {d}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} {d}^{\mathrm{2}} }\right)−\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} }\right){r}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} −\frac{\mathrm{2}}{{abcd}}+\frac{\mathrm{1}}{{abcd}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right){r}^{\mathrm{2}} \\ $$$$\Rightarrow\left[\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{{abcd}}\right]{r}^{\mathrm{2}} =\mathrm{2}+\left(\frac{{cd}}{{ab}}+\frac{{ab}}{{cd}}+\frac{{bd}}{{ac}}+\frac{{bc}}{{ad}}+\frac{{ad}}{{bc}}+\frac{{ac}}{{bd}}\right)−\frac{{abcd}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\sqrt{\frac{\mathrm{2}+\left(\frac{{cd}}{{ab}}+\frac{{ab}}{{cd}}+\frac{{bd}}{{ac}}+\frac{{bc}}{{ad}}+\frac{{ad}}{{bc}}+\frac{{ac}}{{bd}}\right)−\frac{{abcd}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{{abcd}}}} \\ $$
Commented by ajfour last updated on 24/Jun/19
$${Immensely}\:{Beautiful}\:{Sir}! \\ $$
Commented by mr W last updated on 23/Jun/19

$${thanks}\:{for}\:{checking}\:{sir}!\:{i}\:{had}\:{a}\:{mistake} \\ $$$${in}\:{the}\:{working},\:{now}\:{fixed}. \\ $$$${with}\:{a}={b}={c}={d}\:{we}'{ll}\:{get}\:{r}=\frac{{a}}{\:\sqrt{\mathrm{2}}}. \\ $$
Commented by mr W last updated on 23/Jun/19
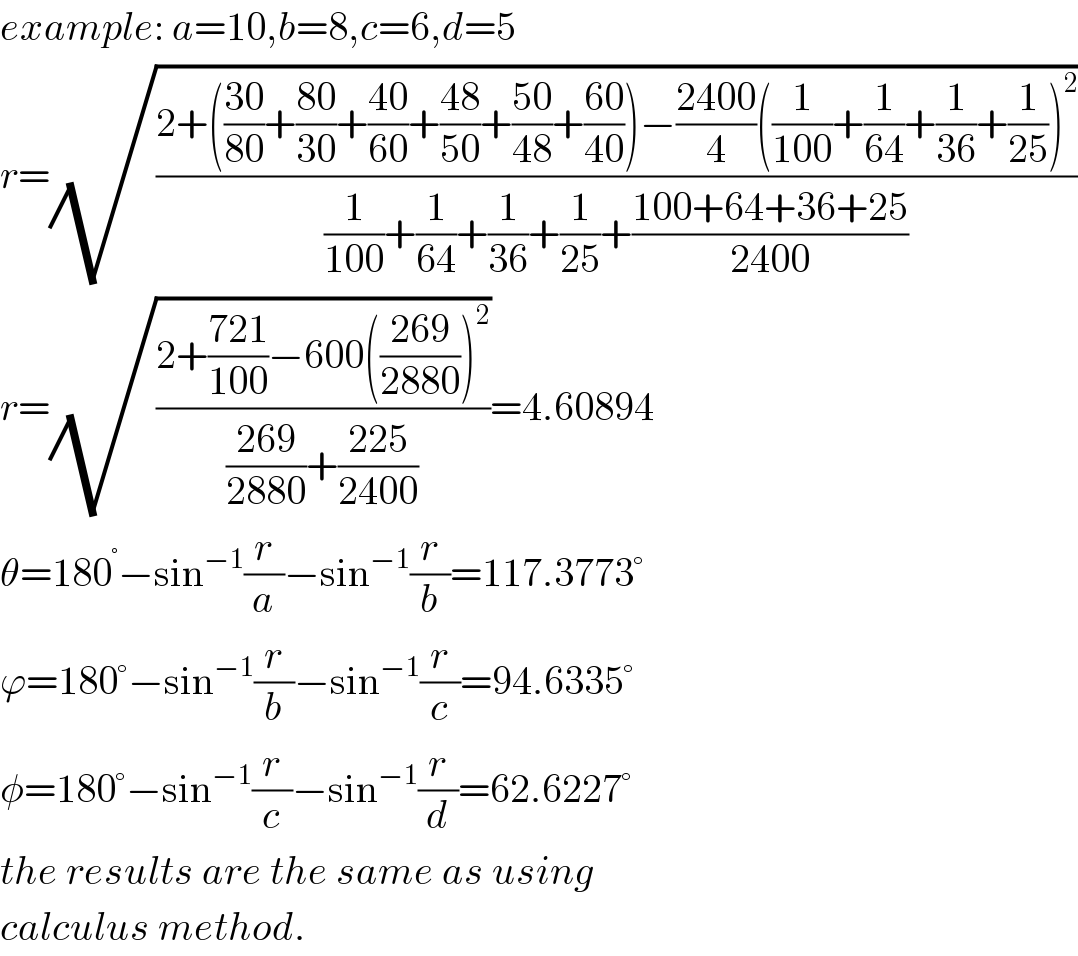
$${example}:\:{a}=\mathrm{10},{b}=\mathrm{8},{c}=\mathrm{6},{d}=\mathrm{5} \\ $$$${r}=\sqrt{\frac{\mathrm{2}+\left(\frac{\mathrm{30}}{\mathrm{80}}+\frac{\mathrm{80}}{\mathrm{30}}+\frac{\mathrm{40}}{\mathrm{60}}+\frac{\mathrm{48}}{\mathrm{50}}+\frac{\mathrm{50}}{\mathrm{48}}+\frac{\mathrm{60}}{\mathrm{40}}\right)−\frac{\mathrm{2400}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{100}}+\frac{\mathrm{1}}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{36}}+\frac{\mathrm{1}}{\mathrm{25}}\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{100}}+\frac{\mathrm{1}}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{36}}+\frac{\mathrm{1}}{\mathrm{25}}+\frac{\mathrm{100}+\mathrm{64}+\mathrm{36}+\mathrm{25}}{\mathrm{2400}}}} \\ $$$${r}=\sqrt{\frac{\mathrm{2}+\frac{\mathrm{721}}{\mathrm{100}}−\mathrm{600}\left(\frac{\mathrm{269}}{\mathrm{2880}}\right)^{\mathrm{2}} }{\frac{\mathrm{269}}{\mathrm{2880}}+\frac{\mathrm{225}}{\mathrm{2400}}}}=\mathrm{4}.\mathrm{60894} \\ $$$$\theta=\mathrm{180}^{°} −\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{a}}−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}}=\mathrm{117}.\mathrm{3773}° \\ $$$$\varphi=\mathrm{180}°−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{b}}−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}}=\mathrm{94}.\mathrm{6335}° \\ $$$$\phi=\mathrm{180}°−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{c}}−\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{d}}=\mathrm{62}.\mathrm{6227}° \\ $$$${the}\:{results}\:{are}\:{the}\:{same}\:{as}\:{using}\: \\ $$$${calculus}\:{method}. \\ $$
Commented by ajfour last updated on 24/Jun/19
$$\boldsymbol{\mathcal{I}}{ts}\:{a}\:\mathcal{D}{iscovery}\:{then}\:{Sir},\: \\ $$$$\boldsymbol{\mathcal{C}}{ongratulations},\:{and}\:{thanks} \\ $$$${for}\:{sharing}\:{it}. \\ $$
Commented by mr W last updated on 24/Jun/19

$${thanks}\:{sir}! \\ $$$${i}\:{didn}'{t}\:{expect}\:{that}\:{the}\:{solution}\:{for} \\ $$$${quadrilateral}\:{is}\:{even}\:{easier}\:{than}\:{for} \\ $$$${triangle}.\:{i}\:{mean}\:{without}\:{cubic}\:{equation}. \\ $$
