Question Number 62517 by Tawa1 last updated on 22/Jun/19

Commented by $@ty@m last updated on 22/Jun/19
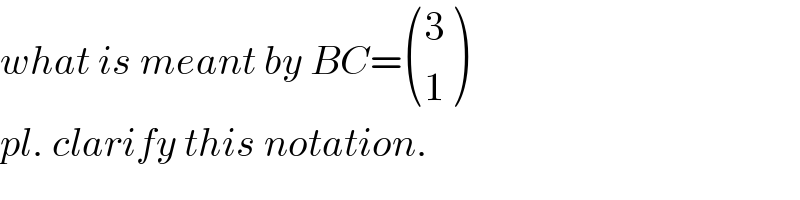
$${what}\:{is}\:{meant}\:{by}\:{BC}=\begin{pmatrix}{\mathrm{3}}\\{\mathrm{1}}\end{pmatrix}\: \\ $$$${pl}.\:{clarify}\:{this}\:{notation}. \\ $$
Commented by Prithwish sen last updated on 22/Jun/19

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\: \\ $$$$\mathrm{BC}\:=\:\mathrm{3}\hat {\boldsymbol{\mathrm{i}}}+\mathrm{1}\hat {\boldsymbol{\mathrm{j}}} \\ $$
Answered by tanmay last updated on 22/Jun/19
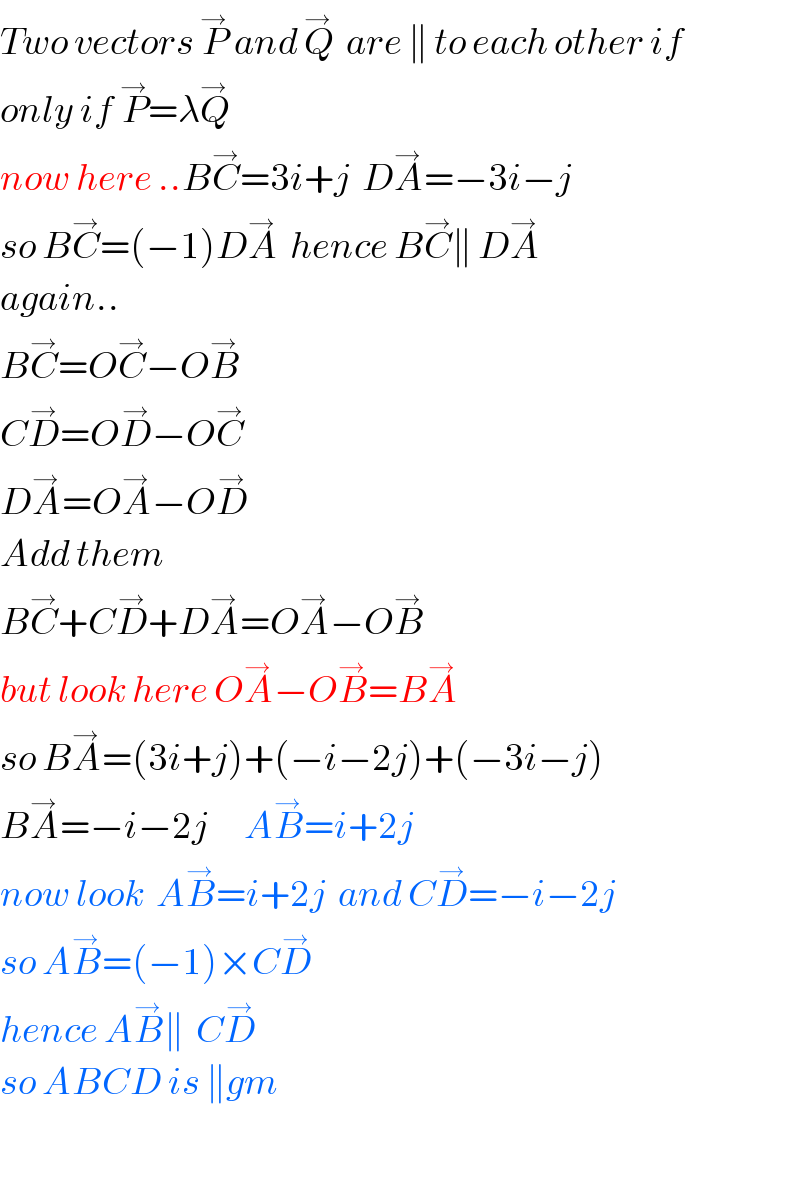
$${Two}\:{vectors}\:\overset{\rightarrow} {{P}}\:{and}\:\overset{\rightarrow} {{Q}}\:\:{are}\:\parallel\:{to}\:{each}\:{other}\:{if}\: \\ $$$${only}\:{if}\:\overset{\rightarrow} {{P}}=\lambda\overset{\rightarrow} {{Q}} \\ $$$${now}\:{here}\:..{B}\overset{\rightarrow} {{C}}=\mathrm{3}{i}+{j}\:\:{D}\overset{\rightarrow} {{A}}=−\mathrm{3}{i}−{j} \\ $$$${so}\:{B}\overset{\rightarrow} {{C}}=\left(−\mathrm{1}\right){D}\overset{\rightarrow} {{A}}\:\:{hence}\:{B}\overset{\rightarrow} {{C}}\parallel\:{D}\overset{\rightarrow} {{A}} \\ $$$${again}.. \\ $$$${B}\overset{\rightarrow} {{C}}={O}\overset{\rightarrow} {{C}}−{O}\overset{\rightarrow} {{B}} \\ $$$${C}\overset{\rightarrow} {{D}}={O}\overset{\rightarrow} {{D}}−{O}\overset{\rightarrow} {{C}} \\ $$$${D}\overset{\rightarrow} {{A}}={O}\overset{\rightarrow} {{A}}−{O}\overset{\rightarrow} {{D}} \\ $$$${Add}\:{them} \\ $$$${B}\overset{\rightarrow} {{C}}+{C}\overset{\rightarrow} {{D}}+{D}\overset{\rightarrow} {{A}}={O}\overset{\rightarrow} {{A}}−{O}\overset{\rightarrow} {{B}} \\ $$$${but}\:{look}\:{here}\:{O}\overset{\rightarrow} {{A}}−{O}\overset{\rightarrow} {{B}}={B}\overset{\rightarrow} {{A}} \\ $$$${so}\:{B}\overset{\rightarrow} {{A}}=\left(\mathrm{3}{i}+{j}\right)+\left(−{i}−\mathrm{2}{j}\right)+\left(−\mathrm{3}{i}−{j}\right) \\ $$$${B}\overset{\rightarrow} {{A}}=−{i}−\mathrm{2}{j}\:\:\:\:\:\:{A}\overset{\rightarrow} {{B}}={i}+\mathrm{2}{j} \\ $$$${now}\:{look}\:\:{A}\overset{\rightarrow} {{B}}={i}+\mathrm{2}{j}\:\:{and}\:{C}\overset{\rightarrow} {{D}}=−{i}−\mathrm{2}{j} \\ $$$${so}\:{A}\overset{\rightarrow} {{B}}=\left(−\mathrm{1}\right)×{C}\overset{\rightarrow} {{D}} \\ $$$${hence}\:{A}\overset{\rightarrow} {{B}}\parallel\:\:{C}\overset{\rightarrow} {{D}} \\ $$$${so}\:{ABCD}\:{is}\:\parallel{gm} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 22/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by $@ty@m last updated on 22/Jun/19

$$\because{B}\overset{\rightarrow} {{C}}=−{D}\overset{\rightarrow} {{A}} \\ $$$$\Rightarrow{BC}\parallel{AD}\:…\left({i}\right) \\ $$$${B}\overset{\rightarrow} {{A}}={B}\overset{\rightarrow} {{C}}+{C}\overset{\rightarrow} {{D}}+{D}\overset{\rightarrow} {{A}}=\begin{pmatrix}{−\mathrm{1}}\\{−\mathrm{2}}\end{pmatrix} \\ $$$$\therefore{B}\overset{\rightarrow} {{A}}={C}\overset{\rightarrow} {{D}} \\ $$$$\Rightarrow{BA}\parallel{CD}\:…\left({ii}\right) \\ $$$${From}\:\left({i}\right)\:\&\left({ii}\right),\:{we}\:{conclude}\:{that} \\ $$$${ABCD}\:{is}\:{a}\:{parallelogram}. \\ $$
Commented by Tawa1 last updated on 22/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 22/Jun/19
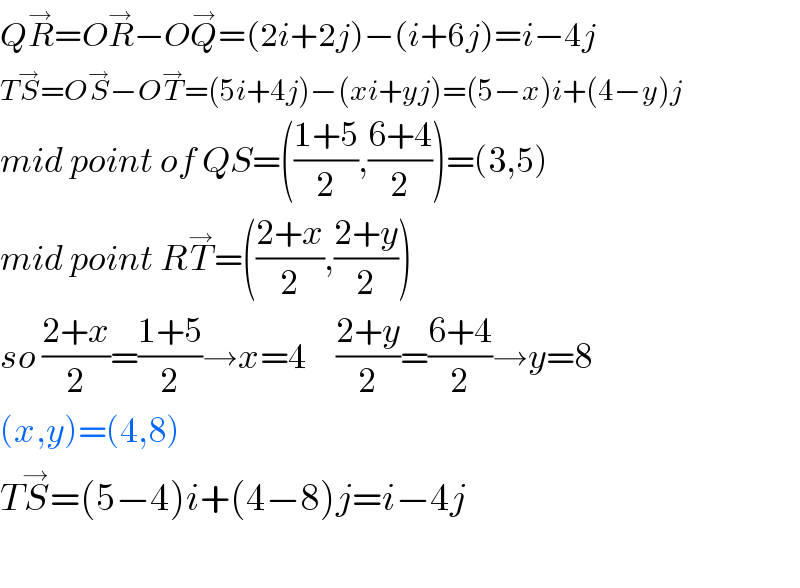
$${Q}\overset{\rightarrow} {{R}}={O}\overset{\rightarrow} {{R}}−{O}\overset{\rightarrow} {{Q}}=\left(\mathrm{2}{i}+\mathrm{2}{j}\right)−\left({i}+\mathrm{6}{j}\right)={i}−\mathrm{4}{j} \\ $$$${T}\overset{\rightarrow} {{S}}={O}\overset{\rightarrow} {{S}}−{O}\overset{\rightarrow} {{T}}=\left(\mathrm{5}{i}+\mathrm{4}{j}\right)−\left({xi}+{yj}\right)=\left(\mathrm{5}−{x}\right){i}+\left(\mathrm{4}−{y}\right){j} \\ $$$${mid}\:{point}\:{of}\:{QS}=\left(\frac{\mathrm{1}+\mathrm{5}}{\mathrm{2}},\frac{\mathrm{6}+\mathrm{4}}{\mathrm{2}}\right)=\left(\mathrm{3},\mathrm{5}\right) \\ $$$${mid}\:{point}\:{R}\overset{\rightarrow} {{T}}=\left(\frac{\mathrm{2}+{x}}{\mathrm{2}},\frac{\mathrm{2}+{y}}{\mathrm{2}}\right) \\ $$$${so}\:\frac{\mathrm{2}+{x}}{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{5}}{\mathrm{2}}\rightarrow{x}=\mathrm{4}\:\:\:\:\:\frac{\mathrm{2}+{y}}{\mathrm{2}}=\frac{\mathrm{6}+\mathrm{4}}{\mathrm{2}}\rightarrow{y}=\mathrm{8} \\ $$$$\left({x},{y}\right)=\left(\mathrm{4},\mathrm{8}\right) \\ $$$${T}\overset{\rightarrow} {{S}}=\left(\mathrm{5}−\mathrm{4}\right){i}+\left(\mathrm{4}−\mathrm{8}\right){j}={i}−\mathrm{4}{j} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 22/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 22/Jun/19
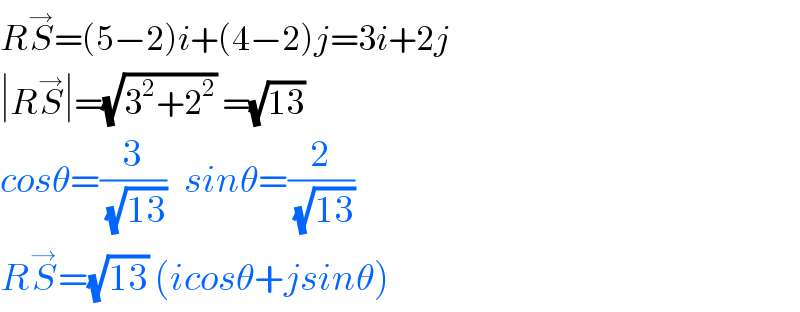
$${R}\overset{\rightarrow} {{S}}=\left(\mathrm{5}−\mathrm{2}\right){i}+\left(\mathrm{4}−\mathrm{2}\right){j}=\mathrm{3}{i}+\mathrm{2}{j} \\ $$$$\mid{R}\overset{\rightarrow} {{S}}\mid=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:=\sqrt{\mathrm{13}}\: \\ $$$${cos}\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}\:\:\:{sin}\theta=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}} \\ $$$${R}\overset{\rightarrow} {{S}}=\sqrt{\mathrm{13}}\:\left({icos}\theta+{jsin}\theta\right) \\ $$
Commented by Tawa1 last updated on 22/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
