Question Number 62570 by aliesam last updated on 23/Jun/19
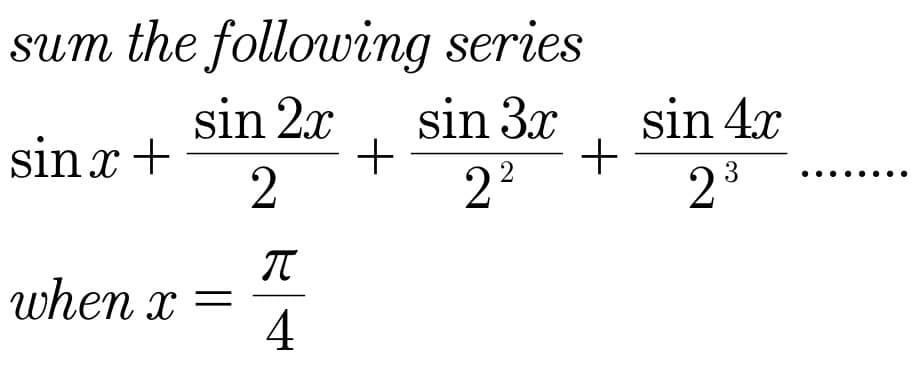
Commented by mathmax by abdo last updated on 23/Jun/19

$${we}\:{have}\:{S}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{\mathrm{2}^{{n}−\mathrm{1}} }\:=\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{\mathrm{2}^{{n}} }\:=\mathrm{2}\:{Im}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} }{\mathrm{2}^{{n}} }\right)\:\:\:\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} }{\mathrm{2}^{{n}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\frac{{e}^{{ix}} }{\mathrm{2}}\right)^{{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(\frac{{e}^{{ix}} }{\mathrm{2}}\right)^{{n}} \:−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{{e}^{{ix}} }{\mathrm{2}}}\:−\mathrm{1}\:\:\:\:\left(\mid\frac{{e}^{{ix}} }{\mathrm{2}}\mid=\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}−{e}^{{ix}} }\:−\mathrm{1}\:=\frac{\mathrm{2}}{\mathrm{2}−{cosx}\:−{isinx}}\:−\mathrm{1}\:=\frac{\mathrm{2}\left(\mathrm{2}−{cosx}\:+{isinx}\right)}{\left(\mathrm{2}−{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}}\:−\mathrm{1} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}−{cosx}\right)−\left\{\:\left(\mathrm{2}−{cosx}\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} {x}\right\}\:+\mathrm{2}{i}\:{sinx}}{\left(\mathrm{2}−{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${S}\left({x}\right)\:=\frac{\mathrm{4}{sinx}}{\left(\mathrm{2}−{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}}\:=\frac{\mathrm{4}{sinx}}{\mathrm{4}−\mathrm{4}{cosx}\:+\mathrm{1}}\:=\frac{\mathrm{4}{sinx}}{\mathrm{5}−\mathrm{4}{cosx}} \\ $$$${x}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow{S}\left(\frac{\pi}{\mathrm{4}}\right)\:=\frac{\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{5}−\mathrm{4}{cos}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}}{\mathrm{5}−\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}}\:=\frac{\mathrm{4}}{\mathrm{5}\sqrt{\mathrm{2}}−\mathrm{4}}\:. \\ $$
