Menu Close

Question-62613

Tinku Tara 0 Comments
Pin




Question Number 62613 by necx1 last updated on 23/Jun/19
Commented by Prithwish sen last updated on 23/Jun/19
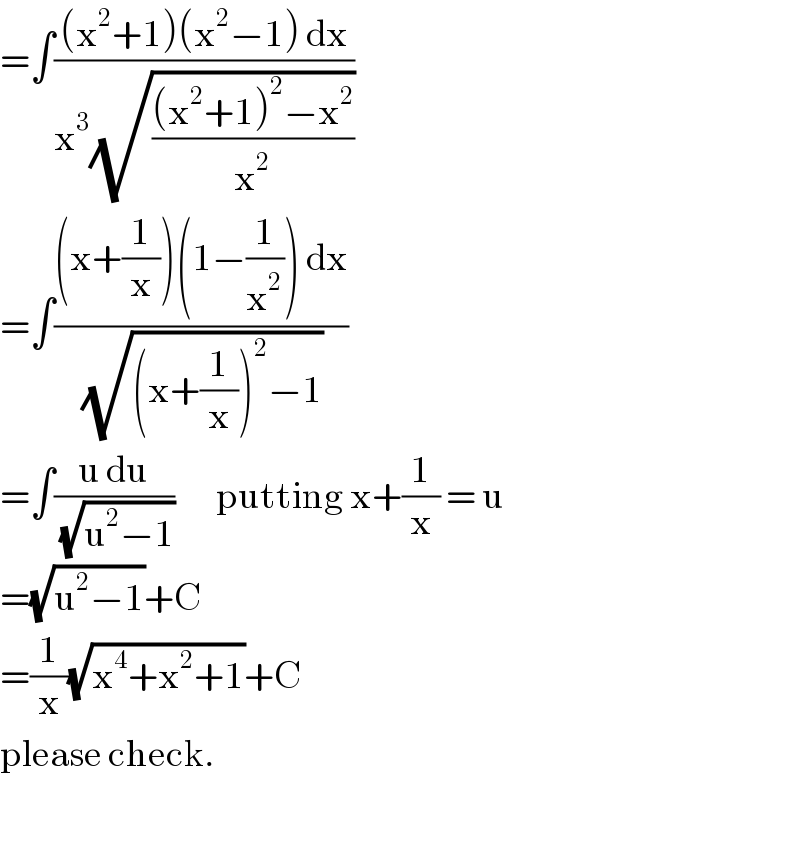
=∫(((x^2 +1)(x^2 −1) dx)/(x^3 (√(((x^2 +1)^2 −x^2 )/x^2 )))) =∫(((x+(1/x))(1−(1/x^2 )) dx)/( (√((x+(1/x))^2 −1)))) =∫((u du)/( (√(u^2 −1)))) putting x+(1/x) = u =(√(u^2 −1))+C =(1/x)(√(x^4 +x^2 +1))+C please check.
$$=\int\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\:\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \sqrt{\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}} \\ $$$$=\int\frac{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\:\mathrm{dx}}{\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\int\frac{\mathrm{u}\:\mathrm{du}}{\:\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}}\:\:\:\:\:\:\:\mathrm{putting}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{u} \\ $$$$=\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{C} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 24/Jun/19
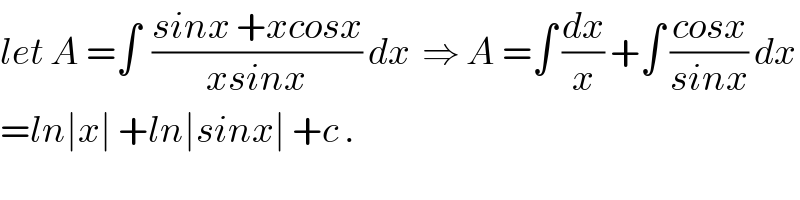
let A =∫ ((sinx +xcosx)/(xsinx)) dx ⇒ A =∫ (dx/x) +∫ ((cosx)/(sinx)) dx =ln∣x∣ +ln∣sinx∣ +c .
$${let}\:{A}\:=\int\:\:\frac{{sinx}\:+{xcosx}}{{xsinx}}\:{dx}\:\:\Rightarrow\:{A}\:=\int\:\frac{{dx}}{{x}}\:+\int\:\frac{{cosx}}{{sinx}}\:{dx} \\ $$$$={ln}\mid{x}\mid\:+{ln}\mid{sinx}\mid\:+{c}\:. \\ $$
Answered by tanmay last updated on 23/Jun/19
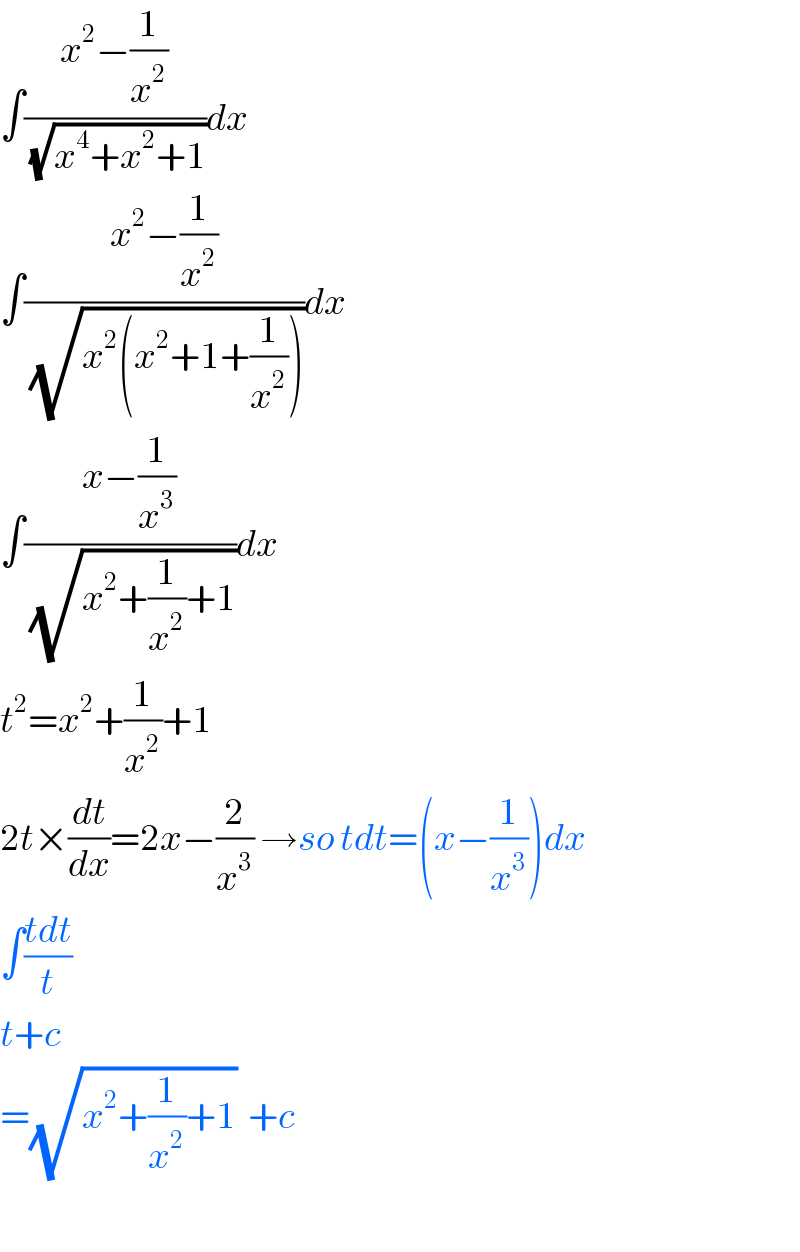
∫((x^2 −(1/x^2 ))/( (√(x^4 +x^2 +1))))dx ∫((x^2 −(1/x^2 ))/( (√(x^2 (x^2 +1+(1/x^2 ))))))dx ∫((x−(1/x^3 ))/( (√(x^2 +(1/x^2 )+1))))dx t^2 =x^2 +(1/x^2 )+1 2t×(dt/dx)=2x−(2/x^3 ) →so tdt=(x−(1/x^3 ))dx ∫((tdt)/t) t+c =(√(x^2 +(1/x^2 )+1)) +c
$$\int\frac{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\:\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\:\sqrt{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}}{dx} \\ $$$$\int\frac{{x}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}{\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}}{dx} \\ $$$${t}^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1} \\ $$$$\mathrm{2}{t}×\frac{{dt}}{{dx}}=\mathrm{2}{x}−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\:\rightarrow{so}\:{tdt}=\left({x}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right){dx} \\ $$$$\int\frac{{tdt}}{{t}} \\ $$$${t}+{c} \\ $$$$=\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}\:\:+{c} \\ $$$$ \\ $$
Answered by som(math1967) last updated on 23/Jun/19
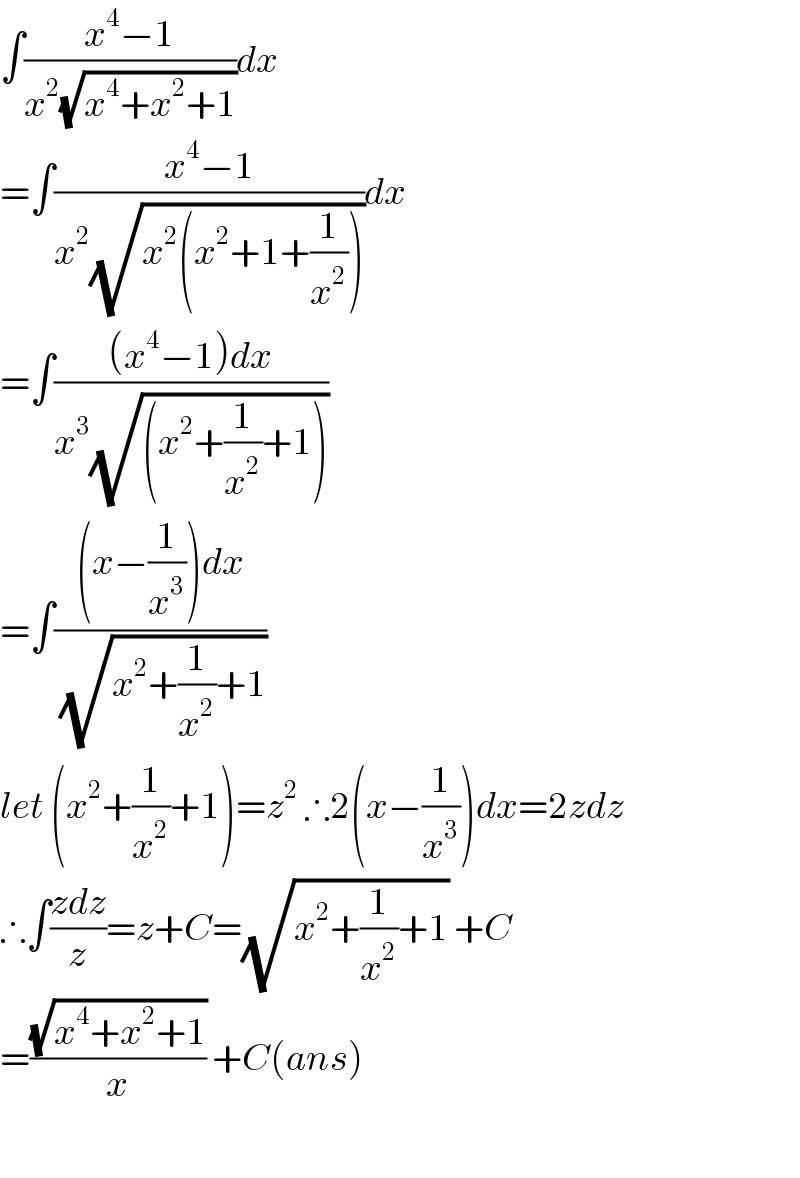
∫((x^4 −1)/(x^2 (√(x^4 +x^2 +1))))dx =∫((x^4 −1)/(x^2 (√(x^2 (x^2 +1+(1/x^2 ))))))dx =∫(((x^4 −1)dx)/(x^3 (√((x^2 +(1/x^2 )+1))))) =∫(((x−(1/x^3 ))dx)/( (√(x^2 +(1/x^2 )+1)))) let (x^2 +(1/x^2 )+1)=z^2 ∴2(x−(1/x^3 ))dx=2zdz ∴∫((zdz)/z)=z+C=(√(x^2 +(1/x^2 )+1)) +C =((√(x^4 +x^2 +1))/x) +C(ans)
$$\int\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$$$=\int\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}}{dx} \\ $$$$=\int\frac{\left({x}^{\mathrm{4}} −\mathrm{1}\right){dx}}{{x}^{\mathrm{3}} \sqrt{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}\right)}} \\ $$$$=\int\frac{\left({x}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right){dx}}{\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}} \\ $$$${let}\:\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}\right)={z}^{\mathrm{2}} \:\therefore\mathrm{2}\left({x}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right){dx}=\mathrm{2}{zdz} \\ $$$$\therefore\int\frac{{zdz}}{{z}}={z}+{C}=\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}\:+{C} \\ $$$$=\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}\:+{C}\left({ans}\right) \\ $$$$ \\ $$
Commented by necx1 last updated on 29/Jun/19
you people are just so wonderful.Thank you so much.
$${you}\:{people}\:{are}\:{just}\:{so}\:{wonderful}.{Thank} \\ $$$${you}\:{so}\:{much}. \\ $$
Answered by MJS last updated on 23/Jun/19
there′s a trick: ∫((x^4 −1)/(x^2 (√(x^4 +x^2 +1))))dx= ∫(((x^4 −1)/(x^2 (√(x^4 +x^2 +1))))+((√(x^4 +x^2 +1))/x^2 )−((√(x^4 +x^2 +1))/x^2 ))dx= =∫((2x^2 +1)/( (√(x^4 +x^2 +1))))dx−∫((√(x^4 +x^2 +1))/x^2 )dx now solve the 2^(nd) integral by parts ∫u′v=uv−∫uv′ u′=(1/x^2 ) ⇒ u=−(1/x) v=(√(x^4 +x^2 +1)) ⇒ v′=((2x^3 +x)/( (√(x^4 +x^2 +1)))) −∫((√(x^4 +x^2 +1))/x^2 )dx=((√(x^4 +x^2 +1))/x)−∫((2x^2 +1)/( (√(x^4 +x^2 +1))))dx ⇒ ∫((x^4 −1)/(x^2 (√(x^4 +x^2 +1))))dx=((√(x^4 +x^2 +1))/x)+C
$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{trick}: \\ $$$$\int\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx}= \\ $$$$\int\left(\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} }−\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} }\right){dx}= \\ $$$$=\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx}−\int\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{integral}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int{u}'{v}={uv}−\int{uv}' \\ $$$${u}'=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\Rightarrow\:{u}=−\frac{\mathrm{1}}{{x}} \\ $$$${v}=\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\:{v}'=\frac{\mathrm{2}{x}^{\mathrm{3}} +{x}}{\:\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$−\int\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} }{dx}=\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}−\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{dx}=\frac{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}+{C} \\ $$
Commented by som(math1967) last updated on 24/Jun/19
Nice sir
$${Nice}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *