Menu Close

Question-62672

Tinku Tara 0 Comments
Pin




Question Number 62672 by bshahid010@gmail.com last updated on 24/Jun/19
Commented by Rasheed.Sindhi last updated on 24/Jun/19
b∈I, I means irrational?
$$\mathrm{b}\in\mathrm{I},\:\mathrm{I}\:{means}\:{irrational}? \\ $$
Commented by mr W last updated on 24/Jun/19
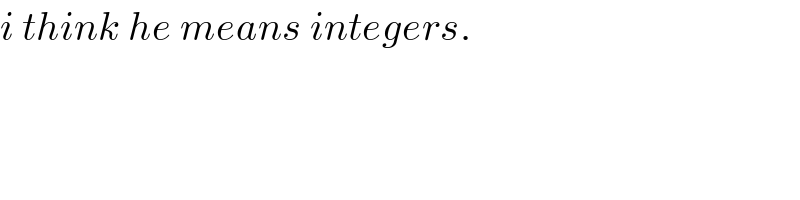
i think he means integers.
$${i}\:{think}\:{he}\:{means}\:{integers}. \\ $$
Commented by MJS last updated on 24/Jun/19
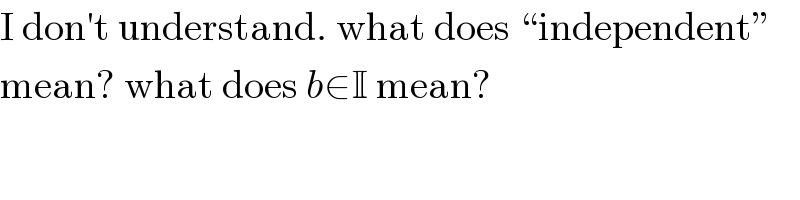
I don′t understand. what does “independent” mean? what does b∈I mean?
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}.\:\mathrm{what}\:\mathrm{does}\:“\mathrm{independent}'' \\ $$$$\mathrm{mean}?\:\mathrm{what}\:\mathrm{does}\:{b}\in\mathbb{I}\:\mathrm{mean}? \\ $$
Commented by mr W last updated on 24/Jun/19
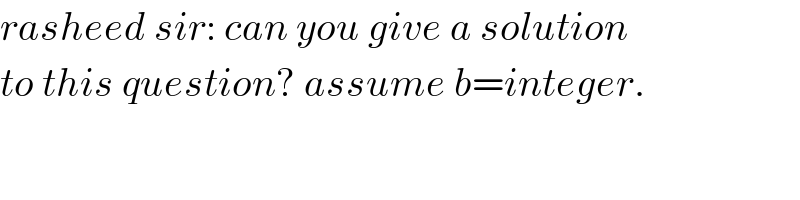
rasheed sir: can you give a solution to this question? assume b=integer.
$${rasheed}\:{sir}:\:{can}\:{you}\:{give}\:{a}\:{solution} \\ $$$${to}\:{this}\:{question}?\:{assume}\:{b}={integer}. \\ $$
Commented by bshahid010@gmail.com last updated on 24/Jun/19
Here I means integer which...I denotes the set of Integers. Independent means that should not be related to each other anyways
$$\mathrm{Here}\:\mathrm{I}\:\mathrm{means}\:\mathrm{integer}\:\mathrm{which}…\mathrm{I}\:\mathrm{denotes}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{Integers}. \\ $$$$\mathrm{Independent}\:\mathrm{means}\:\mathrm{that}\:\mathrm{should}\:\mathrm{not}\:\mathrm{be}\:\mathrm{related}\:\mathrm{to}\:\mathrm{each} \\ $$$$\mathrm{other}\:\mathrm{anyways} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/19
Counter Example a=8(integer),b=3(odd prime),c=5(odd prime b^2 −4ac=8^2 −4(3)(5)=4 perfect square ⇒ Roots are rational (Yet both roots are dependant on a,b,c dependant in a sense that their solution involve the above values of a,b & c ???) x=((−3±2)/(2(8)))=−(1/(16)),−(5/(16)) Actually roots are always dependant on a,b & c. So it′s questionable to say about roots which are independant of a,b,c.
$${Counter}\:{Example} \\ $$$${a}=\mathrm{8}\left({integer}\right),{b}=\mathrm{3}\left({odd}\:{prime}\right),{c}=\mathrm{5}\left({odd}\:{prime}\right. \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{8}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{3}\right)\left(\mathrm{5}\right)=\mathrm{4}\:{perfect}\:{square} \\ $$$$\Rightarrow\:{Roots}\:{are}\:{rational} \\ $$$$\left({Yet}\:{both}\:{roots}\:{are}\:{dependant}\:{on}\:{a},{b},{c}\right. \\ $$$${dependant}\:{in}\:{a}\:{sense}\:{that}\:{their}\:{solution} \\ $$$$\left.{involve}\:{the}\:{above}\:{values}\:{of}\:{a},{b}\:\&\:{c}\:???\right) \\ $$$$ \\ $$$${x}=\frac{−\mathrm{3}\pm\mathrm{2}}{\mathrm{2}\left(\mathrm{8}\right)}=−\frac{\mathrm{1}}{\mathrm{16}},−\frac{\mathrm{5}}{\mathrm{16}} \\ $$$${Actually}\:{roots}\:{are}\:{always}\:{dependant} \\ $$$${on}\:{a},{b}\:\&\:{c}.\:{So}\:{it}'{s}\:{questionable}\:{to}\:{say} \\ $$$${about}\:{roots}\:{which}\:{are}\:{independant} \\ $$$${of}\:{a},{b},{c}. \\ $$$$ \\ $$
Commented by mr W last updated on 24/Jun/19
i think it is meant that one of the roots is a constant no matter which values a,b,c are of. in your example: a=3,b=8,c=5 b^2 −4ac=4 x=((−8±2)/6)=−1,−(5/3) i.e. x=−1,−(c/a) i think one root is always −1, independently from the values of a,b,c.
$${i}\:{think}\:{it}\:{is}\:{meant}\:{that}\:{one}\:{of}\:{the} \\ $$$${roots}\:{is}\:{a}\:{constant}\:{no}\:{matter}\:{which} \\ $$$${values}\:{a},{b},{c}\:{are}\:{of}. \\ $$$${in}\:{your}\:{example}: \\ $$$${a}=\mathrm{3},{b}=\mathrm{8},{c}=\mathrm{5} \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{4} \\ $$$${x}=\frac{−\mathrm{8}\pm\mathrm{2}}{\mathrm{6}}=−\mathrm{1},−\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${i}.{e}.\:{x}=−\mathrm{1},−\frac{{c}}{{a}} \\ $$$${i}\:{think}\:{one}\:{root}\:{is}\:{always}\:−\mathrm{1}, \\ $$$${independently}\:{from}\:{the}\:{values}\:{of} \\ $$$${a},{b},{c}. \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/19
Sir, these two examples prove that neither of the roots is constant,although we have fulfilled all the requirements: b integer, a,c odd primes and rational roots. b=8,a=3,b=5 b=8,a=5,b=3 ⇒ In both cases roots are rational But no root is same!
$$\boldsymbol{{Sir}},\:{these}\:{two}\:{examples}\:{prove}\:{that} \\ $$$${neither}\:{of}\:{the}\:{roots}\:{is}\:{constant},{although} \\ $$$${we}\:{have}\:{fulfilled}\:{all}\:{the}\:{requirements}: \\ $$$${b}\:{integer},\:{a},{c}\:{odd}\:{primes}\:{and}\:{rational} \\ $$$${roots}. \\ $$$${b}=\mathrm{8},{a}=\mathrm{3},{b}=\mathrm{5} \\ $$$${b}=\mathrm{8},{a}=\mathrm{5},{b}=\mathrm{3} \\ $$$$\Rightarrow\:{In}\:{both}\:{cases}\:{roots}\:{are}\:{rational} \\ $$$${But}\:{no}\:{root}\:{is}\:{same}! \\ $$
Commented by MJS last updated on 24/Jun/19
a=p c=p±2n b=±2(n+p) ⇒ x=∓1∨x=∓((2n+p)/p) b=±[p(2n+p)+1] ⇒ x=∓(2n+p)∨x=∓(1/p)
$${a}={p}\:{c}={p}\pm\mathrm{2}{n} \\ $$$$\:\:\:\:\:{b}=\pm\mathrm{2}\left({n}+{p}\right)\:\Rightarrow\:{x}=\mp\mathrm{1}\vee{x}=\mp\frac{\mathrm{2}{n}+{p}}{{p}} \\ $$$$\:\:\:\:\:{b}=\pm\left[{p}\left(\mathrm{2}{n}+{p}\right)+\mathrm{1}\right]\:\Rightarrow\:{x}=\mp\left(\mathrm{2}{n}+{p}\right)\vee{x}=\mp\frac{\mathrm{1}}{{p}} \\ $$
Answered by mr W last updated on 24/Jun/19
x=((−b±(√(b^2 −4ac)))/(2a))=((−b±n)/(2a)) b^2 −4ac=n^2 , say b^2 −n^2 =4ac (b−n)(b+n)=4ac=2^2 a^1 c^1 ⇒b and n must be both even or odd. i.e. b−n and b+n must be even. since a and c are odd primes, RHS has 3×2×2=12 factors, or it can be expressed as the product of two numbers in 6 ways: 4ac=1×4ac=2×2ac=4×ac=a×4c=2a×2c=4a×c case 1: { ((b−n=1 ⇒ bad!)),((b+n=4ac)) :} case 2: { ((b−n=2 ⇒ b=ac+1, n=ac−1)),((b+n=2ac)) :} case 2′: { ((b−n=2ac ⇒ b=ac+1, n=1−ac)),((b+n=2)) :} case 3: { ((b−n=4)),((b+n=ac ⇒ bad!)) :} case 4: { ((b−n=a ⇒ bad!)),((b+n=4c)) :} case 5: { ((b−n=2a ⇒ b=c+a, n=c−a)),((b+n=2c)) :} case 5′: { ((b−n=2c ⇒ b=c+a, n=a−c)),((b+n=2a)) :} case 6: { ((b−n=4a)),((b+n=c ⇒ bad!)) :} we see only case 2 and case 5 are suitable. from case 2+2′: b=ac+1 x=((−b±n)/(2a))=((−ac−1±(1−ac))/(2a))= { ((−(1/a))),((−c)) :} from case 5+5′: b=a+c x=((−b±n)/(2a))=((−c−a±(c−a))/(2a))= { ((−1)),((−(c/a))) :} summary: to fulfill the condictions, b must be ac+1 or a+c. with b=a+c, one root is always −1. but with b=ac+1, both roots are dependent from a and c, that is to say the question is not correct!
$${x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}}=\frac{−{b}\pm{n}}{\mathrm{2}{a}} \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}={n}^{\mathrm{2}} ,\:{say} \\ $$$${b}^{\mathrm{2}} −{n}^{\mathrm{2}} =\mathrm{4}{ac} \\ $$$$\left({b}−{n}\right)\left({b}+{n}\right)=\mathrm{4}{ac}=\mathrm{2}^{\mathrm{2}} {a}^{\mathrm{1}} {c}^{\mathrm{1}} \\ $$$$\Rightarrow{b}\:{and}\:{n}\:{must}\:{be}\:{both}\:{even}\:{or}\:{odd}. \\ $$$${i}.{e}.\:{b}−{n}\:{and}\:{b}+{n}\:{must}\:{be}\:{even}. \\ $$$${since}\:{a}\:{and}\:{c}\:{are}\:{odd}\:{primes},\:{RHS} \\ $$$${has}\:\mathrm{3}×\mathrm{2}×\mathrm{2}=\mathrm{12}\:{factors},\:{or}\:{it}\:{can} \\ $$$${be}\:{expressed}\:{as}\:{the}\:{product}\:{of}\:{two} \\ $$$${numbers}\:{in}\:\mathrm{6}\:{ways}: \\ $$$$\mathrm{4}{ac}=\mathrm{1}×\mathrm{4}{ac}=\mathrm{2}×\mathrm{2}{ac}=\mathrm{4}×{ac}={a}×\mathrm{4}{c}=\mathrm{2}{a}×\mathrm{2}{c}=\mathrm{4}{a}×{c} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:\begin{cases}{{b}−{n}=\mathrm{1}\:\Rightarrow\:{bad}!}\\{{b}+{n}=\mathrm{4}{ac}}\end{cases} \\ $$$${case}\:\mathrm{2}:\:\begin{cases}{{b}−{n}=\mathrm{2}\:\Rightarrow\:{b}={ac}+\mathrm{1},\:{n}={ac}−\mathrm{1}}\\{{b}+{n}=\mathrm{2}{ac}}\end{cases} \\ $$$${case}\:\mathrm{2}':\:\begin{cases}{{b}−{n}=\mathrm{2}{ac}\:\Rightarrow\:{b}={ac}+\mathrm{1},\:{n}=\mathrm{1}−{ac}}\\{{b}+{n}=\mathrm{2}}\end{cases} \\ $$$${case}\:\mathrm{3}:\:\begin{cases}{{b}−{n}=\mathrm{4}}\\{{b}+{n}={ac}\:\Rightarrow\:{bad}!}\end{cases} \\ $$$${case}\:\mathrm{4}:\:\begin{cases}{{b}−{n}={a}\:\Rightarrow\:{bad}!}\\{{b}+{n}=\mathrm{4}{c}}\end{cases} \\ $$$${case}\:\mathrm{5}:\:\begin{cases}{{b}−{n}=\mathrm{2}{a}\:\Rightarrow\:{b}={c}+{a},\:{n}={c}−{a}}\\{{b}+{n}=\mathrm{2}{c}}\end{cases} \\ $$$${case}\:\mathrm{5}':\:\begin{cases}{{b}−{n}=\mathrm{2}{c}\:\Rightarrow\:{b}={c}+{a},\:{n}={a}−{c}}\\{{b}+{n}=\mathrm{2}{a}}\end{cases} \\ $$$${case}\:\mathrm{6}:\:\begin{cases}{{b}−{n}=\mathrm{4}{a}}\\{{b}+{n}={c}\:\Rightarrow\:{bad}!}\end{cases} \\ $$$${we}\:{see}\:{only}\:{case}\:\mathrm{2}\:{and}\:{case}\:\mathrm{5}\:{are}\:{suitable}. \\ $$$$ \\ $$$${from}\:{case}\:\mathrm{2}+\mathrm{2}': \\ $$$${b}={ac}+\mathrm{1} \\ $$$${x}=\frac{−{b}\pm{n}}{\mathrm{2}{a}}=\frac{−{ac}−\mathrm{1}\pm\left(\mathrm{1}−{ac}\right)}{\mathrm{2}{a}}=\begin{cases}{−\frac{\mathrm{1}}{{a}}}\\{−{c}}\end{cases} \\ $$$${from}\:{case}\:\mathrm{5}+\mathrm{5}': \\ $$$${b}={a}+{c} \\ $$$${x}=\frac{−{b}\pm{n}}{\mathrm{2}{a}}=\frac{−{c}−{a}\pm\left({c}−{a}\right)}{\mathrm{2}{a}}=\begin{cases}{−\mathrm{1}}\\{−\frac{{c}}{{a}}}\end{cases} \\ $$$$ \\ $$$${summary}: \\ $$$${to}\:{fulfill}\:{the}\:{condictions},\:{b}\:{must} \\ $$$${be}\:{ac}+\mathrm{1}\:{or}\:{a}+{c}.\:{with}\:{b}={a}+{c},\:{one} \\ $$$${root}\:{is}\:{always}\:−\mathrm{1}.\:{but}\:{with}\:{b}={ac}+\mathrm{1}, \\ $$$${both}\:{roots}\:{are}\:{dependent}\:{from}\:{a}\:{and}\:{c}, \\ $$$${that}\:{is}\:{to}\:{say}\:{the}\:{question}\:{is}\:{not} \\ $$$${correct}! \\ $$
Commented by Rasheed.Sindhi last updated on 24/Jun/19
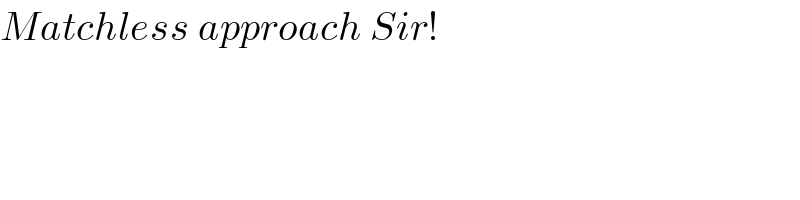
Matchless approach Sir!
$${Matchless}\:{approach}\:{Sir}! \\ $$
Commented by mr W last updated on 24/Jun/19
thanks sir! but i just proved that the question is not correct.
$${thanks}\:{sir}!\:{but}\:{i}\:{just}\:{proved}\:{that}\:{the} \\ $$$${question}\:{is}\:{not}\:{correct}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *