Menu Close

Question-62821

Tinku Tara 0 Comments
Pin




Question Number 62821 by ajfour last updated on 25/Jun/19
Commented by ajfour last updated on 25/Jun/19
If the right circular cone contains half the spherical volume within its lateral surface, find 𝛂.
$${If}\:{the}\:{right}\:{circular}\:{cone}\:{contains} \\ $$$${half}\:{the}\:{spherical}\:{volume}\:{within} \\ $$$${its}\:{lateral}\:{surface},\:{find}\:\boldsymbol{\alpha}. \\ $$
Answered by ajfour last updated on 25/Jun/19
Commented by ajfour last updated on 25/Jun/19
spherical cap volume S S=∫_(h=cos 2Ξ±) ^( 1) Ο€(1βˆ’z^2 )dz = Ο€{zβˆ’(z^3 /3)}∣_h ^1 = ((2Ο€)/3)βˆ’Ο€(hβˆ’(h^3 /3)) Conical volume C C = (Ο€/3)r^2 (h+1) And r=htan 2Ξ± Now S+C=((2Ο€)/3) (half spherical volume) β‡’((2Ο€)/3)βˆ’Ο€(hβˆ’(h^3 /3))+(Ο€/3)r^2 (h+1)=((2Ο€)/3) β‡’ hβˆ’(h^3 /3)=((h^2 (h+1)tan^2 2Ξ±)/3) β‡’ 3βˆ’h^2 =(h^2 +h)(sec^2 2Ξ±βˆ’1) And as h=cos 2Ξ± 3βˆ’h^2 =h(h+1)((1/h^2 )βˆ’1) β‡’ 3hβˆ’h^3 =(h+1)(1βˆ’h^2 ) β‡’ 3hβˆ’h^3 =h+1βˆ’h^3 βˆ’h^2 β‡’ h^2 +2hβˆ’1=0 β‡’ h=((βˆ’2+(√(4+4)))/2) = (√2)βˆ’1 2cos^2 Ξ±βˆ’1=(√2)βˆ’1 β‡’ Ξ± = cos^(βˆ’1) (1/(2)^(1/4) ) .
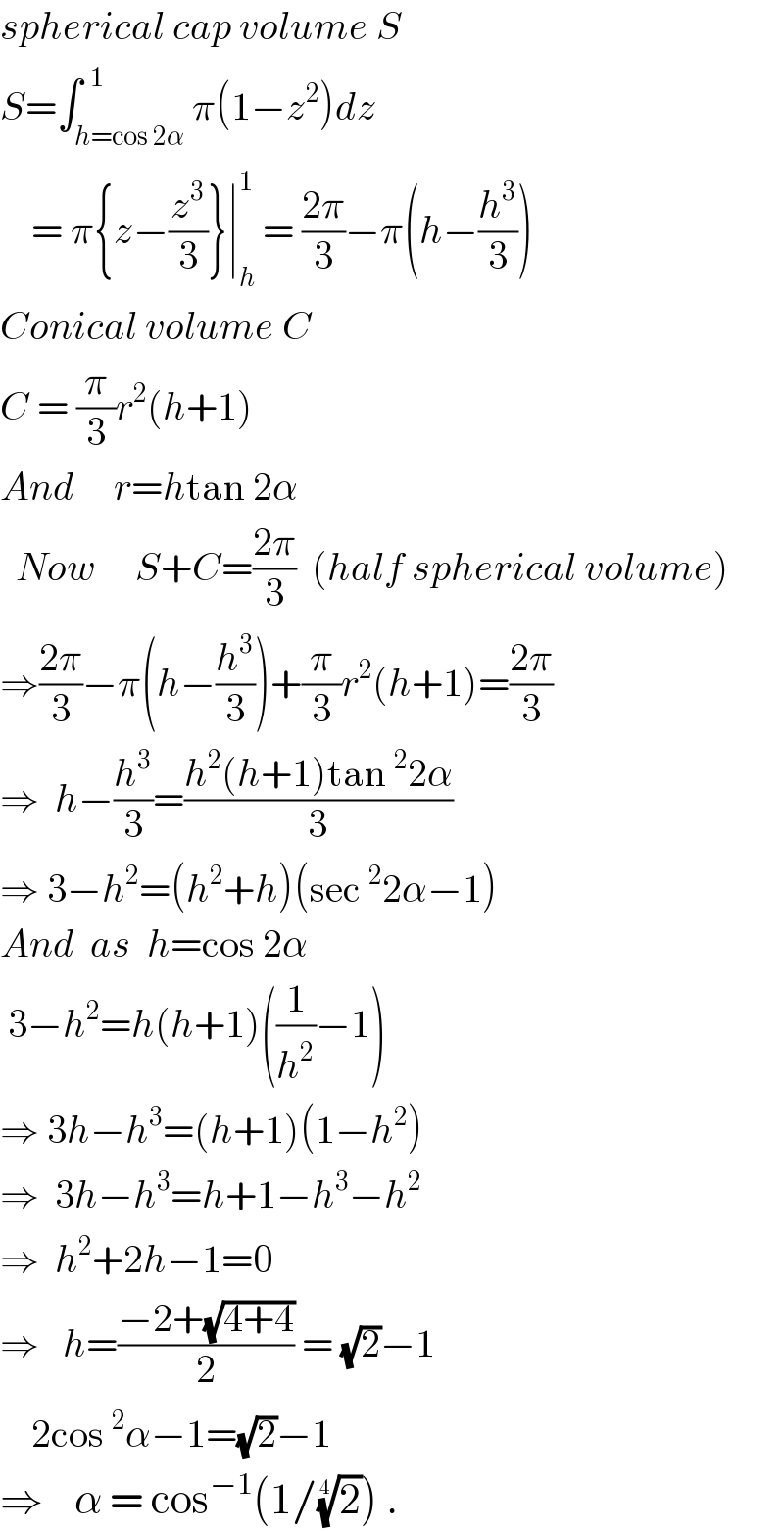
$${spherical}\:{cap}\:{volume}\:{S} \\ $$$${S}=\int_{{h}=\mathrm{cos}\:\mathrm{2}\alpha} ^{\:\:\mathrm{1}} \pi\left(\mathrm{1}βˆ’{z}^{\mathrm{2}} \right){dz} \\ $$$$\:\:\:\:=\:\pi\left\{{z}βˆ’\frac{{z}^{\mathrm{3}} }{\mathrm{3}}\right\}\mid_{{h}} ^{\mathrm{1}} \:=\:\frac{\mathrm{2}\pi}{\mathrm{3}}βˆ’\pi\left({h}βˆ’\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$${Conical}\:{volume}\:{C} \\ $$$${C}\:=\:\frac{\pi}{\mathrm{3}}{r}^{\mathrm{2}} \left({h}+\mathrm{1}\right) \\ $$$${And}\:\:\:\:\:{r}={h}\mathrm{tan}\:\mathrm{2}\alpha \\ $$$$\:\:{Now}\:\:\:\:\:{S}+{C}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\:\left({half}\:{spherical}\:{volume}\right) \\ $$$$\Rightarrow\frac{\mathrm{2}\pi}{\mathrm{3}}βˆ’\pi\left({h}βˆ’\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\right)+\frac{\pi}{\mathrm{3}}{r}^{\mathrm{2}} \left({h}+\mathrm{1}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\:\:{h}βˆ’\frac{{h}^{\mathrm{3}} }{\mathrm{3}}=\frac{{h}^{\mathrm{2}} \left({h}+\mathrm{1}\right)\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}\alpha}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{3}βˆ’{h}^{\mathrm{2}} =\left({h}^{\mathrm{2}} +{h}\right)\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}\alphaβˆ’\mathrm{1}\right) \\ $$$${And}\:\:{as}\:\:{h}=\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$\:\mathrm{3}βˆ’{h}^{\mathrm{2}} ={h}\left({h}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{{h}^{\mathrm{2}} }βˆ’\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{3}{h}βˆ’{h}^{\mathrm{3}} =\left({h}+\mathrm{1}\right)\left(\mathrm{1}βˆ’{h}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{3}{h}βˆ’{h}^{\mathrm{3}} ={h}+\mathrm{1}βˆ’{h}^{\mathrm{3}} βˆ’{h}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{h}^{\mathrm{2}} +\mathrm{2}{h}βˆ’\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{h}=\frac{βˆ’\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{4}}}{\mathrm{2}}\:=\:\sqrt{\mathrm{2}}βˆ’\mathrm{1} \\ $$$$\:\:\:\:\mathrm{2cos}\:^{\mathrm{2}} \alphaβˆ’\mathrm{1}=\sqrt{\mathrm{2}}βˆ’\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\alpha\:=\:\mathrm{cos}^{βˆ’\mathrm{1}} \left(\mathrm{1}/\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)\:. \\ $$
Answered by mr W last updated on 25/Jun/19
R=radius of sphere k=height of cone h=height of cap=2Rβˆ’k r=radius of section circle cone / sphere (r/k)=((2Rβˆ’k)/r) β‡’r^2 =k(2Rβˆ’k) volume of cone=((Ο€r^2 k)/3)=((Ο€k^2 (2Rβˆ’k))/3) volume of cap=((Ο€h^2 (3Rβˆ’h))/3)=((Ο€(2Rβˆ’k)^2 (R+k))/3) volume of sphere=((4Ο€R^3 )/3) ((Ο€k^2 (2Rβˆ’k))/3)+((Ο€(2Rβˆ’k)^2 (R+k))/3)=(1/2)Γ—((4Ο€R^3 )/3) (2Rβˆ’k)(2R+k)=2R^2 4R^2 βˆ’k^2 =2R^2 β‡’k=(√2)R k=2R cos^2 Ξ±=(√2)R β‡’cos^2 Ξ±=(1/( (√2))) β‡’Ξ±=cos^(βˆ’1) (1/( (2)^(1/4) ))
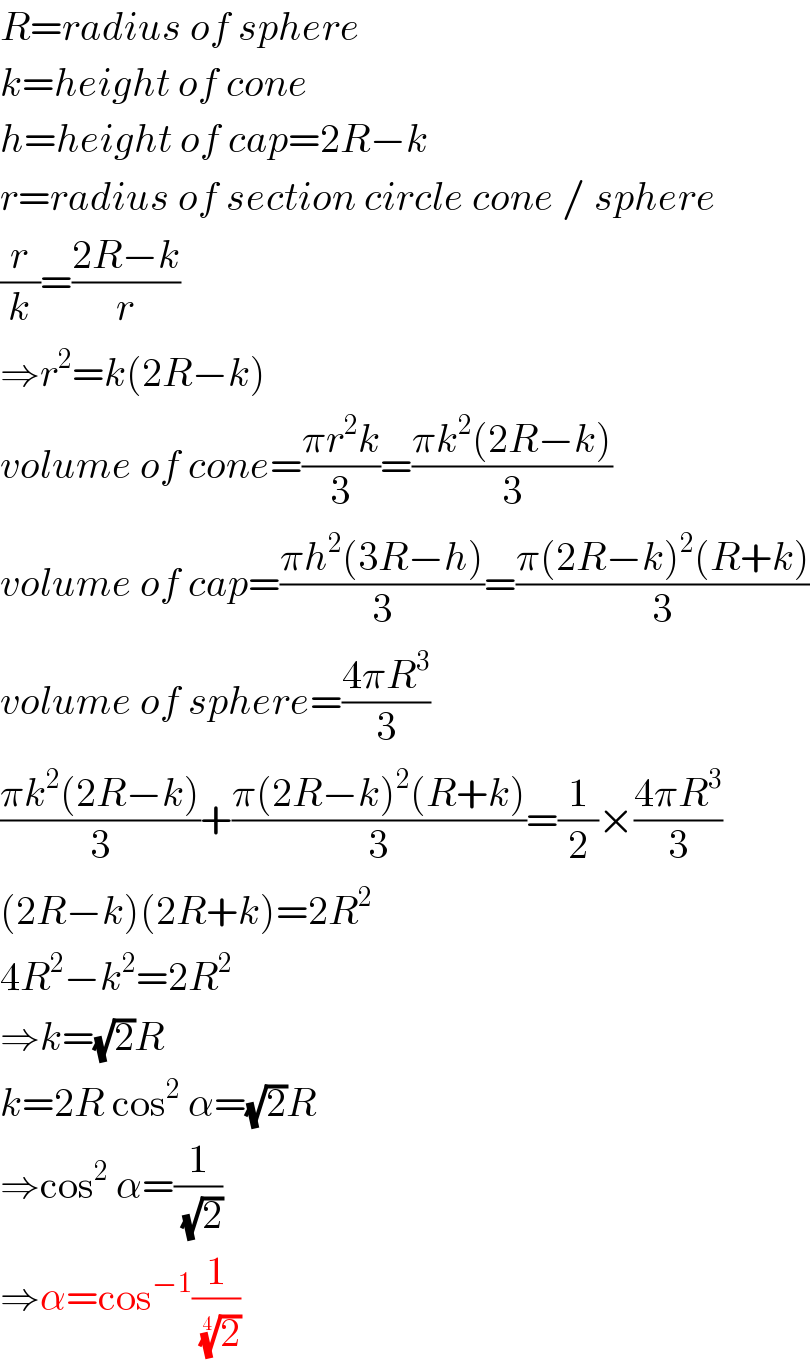
$${R}={radius}\:{of}\:{sphere} \\ $$$${k}={height}\:{of}\:{cone} \\ $$$${h}={height}\:{of}\:{cap}=\mathrm{2}{R}βˆ’{k} \\ $$$${r}={radius}\:{of}\:{section}\:{circle}\:{cone}\:/\:{sphere} \\ $$$$\frac{{r}}{{k}}=\frac{\mathrm{2}{R}βˆ’{k}}{{r}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={k}\left(\mathrm{2}{R}βˆ’{k}\right) \\ $$$${volume}\:{of}\:{cone}=\frac{\pi{r}^{\mathrm{2}} {k}}{\mathrm{3}}=\frac{\pi{k}^{\mathrm{2}} \left(\mathrm{2}{R}βˆ’{k}\right)}{\mathrm{3}} \\ $$$${volume}\:{of}\:{cap}=\frac{\pi{h}^{\mathrm{2}} \left(\mathrm{3}{R}βˆ’{h}\right)}{\mathrm{3}}=\frac{\pi\left(\mathrm{2}{R}βˆ’{k}\right)^{\mathrm{2}} \left({R}+{k}\right)}{\mathrm{3}} \\ $$$${volume}\:{of}\:{sphere}=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\frac{\pi{k}^{\mathrm{2}} \left(\mathrm{2}{R}βˆ’{k}\right)}{\mathrm{3}}+\frac{\pi\left(\mathrm{2}{R}βˆ’{k}\right)^{\mathrm{2}} \left({R}+{k}\right)}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}}Γ—\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\left(\mathrm{2}{R}βˆ’{k}\right)\left(\mathrm{2}{R}+{k}\right)=\mathrm{2}{R}^{\mathrm{2}} \\ $$$$\mathrm{4}{R}^{\mathrm{2}} βˆ’{k}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\sqrt{\mathrm{2}}{R} \\ $$$${k}=\mathrm{2}{R}\:\mathrm{cos}^{\mathrm{2}} \:\alpha=\sqrt{\mathrm{2}}{R} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{βˆ’\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 25/Jun/19
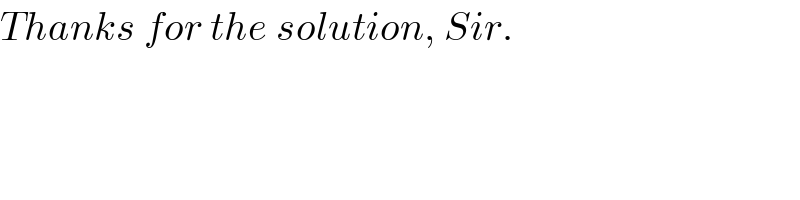
Thanks for the solution, Sir.
$${Thanks}\:{for}\:{the}\:{solution},\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *