Question Number 62850 by ajfour last updated on 25/Jun/19
Commented by ajfour last updated on 25/Jun/19

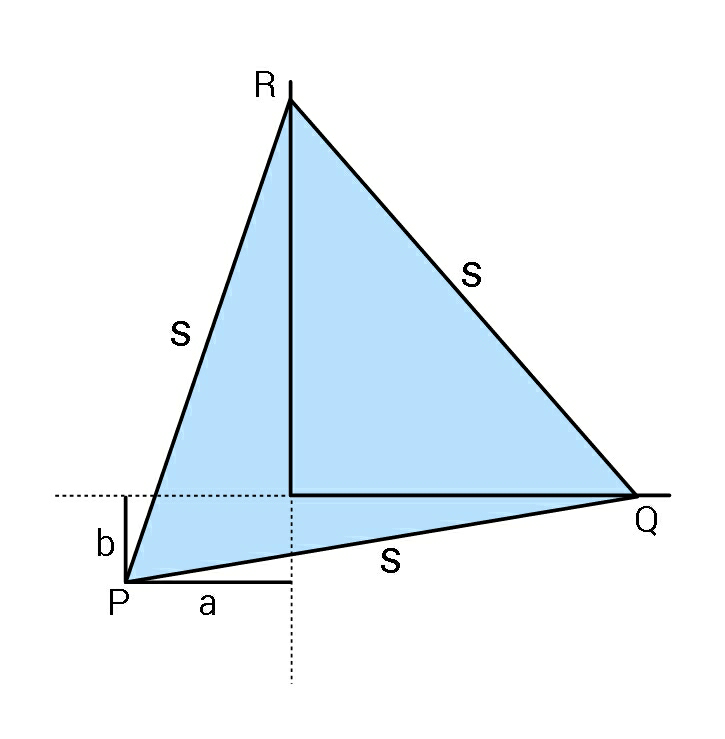
$${Find}\:{possible}\:{values}\:{of}\:{side}\:\boldsymbol{{s}}\:{of} \\ $$$${equilateral}\:\bigtriangleup{PQR}\:{in}\:{terms}\:{of} \\ $$$${a}\:{and}\:{b}.\left({for}\:{example}\:{let}\:{a}=\mathrm{4},\:{b}=\mathrm{3}\right). \\ $$
Answered by mr W last updated on 26/Jun/19
![Q(u,0) R(v,0) t=s^2 =(u+a)^2 +b^2 =(v+b)^2 +a^2 =u^2 +v^2 ⇒u=(√(t−b^2 ))−a ⇒v=(√(t−a^2 ))−b ⇒t−b^2 +a^2 −2a(√(t−b^2 ))+t−a^2 +b^2 −2b(√(t−a^2 ))=t ⇒t−2a(√(t−b^2 ))=2b(√(t−a^2 )) ⇒t^2 −4at(√(t−b^2 ))+4a^2 (t−b^2 )=4b^2 (t−a^2 ) ⇒t+4(a^2 −b^2 )=4a(√(t−b^2 )) ⇒t^2 +8(a^2 −b^2 )t+16(a^2 −b^2 )^2 =16a^2 (t−b^2 ) ⇒t^2 −8(a^2 +b^2 )t+16[(a^2 −b^2 )^2 +a^2 b^2 ]=0 ⇒t=4(a^2 +b^2 )±(√(16(a^2 +b^2 )^2 −16(a^2 −b^2 )^2 −16a^2 b^2 )) ⇒t=4(a^2 +b^2 ±(√3)ab) ⇒s=2(√(a^2 +b^2 ±(√3)ab))](https://www.tinkutara.com/question/Q62858.png)
$${Q}\left({u},\mathrm{0}\right) \\ $$$${R}\left({v},\mathrm{0}\right) \\ $$$${t}={s}^{\mathrm{2}} =\left({u}+{a}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({v}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} ={u}^{\mathrm{2}} +{v}^{\mathrm{2}} \\ $$$$\Rightarrow{u}=\sqrt{{t}−{b}^{\mathrm{2}} }−{a} \\ $$$$\Rightarrow{v}=\sqrt{{t}−{a}^{\mathrm{2}} }−{b} \\ $$$$\Rightarrow{t}−{b}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{a}\sqrt{{t}−{b}^{\mathrm{2}} }+{t}−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{t}−{a}^{\mathrm{2}} }={t} \\ $$$$\Rightarrow{t}−\mathrm{2}{a}\sqrt{{t}−{b}^{\mathrm{2}} }=\mathrm{2}{b}\sqrt{{t}−{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{4}{at}\sqrt{{t}−{b}^{\mathrm{2}} }+\mathrm{4}{a}^{\mathrm{2}} \left({t}−{b}^{\mathrm{2}} \right)=\mathrm{4}{b}^{\mathrm{2}} \left({t}−{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{t}+\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{4}{a}\sqrt{{t}−{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}^{\mathrm{2}} +\mathrm{8}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}+\mathrm{16}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{16}{a}^{\mathrm{2}} \left({t}−{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{8}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){t}+\mathrm{16}\left[\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\pm\sqrt{\mathrm{16}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{16}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}=\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \pm\sqrt{\mathrm{3}}{ab}\right) \\ $$$$\Rightarrow{s}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \pm\sqrt{\mathrm{3}}{ab}} \\ $$
Commented by ajfour last updated on 26/Jun/19
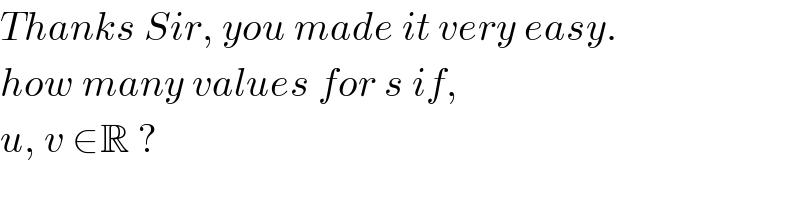
$${Thanks}\:{Sir},\:{you}\:{made}\:{it}\:{very}\:{easy}. \\ $$$${how}\:{many}\:{values}\:{for}\:{s}\:{if}, \\ $$$${u},\:{v}\:\in\mathbb{R}\:? \\ $$
Commented by mr W last updated on 26/Jun/19
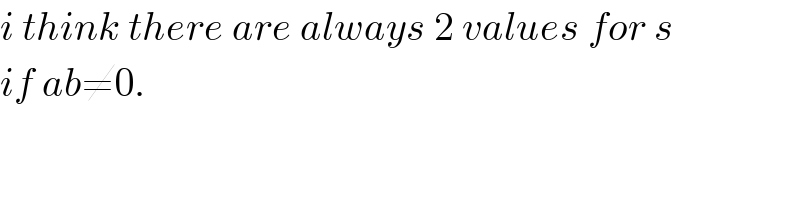
$${i}\:{think}\:{there}\:{are}\:{always}\:\mathrm{2}\:{values}\:{for}\:{s}\: \\ $$$${if}\:{ab}\neq\mathrm{0}. \\ $$
Commented by ajfour last updated on 26/Jun/19
yes sir, i am inclined to believe it.
