Question Number 62861 by ajfour last updated on 26/Jun/19
Commented by mr W last updated on 26/Jun/19
$${very}\:{hard}\:{task}\:{sir},\:{maybe}\:{not} \\ $$$${possible}\:{to}\:{solve}. \\ $$
Commented by ajfour last updated on 26/Jun/19
$${seriously}\:{Sir},\:{no}\:{matter}\:{what}\:{i}\:{try}, \\ $$$${it}\:{dont}\:{simplify},\:{biquadratic} \\ $$$${trouble}. \\ $$
Commented by ajfour last updated on 26/Jun/19
$${Find}\:{x}_{{A}} \left({A}\:{being}\:{lowermost}\:{point}\right) \\ $$$${in}\:{terms}\:{of}\:{s}. \\ $$
Commented by ajfour last updated on 26/Jun/19

$${Good}\:{question},\:\mathcal{GREAT}\:{solution}, \\ $$$${Sir}.\:{Truly}\:{above}\:{all}\:{praise},\:{thanks}\:{a}\:{lot}! \\ $$
Commented by MJS last updated on 26/Jun/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{as}\:\mathrm{always} \\ $$$$\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{geometrical}\:\mathrm{problems} \\ $$
Commented by mr W last updated on 26/Jun/19

$${thanks}\:{to}\:{MJS}\:{sir}!\:{i}\:{think}\:{it}\:{is} \\ $$$${impossible}\:{to}\:{solve}\:{the}\:{problem}\:{with} \\ $$$${given}\:{length}\:{s},\:{since}\:{it}\:{leads}\:{always} \\ $$$${to}\:{a}\:{quartic}\:{equation}\:{which}\:{may}\:{have} \\ $$$${max}.\:\mathrm{4}\:{roots}.\:{actually}\:{i}\:{also}\:{considered} \\ $$$${a}\:{way}\:{to}\:{solve}\:{by}\:{assuming}\:{the} \\ $$$${position}\:{of}\:{BC}\:{and}\:{then}\:{determine} \\ $$$${the}\:{point}\:{A}\:{and}\:{the}\:{length}\:{s}.\:{i}\:{think} \\ $$$${we}\:{can}\:{then}\:{avoid}\:{the}\:{quartic}\:{equations}. \\ $$$${but}\:{i}\:{had}\:{no}\:{time}\:{to}\:{try}\:{it}\:{out}\:{today}. \\ $$$${i}'{ll}\:{take}\:{a}\:{try}\:{this}\:{evening}\:{and}\:{see}\:{if} \\ $$$${i}\:{can}\:{get}\:{the}\:{same}\:{result}\:{as}\:{yours}. \\ $$
Commented by mr W last updated on 27/Jun/19

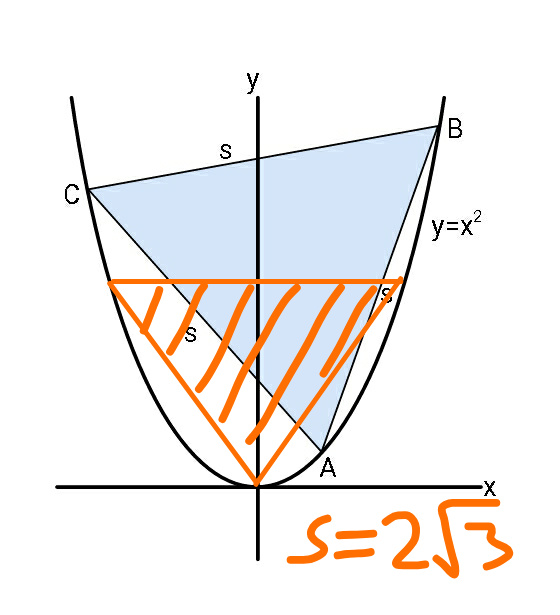
$${MJS}\:{sir}:\:{can}\:{you}\:{please}\:{check}: \\ $$$${i}\:{couldn}'{t}\:{get}\:{the}\:{same}\:{result}\:{as}\:{you}. \\ $$$${according}\:{to}\:{your}\:{result}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}<{a}\leqslant\frac{\sqrt{…}}{\mathrm{3}} \\ $$$${and}\:{i}\:{got}\:\mathrm{0}\leqslant{m}<\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\:\:\left({m}={your}\:{a}\right). \\ $$$${we}\:{know}\:{m}=\mathrm{0}\:{is}\:{possible},\:{because} \\ $$$${the}\:{smallest}\:{equilateral}\:{triangle}\:{is} \\ $$$${s}=\mathrm{2}\sqrt{\mathrm{3}}\:{with}\:{A}\left(\mathrm{0},\mathrm{0}\right),\:{B}\left(\sqrt{\mathrm{3}},\mathrm{3}\right),\:{C}\left(−\sqrt{\mathrm{3}},\mathrm{3}\right). \\ $$$${i}.{e}.\:\mathrm{2}\sqrt{\mathrm{3}}\leqslant{s}<\infty. \\ $$$${but}\:{this}\:{case}\:{is}\:{not}\:{included}\:{in}\:{your} \\ $$$${result},\:{since}\:{you}\:{got}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}<{a}\leqslant\frac{\sqrt{…}}{\mathrm{3}}\:{and} \\ $$$$\mathrm{0}\leqslant{s}<\infty. \\ $$
Commented by mr W last updated on 27/Jun/19
Commented by MJS last updated on 27/Jun/19

$$\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake},\:\mathrm{hopefully}\:\mathrm{corrected} \\ $$$$\mathrm{everything}.\:\mathrm{it}\:\mathrm{now}\:\mathrm{looks}\:\mathrm{as}\:\mathrm{if}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\mathrm{it}\:\mathrm{for}\:{a}={f}\left({s}\right).\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of} \\ $$$$\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{for}\:{a}^{\mathrm{2}} .\:\mathrm{please}\:\mathrm{check}\:\mathrm{my}\:\mathrm{work},\:\mathrm{I}'\mathrm{ve} \\ $$$$\mathrm{been}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry}… \\ $$
Commented by mr W last updated on 27/Jun/19

$${thank}\:{you}\:{sir}! \\ $$$${i}\:{can}\:{not}\:{get}\:{your}\:{formula}\:{for}\:{b}, \\ $$$${but}\:{it}\:{seems}\:{to}\:{be}\:{correct}. \\ $$
Answered by ajfour last updated on 26/Jun/19
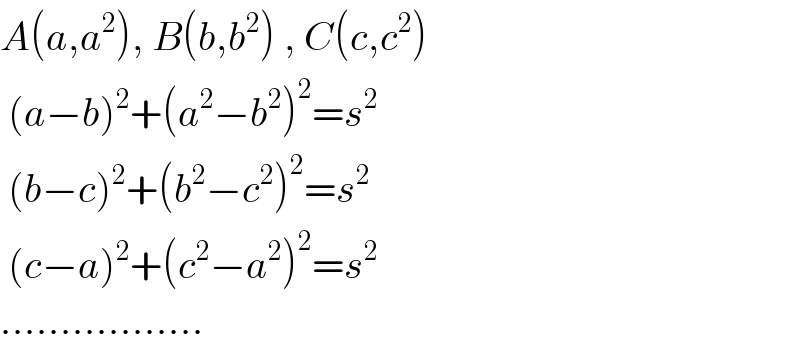
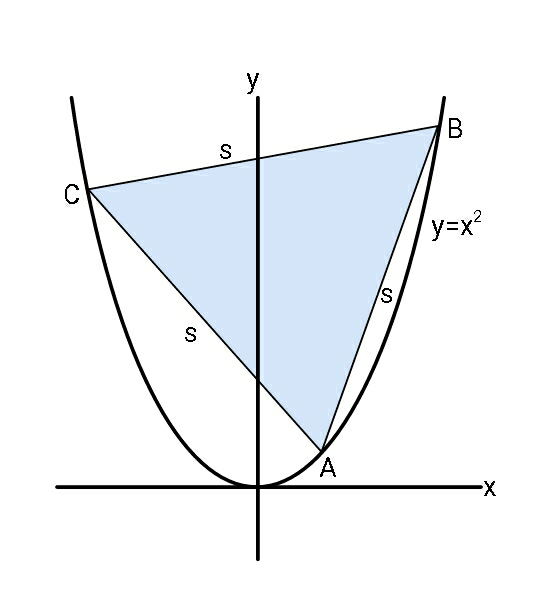
$${A}\left({a},{a}^{\mathrm{2}} \right),\:{B}\left({b},{b}^{\mathrm{2}} \right)\:,\:{C}\left({c},{c}^{\mathrm{2}} \right) \\ $$$$\:\left({a}−{b}\right)^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\:\left({b}−{c}\right)^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\:\left({c}−{a}\right)^{\mathrm{2}} +\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$…………….. \\ $$
Answered by mr W last updated on 26/Jun/19
Commented by mr W last updated on 27/Jun/19
![D(0,h) m=tan θ>0 eqn. of BC: y=h+mx intersection BC with parabola: y=x^2 =h+mx ⇒x^2 −mx−h=0 x_C =((m−(√(m^2 +4h)))/2) x_B =((m+(√(m^2 +4h)))/2) midpoint of BC=M x_M =((x_C +x_B )/2)=(m/2) y_M =((x_C ^2 +x_B ^2 )/2)=(((x_C +x_B )^2 −2x_C x_B )/2)=((m^2 +2h)/2) eqn. of bisector of BC: y−y_M =−(1/m)(x−x_M ) y−((m^2 +2h)/2)=−(1/m)(x−(m/2)) ⇒y=−(x/m)+((m^2 +2h+1)/2) intersection of bisector with parabola: y=x^2 =−(x/m)+((m^2 +2h+1)/2) ⇒x^2 +(x/m)−((m^2 +2h+1)/2)=0 x_A =(1/(2m))[−1+(√(1+2m^2 (m^2 +2h+1)))] y_A =(1/(2m^2 ))[1+m^2 (m^2 +2h+1)−(√(1+2m^2 (m^2 +2h+1)))] ((√3)/2)×BC=MA ⇒((√3)/2)(x_B −x_C )=y_M −y_A ((√3)/2)(√(m^2 +4h))=(1/2)[m^2 +2h−(1/m^2 )−m^2 −2h−1+(1/m)(√((1/m^2 )+2(m^2 +2h+1)))] ⇒m^2 (√(3(m^2 +4h)))=(√(1+2m^2 (m^2 +2h+1)))−(1+m^2 ) ⇒0≤m<((√3)/3) ⇒h≥3 3m^4 (m^2 +4h)=[1+2m^2 (m^2 +2h+1)+1+2m^2 +m^4 −2(1+m^2 )(√(1+2m^2 (m^2 +2h+1)))] 2(1+m^2 )(√(1+2m^2 (m^2 +2h+1)))=2+4m^2 +3m^4 (1−m^2 )+4m^2 (1−3m^2 )h ⇒16m^4 (1−3m^2 )^2 h^2 +8m^2 {(1−3m^2 )(2+4m^2 +3m^4 −3m^6 )−2(1+m^2 )^2 }h+{(2+4m^2 +3m^4 −3m^6 )^2 −4(1+m^2 )^2 (1+2m^2 +2m^4 )}=0 ⇒16(1−3m^2 )^2 h^2 +8(9m^6 −12m^4 −11m^2 −6)h+m^2 (9m^6 −18m^4 −23m^2 −12)=0 ⇒h=(((−9m^6 +12m^4 +11m^2 +6)+(√((9m^6 −12m^4 −11m^2 −6)^2 −m^2 (1−3m^2 )^2 (9m^6 −18m^4 −23m^2 −12))))/(4(1−3m^2 )^2 )) ... i stop here , hope it′s correct, too hard to simplify ... s=(√(1+m^2 ))(x_B −x_C ) ⇒s=(√((1+m^2 )(m^2 +4h))) ⇒s≥2(√3)](https://www.tinkutara.com/question/Q62899.png)
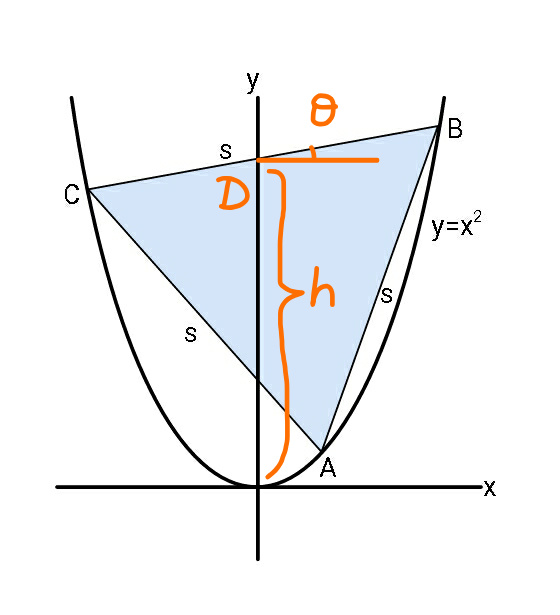
$${D}\left(\mathrm{0},{h}\right) \\ $$$${m}=\mathrm{tan}\:\theta>\mathrm{0} \\ $$$${eqn}.\:{of}\:{BC}: \\ $$$${y}={h}+{mx} \\ $$$${intersection}\:{BC}\:{with}\:{parabola}: \\ $$$${y}={x}^{\mathrm{2}} ={h}+{mx} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{mx}−{h}=\mathrm{0} \\ $$$${x}_{{C}} =\frac{{m}−\sqrt{{m}^{\mathrm{2}} +\mathrm{4}{h}}}{\mathrm{2}} \\ $$$${x}_{{B}} =\frac{{m}+\sqrt{{m}^{\mathrm{2}} +\mathrm{4}{h}}}{\mathrm{2}} \\ $$$${midpoint}\:{of}\:{BC}={M} \\ $$$${x}_{{M}} =\frac{{x}_{{C}} +{x}_{{B}} }{\mathrm{2}}=\frac{{m}}{\mathrm{2}} \\ $$$${y}_{{M}} =\frac{{x}_{{C}} ^{\mathrm{2}} +{x}_{{B}} ^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({x}_{{C}} +{x}_{{B}} \right)^{\mathrm{2}} −\mathrm{2}{x}_{{C}} {x}_{{B}} }{\mathrm{2}}=\frac{{m}^{\mathrm{2}} +\mathrm{2}{h}}{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{bisector}\:{of}\:{BC}: \\ $$$${y}−{y}_{{M}} =−\frac{\mathrm{1}}{{m}}\left({x}−{x}_{{M}} \right) \\ $$$${y}−\frac{{m}^{\mathrm{2}} +\mathrm{2}{h}}{\mathrm{2}}=−\frac{\mathrm{1}}{{m}}\left({x}−\frac{{m}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{y}=−\frac{{x}}{{m}}+\frac{{m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}}{\mathrm{2}} \\ $$$${intersection}\:{of}\:{bisector}\:{with}\:{parabola}: \\ $$$${y}={x}^{\mathrm{2}} =−\frac{{x}}{{m}}+\frac{{m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\frac{{x}}{{m}}−\frac{{m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${x}_{{A}} =\frac{\mathrm{1}}{\mathrm{2}{m}}\left[−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}\right] \\ $$$${y}_{{A}} =\frac{\mathrm{1}}{\mathrm{2}{m}^{\mathrm{2}} }\left[\mathrm{1}+{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)−\sqrt{\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}\right] \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×{BC}={MA} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({x}_{{B}} −{x}_{{C}} \right)={y}_{{M}} −{y}_{{A}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{{m}^{\mathrm{2}} +\mathrm{4}{h}}=\frac{\mathrm{1}}{\mathrm{2}}\left[{m}^{\mathrm{2}} +\mathrm{2}{h}−\frac{\mathrm{1}}{{m}^{\mathrm{2}} }−{m}^{\mathrm{2}} −\mathrm{2}{h}−\mathrm{1}+\frac{\mathrm{1}}{{m}}\sqrt{\frac{\mathrm{1}}{{m}^{\mathrm{2}} }+\mathrm{2}\left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}\right] \\ $$$$\Rightarrow{m}^{\mathrm{2}} \sqrt{\mathrm{3}\left({m}^{\mathrm{2}} +\mathrm{4}{h}\right)}=\sqrt{\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}−\left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{0}\leqslant{m}<\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow{h}\geqslant\mathrm{3} \\ $$$$ \\ $$$$\mathrm{3}{m}^{\mathrm{4}} \left({m}^{\mathrm{2}} +\mathrm{4}{h}\right)=\left[\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)+\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} +{m}^{\mathrm{4}} −\mathrm{2}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}\right] \\ $$$$\mathrm{2}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}\right)}=\mathrm{2}+\mathrm{4}{m}^{\mathrm{2}} +\mathrm{3}{m}^{\mathrm{4}} \left(\mathrm{1}−{m}^{\mathrm{2}} \right)+\mathrm{4}{m}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right){h} \\ $$$$\Rightarrow\mathrm{16}{m}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right)^{\mathrm{2}} {h}^{\mathrm{2}} +\mathrm{8}{m}^{\mathrm{2}} \left\{\left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right)\left(\mathrm{2}+\mathrm{4}{m}^{\mathrm{2}} +\mathrm{3}{m}^{\mathrm{4}} −\mathrm{3}{m}^{\mathrm{6}} \right)−\mathrm{2}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}{h}+\left\{\left(\mathrm{2}+\mathrm{4}{m}^{\mathrm{2}} +\mathrm{3}{m}^{\mathrm{4}} −\mathrm{3}{m}^{\mathrm{6}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{m}^{\mathrm{2}} +\mathrm{2}{m}^{\mathrm{4}} \right)\right\}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{16}\left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right)^{\mathrm{2}} {h}^{\mathrm{2}} +\mathrm{8}\left(\mathrm{9}{m}^{\mathrm{6}} −\mathrm{12}{m}^{\mathrm{4}} −\mathrm{11}{m}^{\mathrm{2}} −\mathrm{6}\right){h}+{m}^{\mathrm{2}} \left(\mathrm{9}{m}^{\mathrm{6}} −\mathrm{18}{m}^{\mathrm{4}} −\mathrm{23}{m}^{\mathrm{2}} −\mathrm{12}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}=\frac{\left(−\mathrm{9}{m}^{\mathrm{6}} +\mathrm{12}{m}^{\mathrm{4}} +\mathrm{11}{m}^{\mathrm{2}} +\mathrm{6}\right)+\sqrt{\left(\mathrm{9}{m}^{\mathrm{6}} −\mathrm{12}{m}^{\mathrm{4}} −\mathrm{11}{m}^{\mathrm{2}} −\mathrm{6}\right)^{\mathrm{2}} −{m}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{9}{m}^{\mathrm{6}} −\mathrm{18}{m}^{\mathrm{4}} −\mathrm{23}{m}^{\mathrm{2}} −\mathrm{12}\right)}}{\mathrm{4}\left(\mathrm{1}−\mathrm{3}{m}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$…\:{i}\:{stop}\:{here}\:,\:{hope}\:{it}'{s}\:{correct},\:{too}\:{hard}\:{to}\:{simplify}\:… \\ $$$$ \\ $$$${s}=\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\left({x}_{{B}} −{x}_{{C}} \right) \\ $$$$\Rightarrow{s}=\sqrt{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left({m}^{\mathrm{2}} +\mathrm{4}{h}\right)} \\ $$$$\Rightarrow{s}\geqslant\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by ajfour last updated on 27/Jun/19
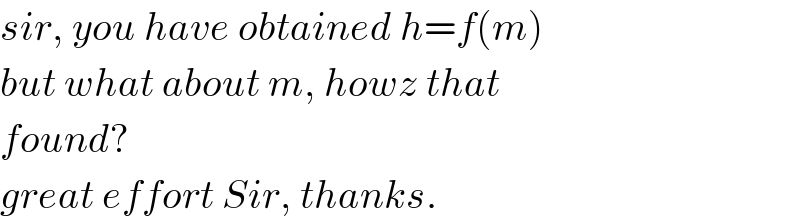
$${sir},\:{you}\:{have}\:{obtained}\:{h}={f}\left({m}\right) \\ $$$${but}\:{what}\:{about}\:{m},\:{howz}\:{that}\: \\ $$$${found}? \\ $$$${great}\:{effort}\:{Sir},\:{thanks}. \\ $$
Commented by mr W last updated on 27/Jun/19

$${i}\:{tried}\:{to}\:{use}\:{m}\:{as}\:{base}\:{parameter}, \\ $$$${then}\:{find}\:{h}\left({m}\right)\:{and}\:{s}\left({m}\right).\:{this}\:{method} \\ $$$${is}\:{easier},\:{since}\:{we}\:{only}\:{need}\:{to}\:{solve} \\ $$$${quadratic}\:{equations}.\:\:{we}\:{find}\:{in}\:{this} \\ $$$${way}:\:{s}\geqslant\mathrm{2}\sqrt{\mathrm{3}}\:{and}\:\mathrm{0}\leqslant{m}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}. \\ $$
Commented by mr W last updated on 27/Jun/19
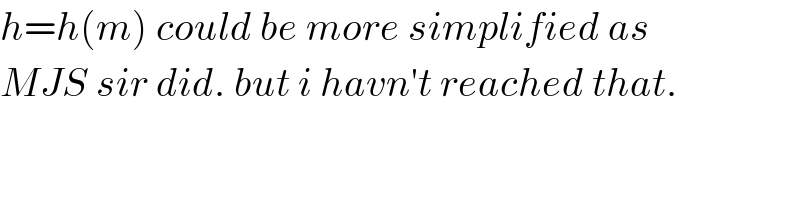
$${h}={h}\left({m}\right)\:{could}\:{be}\:{more}\:{simplified}\:{as} \\ $$$${MJS}\:{sir}\:{did}.\:{but}\:{i}\:{havn}'{t}\:{reached}\:{that}. \\ $$
Answered by MJS last updated on 27/Jun/19

