Menu Close

Question-62895

Tinku Tara 0 Comments
Pin




Question Number 62895 by Tawa1 last updated on 26/Jun/19
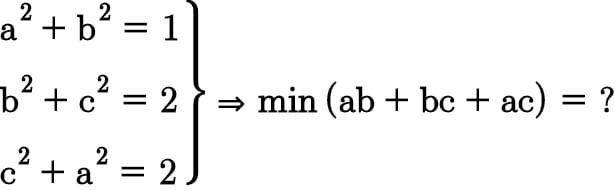
Commented by Tony Lin last updated on 26/Jun/19
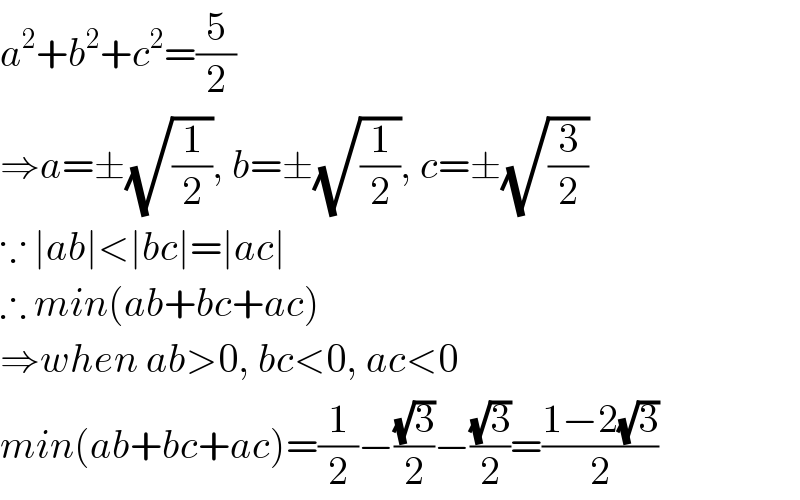
a^2 +b^2 +c^2 =(5/2) ⇒a=±(√(1/2)), b=±(√(1/2)), c=±(√(3/2)) ∵ ∣ab∣<∣bc∣=∣ac∣ ∴ min(ab+bc+ac) ⇒when ab>0, bc<0, ac<0 min(ab+bc+ac)=(1/2)−((√3)/2)−((√3)/2)=((1−2(√3))/2)
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow{a}=\pm\sqrt{\frac{\mathrm{1}}{\mathrm{2}}},\:{b}=\pm\sqrt{\frac{\mathrm{1}}{\mathrm{2}}},\:{c}=\pm\sqrt{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\because\:\mid{ab}\mid<\mid{bc}\mid=\mid{ac}\mid \\ $$$$\therefore\:{min}\left({ab}+{bc}+{ac}\right) \\ $$$$\Rightarrow{when}\:{ab}>\mathrm{0},\:{bc}<\mathrm{0},\:{ac}<\mathrm{0} \\ $$$${min}\left({ab}+{bc}+{ac}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 26/Jun/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Kunal12588 last updated on 26/Jun/19
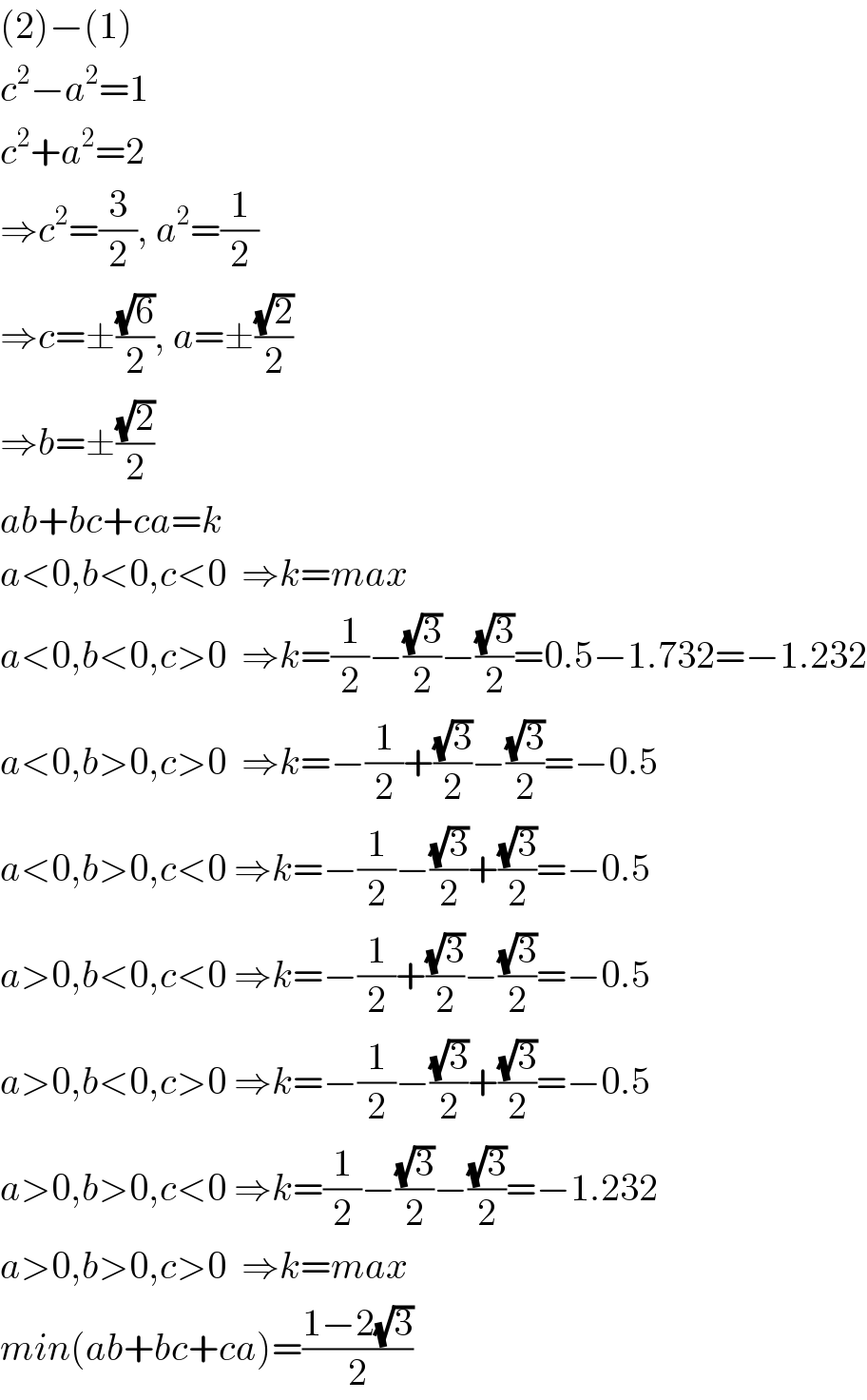
(2)−(1) c^2 −a^2 =1 c^2 +a^2 =2 ⇒c^2 =(3/2), a^2 =(1/2) ⇒c=±((√6)/2), a=±((√2)/2) ⇒b=±((√2)/2) ab+bc+ca=k a<0,b<0,c<0 ⇒k=max a<0,b<0,c>0 ⇒k=(1/2)−((√3)/2)−((√3)/2)=0.5−1.732=−1.232 a<0,b>0,c>0 ⇒k=−(1/2)+((√3)/2)−((√3)/2)=−0.5 a<0,b>0,c<0 ⇒k=−(1/2)−((√3)/2)+((√3)/2)=−0.5 a>0,b<0,c<0 ⇒k=−(1/2)+((√3)/2)−((√3)/2)=−0.5 a>0,b<0,c>0 ⇒k=−(1/2)−((√3)/2)+((√3)/2)=−0.5 a>0,b>0,c<0 ⇒k=(1/2)−((√3)/2)−((√3)/2)=−1.232 a>0,b>0,c>0 ⇒k=max min(ab+bc+ca)=((1−2(√3))/2)
$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right) \\ $$$${c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{1} \\ $$$${c}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}},\:{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{c}=\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{2}},\:{a}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{b}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${ab}+{bc}+{ca}={k} \\ $$$${a}<\mathrm{0},{b}<\mathrm{0},{c}<\mathrm{0}\:\:\Rightarrow{k}={max} \\ $$$${a}<\mathrm{0},{b}<\mathrm{0},{c}>\mathrm{0}\:\:\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{0}.\mathrm{5}−\mathrm{1}.\mathrm{732}=−\mathrm{1}.\mathrm{232} \\ $$$${a}<\mathrm{0},{b}>\mathrm{0},{c}>\mathrm{0}\:\:\Rightarrow{k}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{0}.\mathrm{5} \\ $$$${a}<\mathrm{0},{b}>\mathrm{0},{c}<\mathrm{0}\:\Rightarrow{k}=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{0}.\mathrm{5} \\ $$$${a}>\mathrm{0},{b}<\mathrm{0},{c}<\mathrm{0}\:\Rightarrow{k}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{0}.\mathrm{5} \\ $$$${a}>\mathrm{0},{b}<\mathrm{0},{c}>\mathrm{0}\:\Rightarrow{k}=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{0}.\mathrm{5} \\ $$$${a}>\mathrm{0},{b}>\mathrm{0},{c}<\mathrm{0}\:\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{1}.\mathrm{232} \\ $$$${a}>\mathrm{0},{b}>\mathrm{0},{c}>\mathrm{0}\:\:\Rightarrow{k}={max} \\ $$$${min}\left({ab}+{bc}+{ca}\right)=\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 26/Jun/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *