Question Number 62970 by ajfour last updated on 27/Jun/19

Commented by ajfour last updated on 28/Jun/19
$${Hope}\:{its}\:\:{correct}\:{and}\:{unique}.. \\ $$
Answered by ajfour last updated on 27/Jun/19
Commented by ajfour last updated on 27/Jun/19
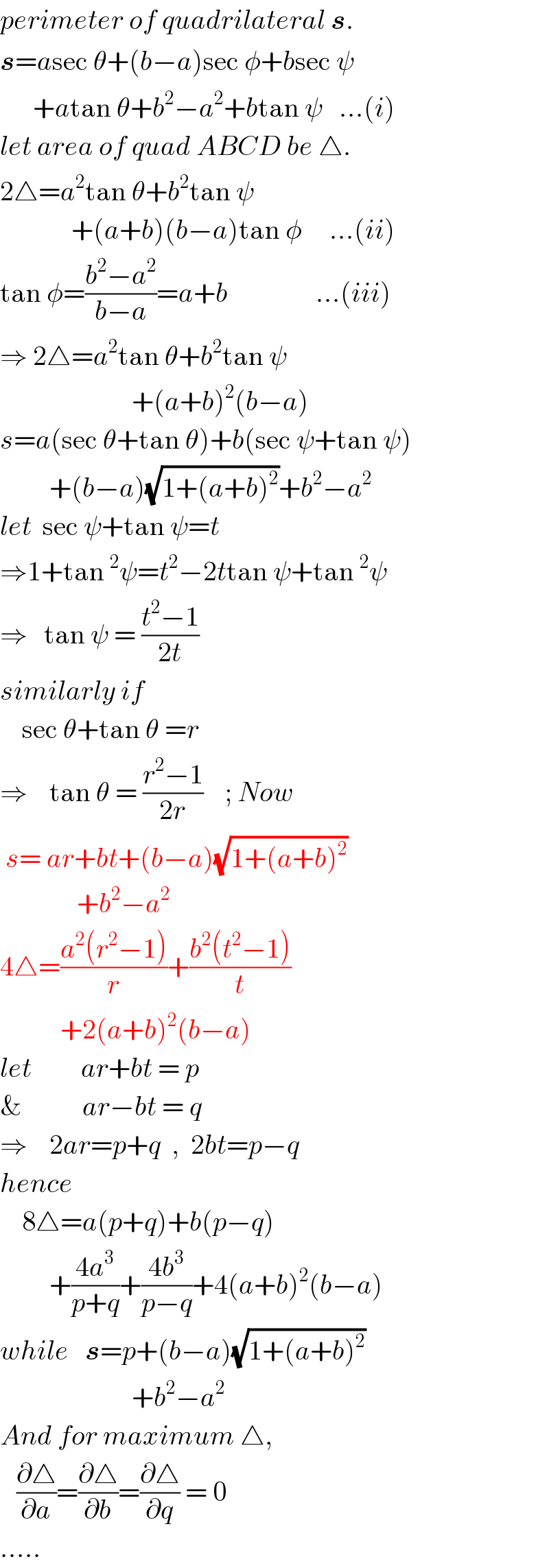
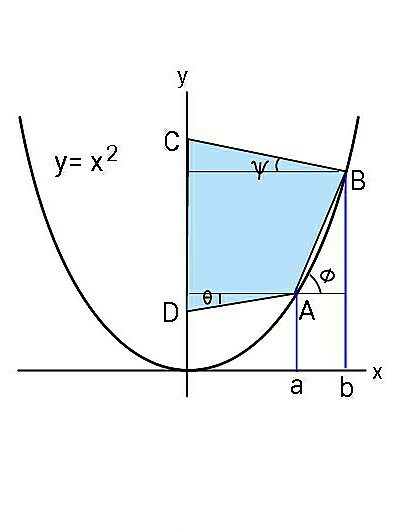
$${perimeter}\:{of}\:{quadrilateral}\:\boldsymbol{{s}}. \\ $$$$\boldsymbol{{s}}={a}\mathrm{sec}\:\theta+\left({b}−{a}\right)\mathrm{sec}\:\phi+{b}\mathrm{sec}\:\psi \\ $$$$\:\:\:\:\:\:+{a}\mathrm{tan}\:\theta+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} +{b}\mathrm{tan}\:\psi\:\:\:…\left({i}\right) \\ $$$${let}\:{area}\:{of}\:{quad}\:{ABCD}\:{be}\:\bigtriangleup. \\ $$$$\mathrm{2}\bigtriangleup={a}^{\mathrm{2}} \mathrm{tan}\:\theta+{b}^{\mathrm{2}} \mathrm{tan}\:\psi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({a}+{b}\right)\left({b}−{a}\right)\mathrm{tan}\:\phi\:\:\:\:\:…\left({ii}\right) \\ $$$$\mathrm{tan}\:\phi=\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{b}−{a}}={a}+{b}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\:\mathrm{2}\bigtriangleup={a}^{\mathrm{2}} \mathrm{tan}\:\theta+{b}^{\mathrm{2}} \mathrm{tan}\:\psi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({a}+{b}\right)^{\mathrm{2}} \left({b}−{a}\right) \\ $$$${s}={a}\left(\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\right)+{b}\left(\mathrm{sec}\:\psi+\mathrm{tan}\:\psi\right) \\ $$$$\:\:\:\:\:\:\:\:\:+\left({b}−{a}\right)\sqrt{\mathrm{1}+\left({a}+{b}\right)^{\mathrm{2}} }+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${let}\:\:\mathrm{sec}\:\psi+\mathrm{tan}\:\psi={t} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \psi={t}^{\mathrm{2}} −\mathrm{2}{t}\mathrm{tan}\:\psi+\mathrm{tan}\:^{\mathrm{2}} \psi \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\psi\:=\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}} \\ $$$${similarly}\:{if}\:\: \\ $$$$\:\:\:\:\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\:={r} \\ $$$$\Rightarrow\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}}\:\:\:\:;\:{Now} \\ $$$$\:{s}=\:{ar}+{bt}+\left({b}−{a}\right)\sqrt{\mathrm{1}+\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\mathrm{4}\bigtriangleup=\frac{{a}^{\mathrm{2}} \left({r}^{\mathrm{2}} −\mathrm{1}\right)}{{r}}+\frac{{b}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left({a}+{b}\right)^{\mathrm{2}} \left({b}−{a}\right) \\ $$$${let}\:\:\:\:\:\:\:\:\:{ar}+{bt}\:=\:{p}\:\: \\ $$$$\&\:\:\:\:\:\:\:\:\:\:\:{ar}−{bt}\:=\:{q} \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}{ar}={p}+{q}\:\:,\:\:\mathrm{2}{bt}={p}−{q} \\ $$$${hence} \\ $$$$\:\:\:\:\mathrm{8}\bigtriangleup={a}\left({p}+{q}\right)+{b}\left({p}−{q}\right) \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{4}{a}^{\mathrm{3}} }{{p}+{q}}+\frac{\mathrm{4}{b}^{\mathrm{3}} }{{p}−{q}}+\mathrm{4}\left({a}+{b}\right)^{\mathrm{2}} \left({b}−{a}\right) \\ $$$${while}\:\:\:\boldsymbol{{s}}={p}+\left({b}−{a}\right)\sqrt{\mathrm{1}+\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \: \\ $$$${And}\:{for}\:{maximum}\:\bigtriangleup, \\ $$$$\:\:\:\frac{\partial\bigtriangleup}{\partial{a}}=\frac{\partial\bigtriangleup}{\partial{b}}=\frac{\partial\bigtriangleup}{\partial{q}}\:=\:\mathrm{0} \\ $$$$….. \\ $$
Commented by ajfour last updated on 28/Jun/19

$${Please}\:{help},\:{couldn}'{t}\:{solve}\:{it}; \\ $$$${could}\:{the}\:{quadrilateral}\:{be} \\ $$$${cyclic}\:{for}\:{maximum}\:{area}, \\ $$$${under}\:{these}\:{conditions},\: \\ $$$${could}\:{one}\:{of}\:{the}\:{vertices}\:{of} \\ $$$${quadrilateral}\:{be}\:{at}\:{origin}? \\ $$$${can}\:{one}\:{side}\:{of}\:{quadrilateral} \\ $$$${be}\:{zero},\:{so}\:{that}\:{it}\:{is}\:{afterall}\:{a} \\ $$$${triangle}\:{then},..? \\ $$
Commented by mr W last updated on 28/Jun/19

$${i}\:{believe}\:{that}\:{the}\:{maximum}\:{quadrilateral} \\ $$$${exists},\:{it}\:{mustn}'{t}\:{be}\:{cyclic}\:.\:{but}\:{the} \\ $$$${solution}\:{must}\:{be}\:{very}\:{hard}. \\ $$$${i}'{d}\:{suggest}\:{to}\:{try}\:{the}\:{case}\:{with}\:{a}\:{triangle} \\ $$$${instead}\:{of}\:{quadrilateral}. \\ $$
