Menu Close

Question-63073

Tinku Tara 0 Comments
Pin




Question Number 63073 by ajfour last updated on 28/Jun/19
Commented by ajfour last updated on 28/Jun/19
Find x_(min) .
$${Find}\:{x}_{{min}} \:. \\ $$
Answered by mr W last updated on 28/Jun/19
Commented by mr W last updated on 28/Jun/19
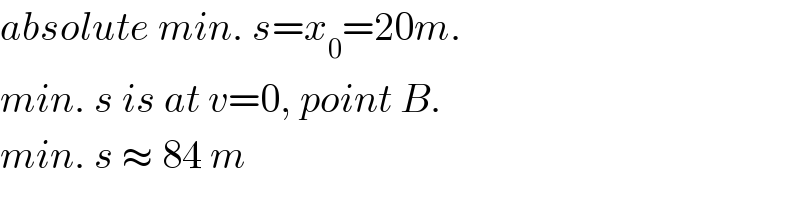
absolute min. s=x_0 =20m. min. s is at v=0, point B. min. s ≈ 84 m
$${absolute}\:{min}.\:{s}={x}_{\mathrm{0}} =\mathrm{20}{m}. \\ $$$${min}.\:{s}\:{is}\:{at}\:{v}=\mathrm{0},\:{point}\:{B}. \\ $$$${min}.\:{s}\:\approx\:\mathrm{84}\:{m} \\ $$
Commented by mr W last updated on 28/Jun/19
Commented by mr W last updated on 28/Jun/19
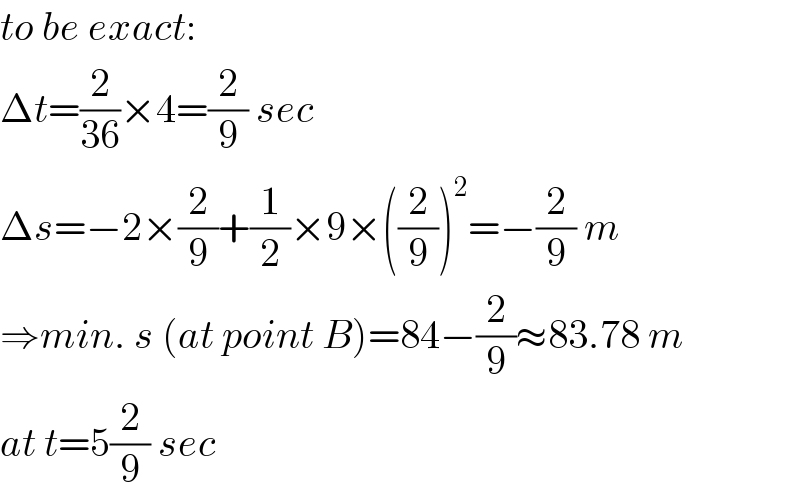
to be exact: Δt=(2/(36))×4=(2/9) sec Δs=−2×(2/9)+(1/2)×9×((2/9))^2 =−(2/9) m ⇒min. s (at point B)=84−(2/9)≈83.78 m at t=5(2/9) sec
$${to}\:{be}\:{exact}: \\ $$$$\Delta{t}=\frac{\mathrm{2}}{\mathrm{36}}×\mathrm{4}=\frac{\mathrm{2}}{\mathrm{9}}\:{sec} \\ $$$$\Delta{s}=−\mathrm{2}×\frac{\mathrm{2}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{9}×\left(\frac{\mathrm{2}}{\mathrm{9}}\right)^{\mathrm{2}} =−\frac{\mathrm{2}}{\mathrm{9}}\:{m} \\ $$$$\Rightarrow{min}.\:{s}\:\left({at}\:{point}\:{B}\right)=\mathrm{84}−\frac{\mathrm{2}}{\mathrm{9}}\approx\mathrm{83}.\mathrm{78}\:{m} \\ $$$${at}\:{t}=\mathrm{5}\frac{\mathrm{2}}{\mathrm{9}}\:{sec} \\ $$
Answered by mr W last updated on 28/Jun/19
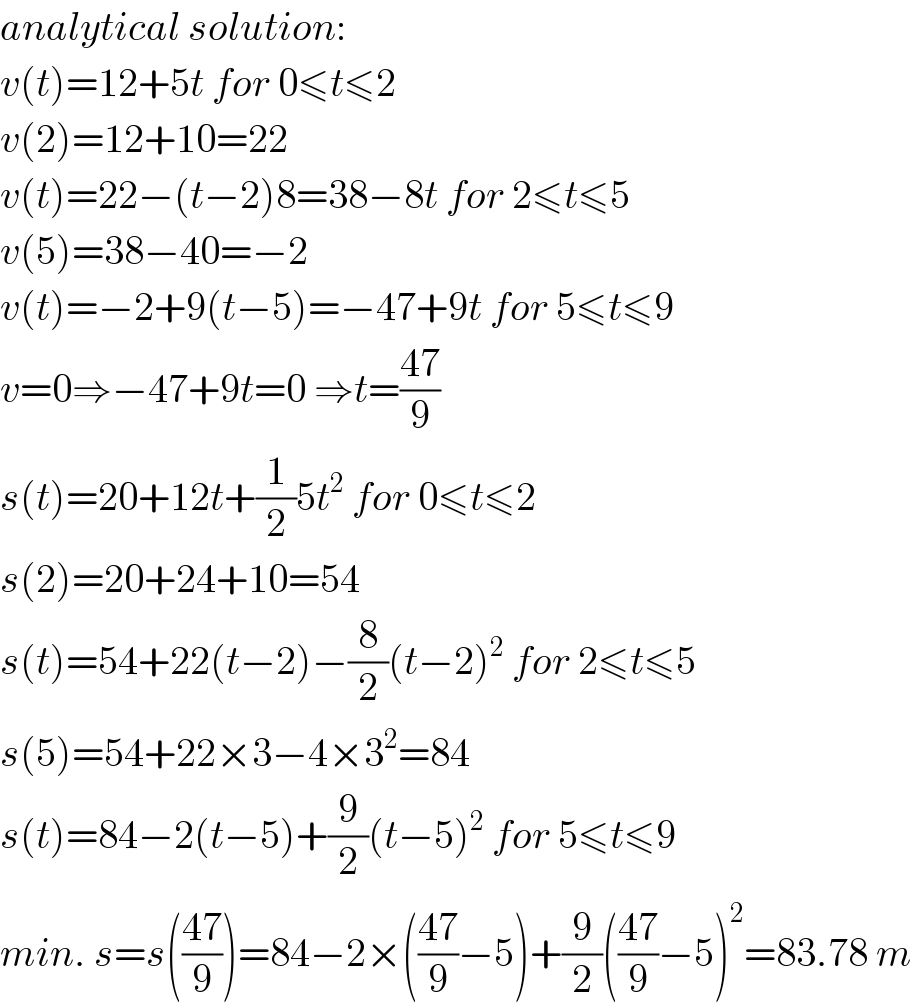
analytical solution: v(t)=12+5t for 0≤t≤2 v(2)=12+10=22 v(t)=22−(t−2)8=38−8t for 2≤t≤5 v(5)=38−40=−2 v(t)=−2+9(t−5)=−47+9t for 5≤t≤9 v=0⇒−47+9t=0 ⇒t=((47)/9) s(t)=20+12t+(1/2)5t^2 for 0≤t≤2 s(2)=20+24+10=54 s(t)=54+22(t−2)−(8/2)(t−2)^2 for 2≤t≤5 s(5)=54+22×3−4×3^2 =84 s(t)=84−2(t−5)+(9/2)(t−5)^2 for 5≤t≤9 min. s=s(((47)/9))=84−2×(((47)/9)−5)+(9/2)(((47)/9)−5)^2 =83.78 m
$${analytical}\:{solution}: \\ $$$${v}\left({t}\right)=\mathrm{12}+\mathrm{5}{t}\:{for}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{2} \\ $$$${v}\left(\mathrm{2}\right)=\mathrm{12}+\mathrm{10}=\mathrm{22} \\ $$$${v}\left({t}\right)=\mathrm{22}−\left({t}−\mathrm{2}\right)\mathrm{8}=\mathrm{38}−\mathrm{8}{t}\:{for}\:\mathrm{2}\leqslant{t}\leqslant\mathrm{5} \\ $$$${v}\left(\mathrm{5}\right)=\mathrm{38}−\mathrm{40}=−\mathrm{2} \\ $$$${v}\left({t}\right)=−\mathrm{2}+\mathrm{9}\left({t}−\mathrm{5}\right)=−\mathrm{47}+\mathrm{9}{t}\:{for}\:\mathrm{5}\leqslant{t}\leqslant\mathrm{9} \\ $$$${v}=\mathrm{0}\Rightarrow−\mathrm{47}+\mathrm{9}{t}=\mathrm{0}\:\Rightarrow{t}=\frac{\mathrm{47}}{\mathrm{9}} \\ $$$${s}\left({t}\right)=\mathrm{20}+\mathrm{12}{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{5}{t}^{\mathrm{2}} \:{for}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{2} \\ $$$${s}\left(\mathrm{2}\right)=\mathrm{20}+\mathrm{24}+\mathrm{10}=\mathrm{54} \\ $$$${s}\left({t}\right)=\mathrm{54}+\mathrm{22}\left({t}−\mathrm{2}\right)−\frac{\mathrm{8}}{\mathrm{2}}\left({t}−\mathrm{2}\right)^{\mathrm{2}} \:{for}\:\mathrm{2}\leqslant{t}\leqslant\mathrm{5} \\ $$$${s}\left(\mathrm{5}\right)=\mathrm{54}+\mathrm{22}×\mathrm{3}−\mathrm{4}×\mathrm{3}^{\mathrm{2}} =\mathrm{84} \\ $$$${s}\left({t}\right)=\mathrm{84}−\mathrm{2}\left({t}−\mathrm{5}\right)+\frac{\mathrm{9}}{\mathrm{2}}\left({t}−\mathrm{5}\right)^{\mathrm{2}} \:{for}\:\mathrm{5}\leqslant{t}\leqslant\mathrm{9} \\ $$$${min}.\:{s}={s}\left(\frac{\mathrm{47}}{\mathrm{9}}\right)=\mathrm{84}−\mathrm{2}×\left(\frac{\mathrm{47}}{\mathrm{9}}−\mathrm{5}\right)+\frac{\mathrm{9}}{\mathrm{2}}\left(\frac{\mathrm{47}}{\mathrm{9}}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{83}.\mathrm{78}\:{m} \\ $$
Commented by mr W last updated on 28/Jun/19
Commented by ajfour last updated on 29/Jun/19
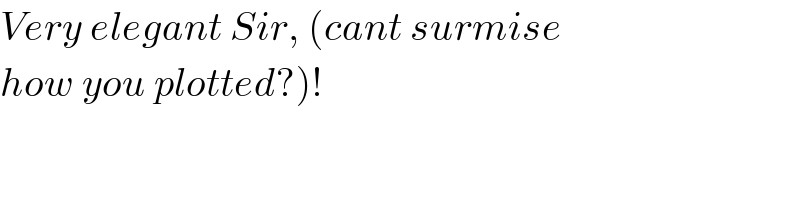
Very elegant Sir, (cant surmise how you plotted?)!
$${Very}\:{elegant}\:{Sir},\:\left({cant}\:{surmise}\right. \\ $$$$\left.{how}\:{you}\:{plotted}?\right)! \\ $$
Commented by mr W last updated on 29/Jun/19
i use the app Grapher for plotting the curves. actually there are three curves. but for each curve you can set its range. this makes them look like a single curve. try it! it′s a good app.
$${i}\:{use}\:{the}\:{app}\:{Grapher}\:{for}\:{plotting} \\ $$$${the}\:{curves}.\:{actually}\:{there}\:{are}\:{three} \\ $$$${curves}.\:{but}\:{for}\:{each}\:{curve}\:{you}\:{can} \\ $$$${set}\:{its}\:{range}.\:{this}\:{makes}\:{them}\:{look} \\ $$$${like}\:{a}\:{single}\:{curve}.\:{try}\:{it}!\:{it}'{s}\:{a}\:{good} \\ $$$${app}. \\ $$
Commented by mr W last updated on 29/Jun/19

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *