Question Number 63108 by ajfour last updated on 29/Jun/19
Commented by ajfour last updated on 29/Jun/19
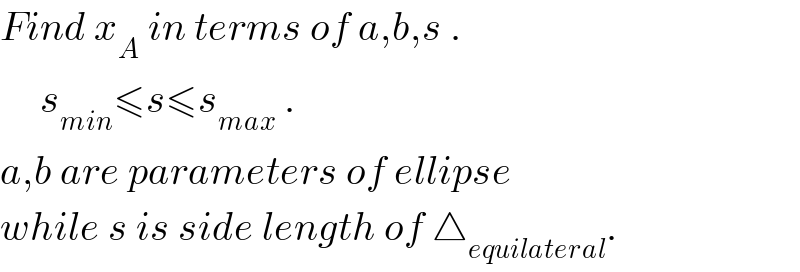
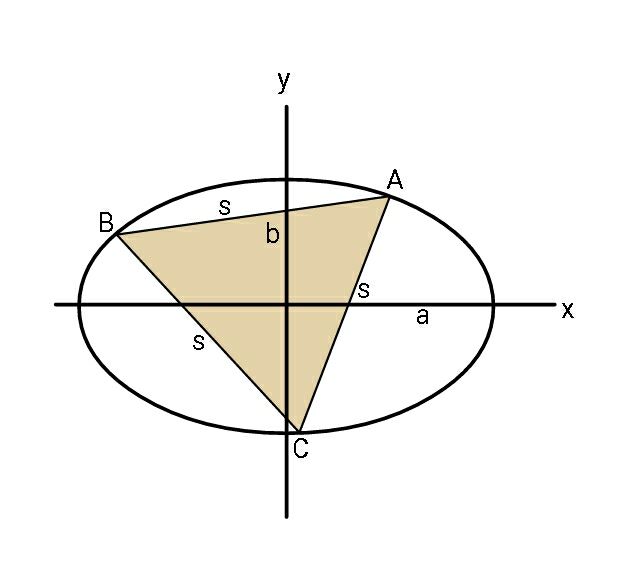
$${Find}\:{x}_{{A}} \:{in}\:{terms}\:{of}\:{a},{b},{s}\:. \\ $$$$\:\:\:\:\:{s}_{{min}} \leqslant{s}\leqslant{s}_{{max}} \:. \\ $$$${a},{b}\:{are}\:{parameters}\:{of}\:{ellipse} \\ $$$${while}\:{s}\:{is}\:{side}\:{length}\:{of}\:\bigtriangleup_{{equilateral}} . \\ $$
Answered by mr W last updated on 02/Jul/19
![R=(s/( (√3)))=radius of circumcircle M(h,k)=centroid and circumcenter let p=(h/a), q=(k/b), α=(R/a)=(s/( (√3)a)), β=(R/b)=(s/( (√3)b)) x_A =h+R cos θ=a((h/a)+(R/a) cos θ)=a(p+α cos θ) y_A =k+R sin θ=b((k/b)+(R/b) sin θ)=b(q+β sin θ) (x_A ^2 /a^2 )+(y_A ^2 /b^2 )=1 ⇒(p+α cos θ)^2 +(q+β sin θ)^2 =1 ⇒p^2 +2αp cos θ+α^2 cos^2 θ+q^2 +2βq sin θ+β^2 sin^2 θ=1 ...(i) x_B =a[p+α cos (θ+((2π)/3))] y_B =b[q+β sin (θ+((2π)/3))] ⇒[p+α cos (θ+((2π)/3))]^2 +[q+β sin (θ+((2π)/3))]^2 =1 ⇒[p−(α/2)(cos θ+(√3) sin θ)]^2 +[q−(β/2)(sin θ−(√3)cos θ)]^2 =1 ⇒p^2 −αp (cos θ+(√3) sin θ)+(α^2 /4)(cos θ+(√3) sin θ)^2 +q^2 −βq (sin θ−(√3) cos θ)+(β^2 /4) (sin θ−(√3) cos θ)^2 =1 ...(ii) x_C =a[p+α cos (θ−((2π)/3))] y_C =b[q+β sin (θ−((2π)/3))] ⇒[p+α cos (θ−((2π)/3))]^2 +[q+β sin (θ−((2π)/3))]^2 =1 ⇒[p−(α/2)(cos θ−(√3) sin θ)]^2 +[q−(β/2)(sin θ+(√3)cos θ)]^2 =1 ⇒p^2 −αp (cos θ−(√3) sin θ)+(α^2 /4)(cos θ−(√3) sin θ)^2 +q^2 −βq (sin θ+(√3)cos θ)+(β^2 /4)(sin θ+(√3)cos θ)^2 =1 ...(iii) (i)−(ii): ⇒α(3cos θ+(√3)sin θ)p+(1/4)α^2 (3cos θ+(√3)sin θ)(cos θ−(√3)sin θ)+β(3sin θ−(√3)cos θ)q+(1/4)β^2 (3 sin θ−(√3)cos θ)(sin θ+(√3)cos θ)=0 ⇒4α(3cos θ+(√3)sin θ)p+4β(3sin θ−(√3)cos θ)q=−(α^2 −β^2 )(3cos 2θ−(√3)sin 2θ) ...(I) (i)−(iii): ⇒αp(2cos θ−(√3)sin θ)+(1/4)α^2 (3cos θ−(√3)sin θ)(cos θ+(√3)sin θ)+βq(3sin θ+(√3)cos θ)+(1/4)β^2 (3sin θ+(√3)cos θ)(sin θ−(√3)cos θ)=0 ⇒4α(3cos θ−(√3)sin θ)p+4β(3sin θ+(√3)cos θ)q=−(α^2 −β^2 )(3cos 2θ+(√3)sin 2θ) ...(II)](https://www.tinkutara.com/question/Q63113.png)
$${R}=\frac{{s}}{\:\sqrt{\mathrm{3}}}={radius}\:{of}\:{circumcircle} \\ $$$${M}\left({h},{k}\right)={centroid}\:{and}\:{circumcenter} \\ $$$${let}\:{p}=\frac{{h}}{{a}},\:{q}=\frac{{k}}{{b}},\:\alpha=\frac{{R}}{{a}}=\frac{{s}}{\:\sqrt{\mathrm{3}}{a}},\:\beta=\frac{{R}}{{b}}=\frac{{s}}{\:\sqrt{\mathrm{3}}{b}} \\ $$$${x}_{{A}} ={h}+{R}\:\mathrm{cos}\:\theta={a}\left(\frac{{h}}{{a}}+\frac{{R}}{{a}}\:\mathrm{cos}\:\theta\right)={a}\left({p}+\alpha\:\mathrm{cos}\:\theta\right) \\ $$$${y}_{{A}} ={k}+{R}\:\mathrm{sin}\:\theta={b}\left(\frac{{k}}{{b}}+\frac{{R}}{{b}}\:\mathrm{sin}\:\theta\right)={b}\left({q}+\beta\:\mathrm{sin}\:\theta\right) \\ $$$$\frac{{x}_{{A}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{A}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\left({p}+\alpha\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({q}+\beta\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{p}^{\mathrm{2}} +\mathrm{2}\alpha{p}\:\mathrm{cos}\:\theta+\alpha^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+{q}^{\mathrm{2}} +\mathrm{2}\beta{q}\:\mathrm{sin}\:\theta+\beta^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{1}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${x}_{{B}} ={a}\left[{p}+\alpha\:\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right] \\ $$$${y}_{{B}} ={b}\left[{q}+\beta\:\mathrm{sin}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right] \\ $$$$\Rightarrow\left[{p}+\alpha\:\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right]^{\mathrm{2}} +\left[{q}+\beta\:\mathrm{sin}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left[{p}−\frac{\alpha}{\mathrm{2}}\left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)\right]^{\mathrm{2}} +\left[{q}−\frac{\beta}{\mathrm{2}}\left(\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −\alpha{p}\:\left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)+\frac{\alpha^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{q}^{\mathrm{2}} −\beta{q}\:\left(\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right)+\frac{\beta^{\mathrm{2}} }{\mathrm{4}}\:\left(\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{1}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${x}_{{C}} ={a}\left[{p}+\alpha\:\mathrm{cos}\:\left(\theta−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right] \\ $$$${y}_{{C}} ={b}\left[{q}+\beta\:\mathrm{sin}\:\left(\theta−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right] \\ $$$$\Rightarrow\left[{p}+\alpha\:\mathrm{cos}\:\left(\theta−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right]^{\mathrm{2}} +\left[{q}+\beta\:\mathrm{sin}\:\left(\theta−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left[{p}−\frac{\alpha}{\mathrm{2}}\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)\right]^{\mathrm{2}} +\left[{q}−\frac{\beta}{\mathrm{2}}\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −\alpha{p}\:\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)+\frac{\alpha^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{q}^{\mathrm{2}} −\beta{q}\:\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)+\frac{\beta^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{1}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\Rightarrow\alpha\left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right){p}+\frac{\mathrm{1}}{\mathrm{4}}\alpha^{\mathrm{2}} \left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)+\beta\left(\mathrm{3sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right){q}+\frac{\mathrm{1}}{\mathrm{4}}\beta^{\mathrm{2}} \left(\mathrm{3}\:\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\alpha\left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right){p}+\mathrm{4}\beta\left(\mathrm{3sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right){q}=−\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)\left(\mathrm{3cos}\:\mathrm{2}\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)\:\:\:\:\:…\left({I}\right) \\ $$$$\left({i}\right)−\left({iii}\right): \\ $$$$\Rightarrow\alpha{p}\left(\mathrm{2cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)+\frac{\mathrm{1}}{\mathrm{4}}\alpha^{\mathrm{2}} \left(\mathrm{3cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)+\beta{q}\left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)+\frac{\mathrm{1}}{\mathrm{4}}\beta^{\mathrm{2}} \left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\left(\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\alpha\left(\mathrm{3cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right){p}+\mathrm{4}\beta\left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right){q}=−\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)\left(\mathrm{3cos}\:\mathrm{2}\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)\:\:\:\:\:…\left({II}\right) \\ $$
Commented by mr W last updated on 06/Jul/19
![(3cos θ+(√3)sin θ)αp+(3sin θ−(√3)cos θ)βq=−((α^2 −β^2 )/4)(3cos 2θ−(√3)sin 2θ) ...(i) (3cos θ−(√3)sin θ)αp+(3sin θ+(√3)cos θ)βq=−((α^2 −β^2 )/4)(3cos 2θ+(√3)sin 2θ) ...(ii) D=(3cos θ+(√3)sin θ)(3sin θ+(√3)cos θ)−(3cos θ−(√3)sin θ)(3sin θ−(√3)cos θ) =(6sin 2θ+3(√3))−(6sin 2θ−3(√3)) =6(√3) −(4/(α^2 −β^2 ))(αp)D=−(3sin θ−(√3)cos θ)(3cos 2θ+(√3)sin 2θ)+(3sin θ+(√3)cos θ)(3cos 2θ−(√3)sin 2θ) =6(√3)(cos θcos 2θ−sin θsin 2θ) =6(√3)cos 3θ ⇒αp=−((α^2 −β^2 )/4)cos 3θ −(4/(α^2 −β^2 ))(βq)D=−(3cos θ−(√3)sin θ)(3cos 2θ−(√3)sin 2θ)+(3cos θ+(√3)sin θ)(3cos 2θ+(√3)sin 2θ) =6(√3)(sin θcos 2θ+cos θsin 2θ) =6(√3)sin 3θ ⇒βq=−((α^2 −β^2 )/4)sin 3θ put them into (p+α cos θ)^2 +(q+β sin θ)^2 =1 we get b^2 (cos θ+((a^2 −b^2 )/(4b^2 ))cos 3θ)^2 +a^2 (sin θ+((a^2 −b^2 )/(4a^2 ))sin 3θ)^2 =((3a^2 b^2 )/s^2 ) b^2 cos^2 θ[1+(((a^2 −b^2 ))/b^2 )(cos^2 θ−(3/4))]^2 +a^2 sin^2 θ[1+(((a^2 −b^2 ))/a^2 )((3/4)−sin^2 θ)]^2 =((3a^2 b^2 )/s^2 ) b^2 (cos^2 θ−(1/2)+(1/2))[1+(((a^2 −b^2 ))/b^2 )(cos^2 θ−(1/2)−(1/4))]^2 +a^2 ((1/2)−cos^2 θ+(1/2))[1+(((a^2 −b^2 ))/a^2 )(cos^2 θ−(1/2)+(1/4))]^2 =((3a^2 b^2 )/s^2 ) let Φ=cos^2 θ−(1/2) b^2 (Φ+(1/2))[1+(((a^2 −b^2 ))/b^2 )(Φ−(1/4))]^2 +a^2 ((1/2)−Φ)[1+(((a^2 −b^2 ))/a^2 )(Φ+(1/4))]^2 =((3a^2 b^2 )/s^2 ) a^2 (2Φ+1)[4b^2 +(a^2 −b^2 )(4Φ−1)]^2 +b^2 (1−2Φ)[4a^2 +(a^2 −b^2 )(4Φ+1)]^2 =((96a^4 b^4 )/s^2 ) 32(a^2 −b^2 )^3 Φ^3 −6(a^2 −b^2 )^3 Φ+(a^2 +b^2 )[(a^2 +b^2 )^2 +12a^2 b^2 ]−((96a^4 b^4 )/s^2 )=0 [(a^2 −b^2 )Φ]^3 −(3/(16))(a^2 −b^2 )^2 [(a^2 −b^2 )Φ]+{(1/(32))(a^2 +b^2 )[(a^2 +b^2 )^2 +12a^2 b^2 ]−((3a^4 b^4 )/s^2 )}=0 with μ=(b/a)<1, ξ=(s/a) [(1−μ^2 )Φ]^3 −(3/(16))(1−μ^2 )^2 [(1−μ^2 )Φ]+{(1/(32))(1+μ^2 )[(1+μ^2 )^2 +12μ^2 ]−((3μ^4 )/ξ^2 )}=0 with z=(1−μ^2 )Φ=(1−μ^2 )(cos^2 θ−(1/2)) u=(1/(16))(1−μ^2 )^2 v=(1/(64))(1+μ^2 )[(1+μ^2 )^2 +12μ^2 ]−((3μ^4 )/(2ξ^2 )) ⇒z^3 −3uz+2v=0 Δ=−u^3 +v^2 <0 z=2(√u) sin ((1/3)sin^(−1) (v/( (√u^3 )))+((2nπ)/3)) ⇒θ=cos^(−1) (√((1/2)+((2(√μ))/(1−μ^2 )) sin ((1/3)sin^(−1) (v/( (√u^3 )))+((2nπ)/3))))](https://www.tinkutara.com/question/Q63269.png)
$$\left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\alpha{p}+\left(\mathrm{3sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\beta{q}=−\frac{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{3cos}\:\mathrm{2}\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)\:\:\:\:\:…\left({i}\right) \\ $$$$\left(\mathrm{3cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\alpha{p}+\left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\beta{q}=−\frac{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{3cos}\:\mathrm{2}\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)\:\:\:\:\:…\left({ii}\right) \\ $$$${D}=\left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)−\left(\mathrm{3cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{3sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right) \\ $$$$=\left(\mathrm{6sin}\:\mathrm{2}\theta+\mathrm{3}\sqrt{\mathrm{3}}\right)−\left(\mathrm{6sin}\:\mathrm{2}\theta−\mathrm{3}\sqrt{\mathrm{3}}\right) \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$−\frac{\mathrm{4}}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }\left(\alpha{p}\right){D}=−\left(\mathrm{3sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\left(\mathrm{3cos}\:\mathrm{2}\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)+\left(\mathrm{3sin}\:\theta+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)\left(\mathrm{3cos}\:\mathrm{2}\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}}\left(\mathrm{cos}\:\theta\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:\theta\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{3}\theta \\ $$$$\Rightarrow\alpha{p}=−\frac{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }{\mathrm{4}}\mathrm{cos}\:\mathrm{3}\theta \\ $$$$−\frac{\mathrm{4}}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }\left(\beta{q}\right){D}=−\left(\mathrm{3cos}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{3cos}\:\mathrm{2}\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right)+\left(\mathrm{3cos}\:\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)\left(\mathrm{3cos}\:\mathrm{2}\theta+\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}}\left(\mathrm{sin}\:\theta\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:\theta\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$=\mathrm{6}\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{3}\theta \\ $$$$\Rightarrow\beta{q}=−\frac{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }{\mathrm{4}}\mathrm{sin}\:\mathrm{3}\theta \\ $$$${put}\:{them}\:{into}\: \\ $$$$\left({p}+\alpha\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({q}+\beta\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${we}\:{get} \\ $$$${b}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }\mathrm{cos}\:\mathrm{3}\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\mathrm{sin}\:\mathrm{3}\theta\right)^{\mathrm{2}} =\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{s}^{\mathrm{2}} } \\ $$$${b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} }\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{3}}{\mathrm{4}}\right)\right]^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} }\left(\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{sin}^{\mathrm{2}} \:\theta\right)\right]^{\mathrm{2}} =\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{s}^{\mathrm{2}} } \\ $$$${b}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} }\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)\right]^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{cos}^{\mathrm{2}} \:\theta+\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} }\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right]^{\mathrm{2}} =\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{s}^{\mathrm{2}} } \\ $$$${let}\:\Phi=\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \left(\Phi+\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} }\left(\Phi−\frac{\mathrm{1}}{\mathrm{4}}\right)\right]^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\Phi\right)\left[\mathrm{1}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} }\left(\Phi+\frac{\mathrm{1}}{\mathrm{4}}\right)\right]^{\mathrm{2}} =\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{s}^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} \left(\mathrm{2}\Phi+\mathrm{1}\right)\left[\mathrm{4}{b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{4}\Phi−\mathrm{1}\right)\right]^{\mathrm{2}} +{b}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}\Phi\right)\left[\mathrm{4}{a}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{4}\Phi+\mathrm{1}\right)\right]^{\mathrm{2}} =\frac{\mathrm{96}{a}^{\mathrm{4}} {b}^{\mathrm{4}} }{{s}^{\mathrm{2}} } \\ $$$$\mathrm{32}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{3}} \Phi^{\mathrm{3}} −\mathrm{6}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{3}} \Phi+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right]−\frac{\mathrm{96}{a}^{\mathrm{4}} {b}^{\mathrm{4}} }{{s}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left[\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\Phi\right]^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{16}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \left[\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\Phi\right]+\left\{\frac{\mathrm{1}}{\mathrm{32}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right]−\frac{\mathrm{3}{a}^{\mathrm{4}} {b}^{\mathrm{4}} }{{s}^{\mathrm{2}} }\right\}=\mathrm{0} \\ $$$${with}\:\mu=\frac{{b}}{{a}}<\mathrm{1},\:\xi=\frac{{s}}{{a}} \\ $$$$\left[\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\Phi\right]^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{16}}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \left[\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\Phi\right]+\left\{\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\left[\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{12}\mu^{\mathrm{2}} \right]−\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }\right\}=\mathrm{0} \\ $$$${with} \\ $$$${z}=\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\Phi=\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${u}=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${v}=\frac{\mathrm{1}}{\mathrm{64}}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\left[\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{12}\mu^{\mathrm{2}} \right]−\frac{\mathrm{3}\mu^{\mathrm{4}} }{\mathrm{2}\xi^{\mathrm{2}} } \\ $$$$\Rightarrow{z}^{\mathrm{3}} −\mathrm{3}{uz}+\mathrm{2}{v}=\mathrm{0} \\ $$$$\Delta=−{u}^{\mathrm{3}} +{v}^{\mathrm{2}} <\mathrm{0} \\ $$$${z}=\mathrm{2}\sqrt{{u}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{v}}{\:\sqrt{{u}^{\mathrm{3}} }}+\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}\sqrt{\mu}}{\mathrm{1}−\mu^{\mathrm{2}} }\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{v}}{\:\sqrt{{u}^{\mathrm{3}} }}+\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right)} \\ $$
Commented by ajfour last updated on 03/Jul/19
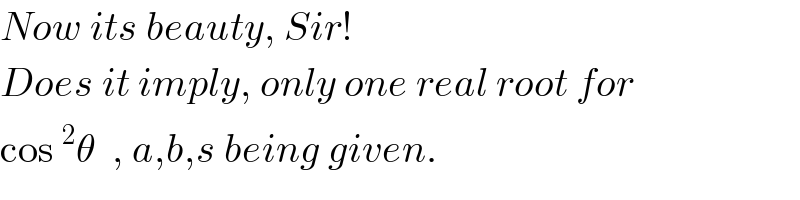
$${Now}\:{its}\:{beauty},\:{Sir}! \\ $$$${Does}\:{it}\:{imply},\:{only}\:{one}\:{real}\:{root}\:{for} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta\:\:,\:{a},{b},{s}\:{being}\:{given}. \\ $$
Commented by ajfour last updated on 02/Jul/19
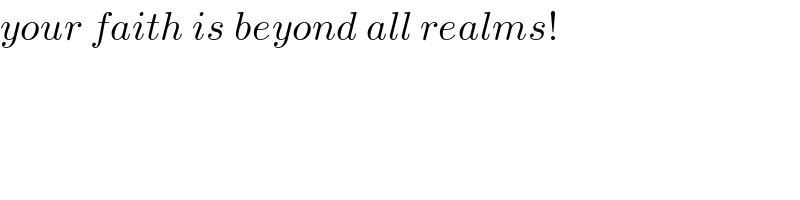
$${your}\:{faith}\:{is}\:{beyond}\:{all}\:{realms}! \\ $$
Commented by ajfour last updated on 02/Jul/19
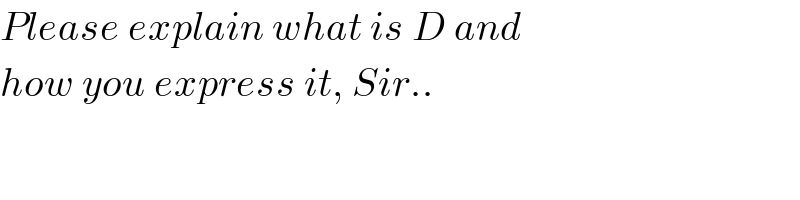
$${Please}\:{explain}\:{what}\:{is}\:{D}\:{and} \\ $$$${how}\:{you}\:{express}\:{it},\:{Sir}.. \\ $$
Commented by mr W last updated on 02/Jul/19

$${thank}\:{you}\:{for}\:{following}\:{sir}! \\ $$$${with}\:{D}\:{i}\:{just}\:{don}'{t}\:{want}\:{to}\:{write} \\ $$$${too}\:{much}\:{when}\:{solving}\:{the}\:{equation} \\ $$$${system}. \\ $$
Commented by mr W last updated on 02/Jul/19

Commented by mr W last updated on 03/Jul/19

$$\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }=\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{3}} \Phi^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{16}}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{3}} \Phi+\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{8}}\mu^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} \right) \\ $$$$\frac{{d}}{{d}\Phi}\left(\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}\Phi^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{16}}=\mathrm{0} \\ $$$$\Rightarrow\Phi=\pm\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\theta=\pm\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{cos}\:\theta=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}},\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{max}.\:{s}\:{or}\:{min}.\:{s}\:{at}\:\theta=\frac{{n}\pi}{\mathrm{2}}\pm\frac{\pi}{\mathrm{6}} \\ $$$${with}\:\Phi=\frac{\mathrm{1}}{\mathrm{4}}: \\ $$$$\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{8}}\mu^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{3}\mu^{\mathrm{2}} }{\xi^{\mathrm{2}} }=\frac{\left(\mathrm{3}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\Rightarrow\xi^{\mathrm{2}} =\frac{\mathrm{48}\mu^{\mathrm{2}} }{\left(\mathrm{3}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\xi_{{max}} =\frac{\mathrm{4}\sqrt{\mathrm{3}}\mu}{\mathrm{3}+\mu^{\mathrm{2}} }=\frac{{s}_{{max}} }{{a}} \\ $$$${with}\:\Phi=−\frac{\mathrm{1}}{\mathrm{4}}: \\ $$$$\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{8}}\mu^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{3}\mu^{\mathrm{4}} }{\xi^{\mathrm{2}} }=\frac{\left(\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\Rightarrow\xi^{\mathrm{2}} =\frac{\mathrm{48}\mu^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\xi_{{min}} =\frac{\mathrm{4}\sqrt{\mathrm{3}}\mu^{\mathrm{2}} }{\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} }=\frac{{s}_{{min}} }{{a}} \\ $$
Answered by ajfour last updated on 06/Jul/19
![let mid-point of BC be M(h,k). slope of AM be m=tan θ x_A =h+((s(√3))/2)cos θ, y_A =k+((s(√3))/2)sin θ x_B =h−(s/2)sin θ , y_B =k+(s/2)cos θ x_C =h+(s/2)sin θ , y_C =k−(s/2)cos θ As B,C lie on ellipse (x_B ^2 /a^2 )+(y_B ^2 /b^2 )=1 , (x_C ^2 /a^2 )+(y_C ^2 /b^2 )=1 subtracting (((x_B −x_C )(x_B +x_C ))/a^2 )+(((y_B −y_C )(y_B +y_C ))/b^2 )=0 ⇒ −2b^2 shsin θ+2a^2 skcos θ=0 ⇒ k=((b^2 h)/a^2 )tan θ similarly as A,B lie on ellipse ⇒ ((b^2 s)/2)((√3)cos θ+sin θ)[2h+(s/2)((√3)cos θ−sin θ)] +((a^2 s)/2)((√3)sin θ−cos θ)[2k+(s/2)((√3)sin θ+cos θ)]=0 ⇒ 2hb^2 ((√3)cos θ+sin θ) +2b^2 h(((sin θ)/(cos θ)))((√3)sin θ−cos θ) +(s/2){b^2 (3cos^2 θ−sin^2 θ)+a^2 (3sin^2 θ−cos^2 θ)}=0 ⇒ h=−((scos θ)/(4(√3)b^2 )){a^2 (3sin^2 θ−cos^2 θ)+b^2 (3cos^2 θ−sin^2 θ)} And as A lies on ellipse, b^2 (h+((s(√3))/2)cos θ)^2 +a^2 (((b^2 h)/a^2 )tan θ+((s(√3))/2)sin θ)^2 =a^2 b^2 ⇒ b^2 h^2 +b^2 sh(√3)cos θ+((3b^2 s^2 cos^2 θ)/4) +((b^4 h^2 tan^2 θ)/a^2 )+b^2 sh(√3)sin θtan θ +((3a^2 s^2 sin^2 θ)/4)=a^2 b^2 ⇒ b^2 h^2 (1+(b^2 /a^2 )tan^2 θ)+((b^2 sh(√3))/(cos θ)) +((3s^2 )/4)(b^2 cos^2 θ+a^2 sin^2 θ)=a^2 b^2 ⇒ (b^2 /a^2 )(a^2 cos^2 θ+b^2 sin^2 θ)(h^2 /(cos^2 θ)) +(b^2 s(√3))(h/(cos θ))+(3/4)s^2 (b^2 cos^2 θ+a^2 sin^2 θ) −a^2 b^2 =0 let cos θ=t , then (b^2 /a^2 )((h/t))^2 {b^2 +(a^2 −b^2 )t^2 }+b^2 s(√3)((h/t)) +((3s^2 )/4)[a^2 −(a^2 −b^2 )t^2 ] −a^2 b^2 = 0 where h=−((scos θ)/(4(√3)b^2 )){a^2 (3sin^2 θ−cos^2 θ)+b^2 (3cos^2 θ−sin^2 θ)} ⇒ (h/t)=−(s/(4(√3)b^2 )){3a^2 −b^2 −4(a^2 −b^2 )t^2 } Now (b^2 /a^2 )((s^2 /(48b^4 ))){b^2 +(a^2 −b^2 )t^2 }{3a^2 −b^2 −4(a^2 −b^2 )t^2 }^2 −b^2 s(√3)((s/(4(√3)b^2 ))){3a^2 −b^2 −4(a^2 −b^2 )t^2 } +((3s^2 )/4)[a^2 −(a^2 −b^2 )t^2 ] −a^2 b^2 = 0 let (a^2 −b^2 )t^2 =v (s^2 /(48a^2 b^2 ))(b^2 +v)(3a^2 −b^2 −4v)^2 +(s^2 /4)(b^2 +v)−a^2 b^2 =0 let b^2 +v= y ⇒ ((s^2 /(48a^2 b^2 )))y{3(a^2 +b^2 )−4y}^2 +((s^2 y)/4)−a^2 b^2 = 0 _________________________ ⇒ s^2 y{[3(a^2 +b^2 )−4y]^2 +12a^2 b^2 } −48a^4 b^4 =0 _________________________](https://www.tinkutara.com/question/Q63132.png)
$${let}\:{mid}-{point}\:{of}\:{BC}\:{be}\:{M}\left({h},{k}\right). \\ $$$${slope}\:{of}\:{AM}\:{be}\:{m}=\mathrm{tan}\:\theta \\ $$$${x}_{{A}} ={h}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\theta,\:\:\:{y}_{{A}} ={k}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$${x}_{{B}} ={h}−\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\theta\:\:,\:\:{y}_{{B}} ={k}+\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\theta \\ $$$${x}_{{C}} ={h}+\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\theta\:\:,\:\:{y}_{{C}} ={k}−\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\theta \\ $$$${As}\:{B},{C}\:\:{lie}\:{on}\:{ellipse} \\ $$$$\:\:\:\:\frac{{x}_{{B}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{B}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:,\:\:\frac{{x}_{{C}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{C}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${subtracting} \\ $$$$\frac{\left({x}_{{B}} −{x}_{{C}} \right)\left({x}_{{B}} +{x}_{{C}} \right)}{{a}^{\mathrm{2}} }+\frac{\left({y}_{{B}} −{y}_{{C}} \right)\left({y}_{{B}} +{y}_{{C}} \right)}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:−\mathrm{2}{b}^{\mathrm{2}} {sh}\mathrm{sin}\:\theta+\mathrm{2}{a}^{\mathrm{2}} {sk}\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{k}=\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} }\mathrm{tan}\:\theta \\ $$$${similarly}\:{as}\:{A},{B}\:{lie}\:{on}\:{ellipse} \\ $$$$\Rightarrow\:\frac{{b}^{\mathrm{2}} {s}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\left[\mathrm{2}{h}+\frac{{s}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\right] \\ $$$$\:+\frac{{a}^{\mathrm{2}} {s}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)\left[\mathrm{2}{k}+\frac{{s}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\right]=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{hb}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right) \\ $$$$+\mathrm{2}{b}^{\mathrm{2}} {h}\left(\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right)\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right) \\ $$$$+\frac{{s}}{\mathrm{2}}\left\{{b}^{\mathrm{2}} \left(\mathrm{3cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\right)+{a}^{\mathrm{2}} \left(\mathrm{3sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\right\}=\mathrm{0} \\ $$$$\Rightarrow\:{h}=−\frac{{s}\mathrm{cos}\:\theta}{\mathrm{4}\sqrt{\mathrm{3}}{b}^{\mathrm{2}} }\left\{{a}^{\mathrm{2}} \left(\mathrm{3sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta\right)+{b}^{\mathrm{2}} \left(\mathrm{3cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\right)\right\} \\ $$$${And}\:{as}\:{A}\:{lies}\:{on}\:{ellipse}, \\ $$$$\:\:\:{b}^{\mathrm{2}} \left({h}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} }\mathrm{tan}\:\theta+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\theta\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {h}^{\mathrm{2}} +{b}^{\mathrm{2}} {sh}\sqrt{\mathrm{3}}\mathrm{cos}\:\theta+\frac{\mathrm{3}{b}^{\mathrm{2}} {s}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{4}} \\ $$$$\:\:\:+\frac{{b}^{\mathrm{4}} {h}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta}{{a}^{\mathrm{2}} }+{b}^{\mathrm{2}} {sh}\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\mathrm{tan}\:\theta \\ $$$$\:\:\:+\frac{\mathrm{3}{a}^{\mathrm{2}} {s}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{4}}={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {h}^{\mathrm{2}} \left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{tan}\:^{\mathrm{2}} \theta\right)+\frac{{b}^{\mathrm{2}} {sh}\sqrt{\mathrm{3}}}{\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:+\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}\left({b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left({a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\right)\frac{{h}^{\mathrm{2}} }{\mathrm{cos}\:^{\mathrm{2}} \theta} \\ $$$$\:\:+\left({b}^{\mathrm{2}} {s}\sqrt{\mathrm{3}}\right)\frac{{h}}{\mathrm{cos}\:\theta}+\frac{\mathrm{3}}{\mathrm{4}}{s}^{\mathrm{2}} \left({b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:−{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\:\mathrm{cos}\:\theta={t}\:,\:{then} \\ $$$$\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{h}}{{t}}\right)^{\mathrm{2}} \left\{{b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right\}+{b}^{\mathrm{2}} {s}\sqrt{\mathrm{3}}\left(\frac{{h}}{{t}}\right) \\ $$$$\:\:\:+\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}\left[{a}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right]\:−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${where} \\ $$$$\:{h}=−\frac{{s}\mathrm{cos}\:\theta}{\mathrm{4}\sqrt{\mathrm{3}}{b}^{\mathrm{2}} }\left\{{a}^{\mathrm{2}} \left(\mathrm{3sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta\right)+{b}^{\mathrm{2}} \left(\mathrm{3cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\right)\right\} \\ $$$$\Rightarrow\:\frac{{h}}{{t}}=−\frac{{s}}{\mathrm{4}\sqrt{\mathrm{3}}{b}^{\mathrm{2}} }\left\{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right\} \\ $$$${Now} \\ $$$$\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{s}^{\mathrm{2}} }{\mathrm{48}{b}^{\mathrm{4}} }\right)\left\{{b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right\}\left\{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$\:−{b}^{\mathrm{2}} {s}\sqrt{\mathrm{3}}\left(\frac{{s}}{\mathrm{4}\sqrt{\mathrm{3}}{b}^{\mathrm{2}} }\right)\left\{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right\} \\ $$$$\:\:\:+\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}\left[{a}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} \right]\:−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\:{let}\:\:\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){t}^{\mathrm{2}} ={v} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{48}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} +{v}\right)\left(\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{4}{v}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{s}^{\mathrm{2}} }{\mathrm{4}}\left({b}^{\mathrm{2}} +{v}\right)−{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\:{b}^{\mathrm{2}} +{v}=\:{y} \\ $$$$\Rightarrow\:\left(\frac{{s}^{\mathrm{2}} }{\mathrm{48}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right){y}\left\{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\mathrm{4}{y}\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{s}^{\mathrm{2}} {y}}{\mathrm{4}}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:{s}^{\mathrm{2}} {y}\left\{\left[\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\mathrm{4}{y}\right]^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{48}{a}^{\mathrm{4}} {b}^{\mathrm{4}} =\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$ \\ $$
Commented by mr W last updated on 01/Jul/19
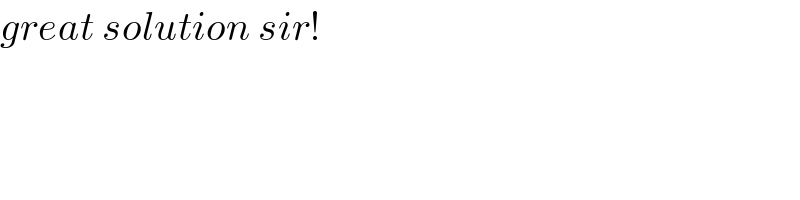
$${great}\:{solution}\:{sir}! \\ $$
Commented by mr W last updated on 03/Jul/19
![sir, please check: s_0 ^2 =((48r^4 a^2 )/((1+r^2 )[(1+r^2 )^2 +3])) ⇒should be min.s s_(min) =((4(√3)b)/(3+((b^2 /a^2 )))) ⇒ should be max. s.](https://www.tinkutara.com/question/Q63370.png)
$${sir},\:{please}\:{check}: \\ $$$${s}_{\mathrm{0}} ^{\mathrm{2}} \:=\frac{\mathrm{48}{r}^{\mathrm{4}} {a}^{\mathrm{2}} }{\left(\mathrm{1}+{r}^{\mathrm{2}} \right)\left[\left(\mathrm{1}+{r}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\right]}\:\Rightarrow{should}\:{be}\:{min}.{s} \\ $$$${s}_{{min}} =\frac{\mathrm{4}\sqrt{\mathrm{3}}{b}}{\mathrm{3}+\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}\:\Rightarrow\:{should}\:{be}\:{max}.\:{s}. \\ $$
Commented by mr W last updated on 03/Jul/19
![an other question is: why (b/a)∈(0,(1/( (√3)))] ? not (b/a)∈(0,1) ? (assume b<a)](https://www.tinkutara.com/question/Q63371.png)
$${an}\:{other}\:{question}\:{is}: \\ $$$${why}\:\frac{{b}}{{a}}\in\left(\mathrm{0},\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]\:?\:{not}\:\frac{{b}}{{a}}\in\left(\mathrm{0},\mathrm{1}\right)\:? \\ $$$$\left({assume}\:{b}<{a}\right) \\ $$
Commented by mr W last updated on 06/Jul/19
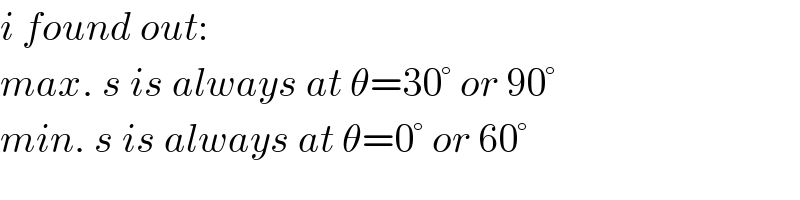
$${i}\:{found}\:{out}:\: \\ $$$${max}.\:{s}\:{is}\:{always}\:{at}\:\theta=\mathrm{30}°\:{or}\:\mathrm{90}° \\ $$$${min}.\:{s}\:{is}\:{always}\:{at}\:\theta=\mathrm{0}°\:{or}\:\mathrm{60}° \\ $$
Commented by mr W last updated on 03/Jul/19

$${with}\:{r}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{something}\:{must}\:{be}\:{wrong}. \\ $$$${in}\:{fact}\:{there}\:{is}\:{solution}\:{for}\:{any} \\ $$$$\mathrm{0}<{r}<\mathrm{1}. \\ $$$${eg}.\:{a}=\mathrm{4},\:{b}=\mathrm{3},\:\Rightarrow{r}=\mathrm{0}.\mathrm{75}>\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}: \\ $$$${at}\:\theta=\mathrm{0}°:\:{s}=\mathrm{5}.\mathrm{8344} \\ $$$${at}\:\theta=\mathrm{30}°:\:{s}=\mathrm{5}.\mathrm{8004} \\ $$$${at}\:\theta=\mathrm{45}°:\:{s}=\mathrm{5}.\mathrm{8172} \\ $$$${with}\:\theta\:{as}\:{meant}\:{in}\:{your}\:{solution}. \\ $$
Commented by mr W last updated on 06/Jul/19
Commented by mr W last updated on 06/Jul/19
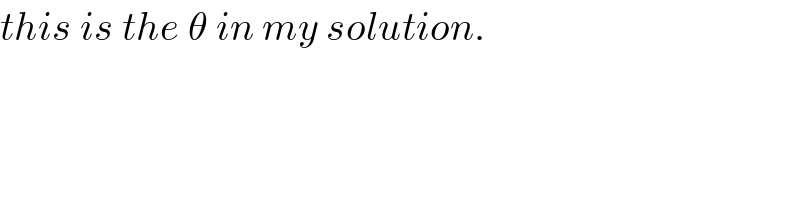
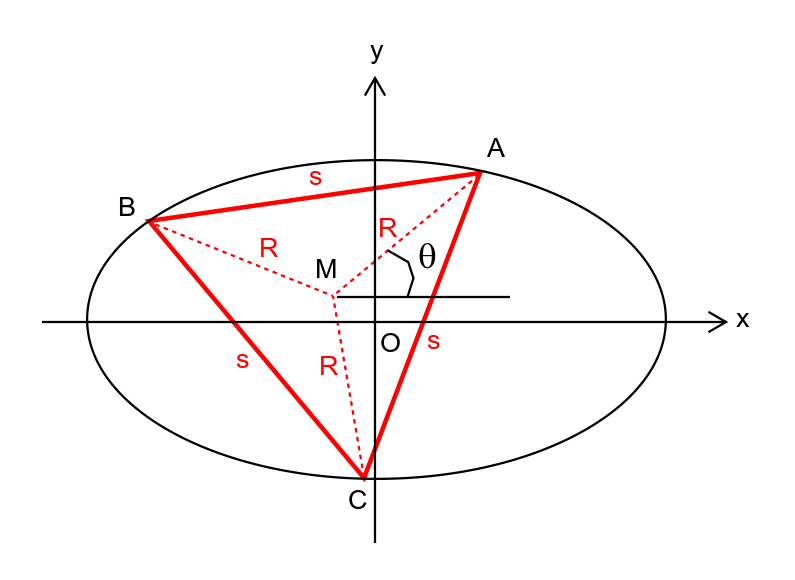
$${this}\:{is}\:{the}\:\theta\:{in}\:{my}\:{solution}. \\ $$
