Question-63206

Question Number 63206 by lalitchand last updated on 30/Jun/19

Commented by lalitchand last updated on 30/Jun/19

$$\mathrm{question}\:\mathrm{number}\:\mathrm{8} \\ $$

Answered by arcana last updated on 01/Jul/19

sea E el punto de interseccion entre los segmentos DB y AC tal que DE^(____) +EB^(____) =DB^(____) ; AE^(___) +EC^(___) =AC^(___) por hipotesis m∠BDC=m∠ACD luego el triangulo △DEC es isosceles ⇒DE^(___) =EC^(___) (1) por otro lado, m∠ACB=m∠ADB (2) y como los angulos ∠DEA, ∠CEB son opuestos por el vertice E entonces ∠DEA≅∠CEB⇒m∠DEA=m∠CEB (3) por (1), (2) y (3), △ADE=△BCE (ALA) ⇒AE^(___) =EB^(___) ⇒DB=DE +EB= AE+EC=AC

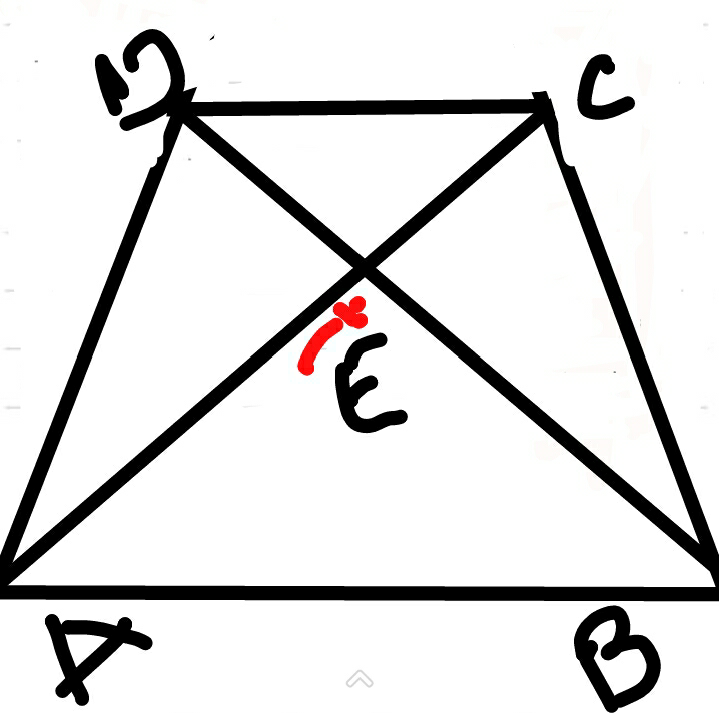
$$\mathrm{sea}\:\mathrm{E}\:\mathrm{el}\:\mathrm{punto}\:\mathrm{de}\:\mathrm{interseccion}\:\mathrm{entre} \\ $$$$\mathrm{los}\:\mathrm{segmentos}\:\mathrm{DB}\:\mathrm{y}\:\mathrm{AC}\:\mathrm{tal}\:\mathrm{que} \\ $$$$\overset{\_\_\_\_} {\mathrm{DE}}\:+\overset{\_\_\_\_} {\mathrm{EB}}=\overset{\_\_\_\_} {\mathrm{DB}}\:;\:\overset{\_\_\_} {\mathrm{AE}}+\overset{\_\_\_} {\mathrm{EC}}=\overset{\_\_\_} {\mathrm{AC}} \\ $$$$ \\ $$$$\mathrm{por}\:\mathrm{hipotesis}\:{m}\angle\mathrm{BDC}={m}\angle\mathrm{ACD} \\ $$$$\mathrm{luego}\:\mathrm{el}\:\mathrm{triangulo}\:\bigtriangleup\mathrm{DEC}\:\mathrm{es}\:\mathrm{isosceles} \\ $$$$\Rightarrow\overset{\_\_\_} {\mathrm{DE}}=\overset{\_\_\_} {\mathrm{EC}}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{por}\:\mathrm{otro}\:\mathrm{lado},\:{m}\angle\mathrm{ACB}={m}\angle\mathrm{ADB}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{y}\:\mathrm{como}\:\mathrm{los}\:\mathrm{angulos}\:\angle\mathrm{DEA},\:\angle\mathrm{CEB} \\ $$$$\mathrm{son}\:\mathrm{opuestos}\:\mathrm{por}\:\mathrm{el}\:\mathrm{vertice}\:\mathrm{E}\:\mathrm{entonces} \\ $$$$\angle\mathrm{DEA}\cong\angle\mathrm{CEB}\Rightarrow{m}\angle\mathrm{DEA}={m}\angle\mathrm{CEB}\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\mathrm{por}\:\left(\mathrm{1}\right),\:\left(\mathrm{2}\right)\:\mathrm{y}\:\left(\mathrm{3}\right),\:\bigtriangleup\mathrm{ADE}=\bigtriangleup\mathrm{BCE}\:\left(\mathrm{ALA}\right) \\ $$$$\Rightarrow\overset{\_\_\_} {\mathrm{AE}}=\overset{\_\_\_} {\mathrm{EB}} \\ $$$$\Rightarrow\mathrm{DB}=\mathrm{DE}\:+\mathrm{EB}=\:\mathrm{AE}+\mathrm{EC}=\mathrm{AC} \\ $$$$ \\ $$

Commented by lalitchand last updated on 01/Jul/19

$$\:\mathrm{Question}\:\mathrm{nmbr}\:\mathrm{8}\:\mathrm{not}\:\mathrm{7} \\ $$

Commented by arcana last updated on 01/Jul/19

$$\mathrm{its}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{question8} \\ $$

Commented by arcana last updated on 01/Jul/19

Commented by lalitchand last updated on 01/Jul/19

$$\mathrm{thanks}\:\mathrm{you}\:\:\mathrm{i}\:\mathrm{understand} \\ $$

Commented by lalitchand last updated on 01/Jul/19

Can you solve 10 number.. i have recently posted

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{10}\:\mathrm{number}..\:\mathrm{i}\:\mathrm{have}\:\mathrm{recently}\: \\ $$$$\mathrm{posted} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply