Question Number 63233 by lalitchand last updated on 01/Jul/19
Commented by lalitchand last updated on 01/Jul/19

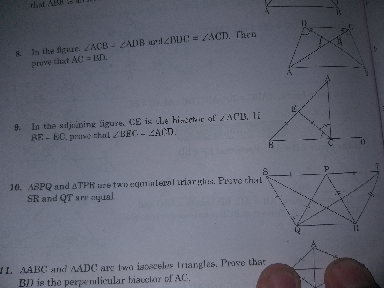
$$\mathrm{question}\:\mathrm{nmbr}\:\mathrm{10} \\ $$
Commented by arcana last updated on 01/Jul/19
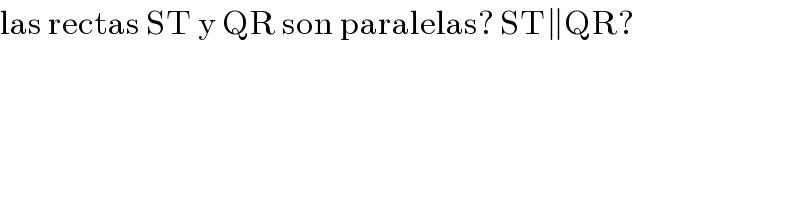
$$\mathrm{las}\:\mathrm{rectas}\:\mathrm{ST}\:\mathrm{y}\:\mathrm{QR}\:\mathrm{son}\:\mathrm{paralelas}?\:\mathrm{ST}\parallel\mathrm{QR}? \\ $$
Commented by arcana last updated on 01/Jul/19

$$\mathrm{si}\:\mathrm{tomamos}\:\mathrm{la}\:\mathrm{bisectriz}\:\mathrm{del}\:\mathrm{vertice}\:\angle\mathrm{SQP} \\ $$$$\mathrm{corta}\:\mathrm{a}\:\mathrm{SP}\:\mathrm{en}\:\mathrm{un}\:\mathrm{punto}\:\mathrm{A}\:\mathrm{de}\:\mathrm{modo}\:\mathrm{que} \\ $$$$\mathrm{m}\angle\mathrm{SQA}=\mathrm{m}\angle\mathrm{AQP}\:\mathrm{pero}\:\mathrm{m}\angle\mathrm{SQP}=\mathrm{60}° \\ $$$$\Rightarrow\mathrm{m}\angle\mathrm{SQA}=\mathrm{m}\angle\mathrm{AQP}=\mathrm{30}° \\ $$$$\mathrm{entonces}\:\mathrm{necesariamente}\:\mathrm{m}\angle\mathrm{QAP}=\mathrm{90}° \\ $$$$\mathrm{ya}\:\mathrm{que}\:\mathrm{m}\angle\mathrm{SPQ}=\mathrm{60}° \\ $$$$\Rightarrow\mathrm{ST}\parallel\mathrm{QR}.\:\mathrm{para}\:\mathrm{que}\:\mathrm{nos}\:\mathrm{sirve}\:\mathrm{esto}? \\ $$$$\mathrm{para}\:\mathrm{usar}\:\mathrm{el}\:\mathrm{teorema}\:\mathrm{de}\:\mathrm{angulos}\:\mathrm{internos} \\ $$$$\mathrm{alternos} \\ $$$$\Rightarrow\mathrm{m}\angle\mathrm{SPQ}=\mathrm{60}°=\mathrm{m}\angle\mathrm{PQR} \\ $$$$ \\ $$$$\mathrm{por}\:\mathrm{otro}\:\mathrm{lado},\:\mathrm{m}\angle\mathrm{SPQ}+\mathrm{m}\angle\mathrm{QPR}+\mathrm{m}\angle\mathrm{RPT}=\mathrm{180}° \\ $$$$\mathrm{60}+\mathrm{m}\angle\mathrm{QPR}+\mathrm{60}=\mathrm{180} \\ $$$$\mathrm{m}\angle\mathrm{QPR}=\mathrm{60} \\ $$$$\mathrm{tambien},\:\mathrm{m}\angle\mathrm{QPR}+\mathrm{m}\angle\mathrm{PQR}+\mathrm{m}\angle\mathrm{PRQ}=\mathrm{180} \\ $$$$\mathrm{60}+\mathrm{60}+\mathrm{m}\angle\mathrm{PRQ}=\mathrm{180} \\ $$
Commented by arcana last updated on 01/Jul/19

$$\mathrm{luego} \\ $$$$\bigtriangleup\mathrm{QPR}\:\mathrm{is}\:\mathrm{equilatero} \\ $$$$\Rightarrow\mathrm{QP}=\mathrm{PR}\Rightarrow\Rightarrow\bigtriangleup\mathrm{SPQ}\cong\bigtriangleup\mathrm{TPR} \\ $$$$\mathrm{ahora},\:\mathrm{una}\:\mathrm{idea}\:\mathrm{es}\:\mathrm{tomar}\:\mathrm{los}\:\mathrm{triangulos} \\ $$$$\bigtriangleup\mathrm{QSR},\:\bigtriangleup\mathrm{RTQ}\:\:\mathrm{y}\:\mathrm{mostrar}\:\mathrm{que}\:\mathrm{sean} \\ $$$$\mathrm{congruentes}\:\mathrm{para}\:\mathrm{tener}\:\mathrm{ST}=\mathrm{QT} \\ $$
