Question Number 63324 by pradyot_pathak last updated on 02/Jul/19

Answered by Hope last updated on 02/Jul/19

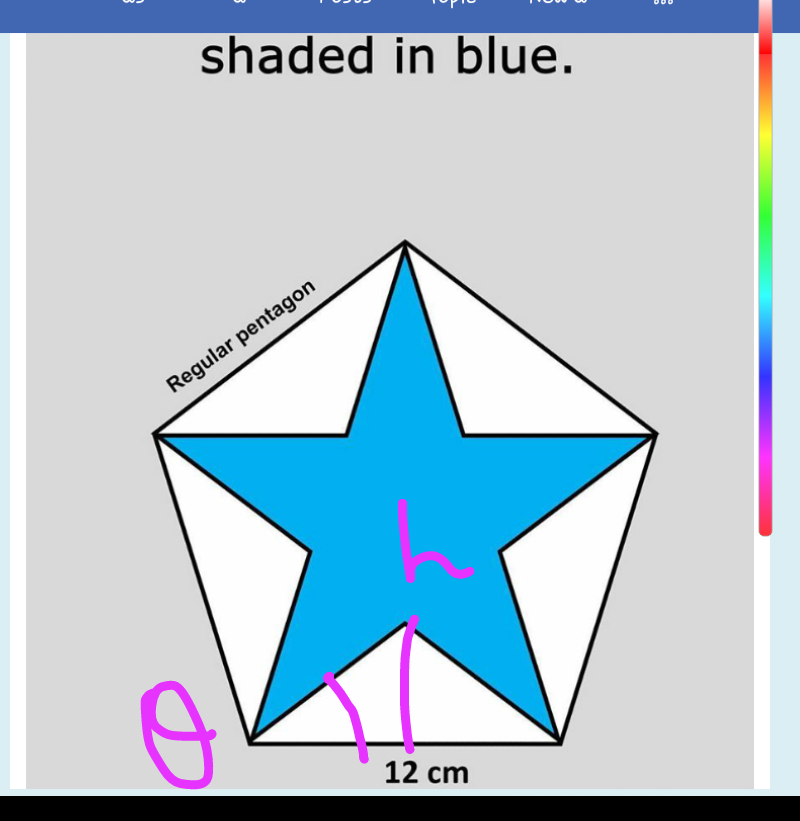
$${area}\:{of}\:{pentagon}=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{5}×\mathrm{12}^{\mathrm{2}} ×{cot}\left(\frac{\mathrm{180}^{{o}} }{\mathrm{5}}\right) \\ $$$$=\mathrm{180}×{cot}\mathrm{36}^{{o}} \\ $$$${external}\:{angle}=\frac{\mathrm{360}^{{o}} }{\mathrm{5}}=\mathrm{72}^{{o}} \\ $$$${internal}\:{angle}=\mathrm{180}^{{o}} −\mathrm{72}^{{o}} =\mathrm{108}^{{o}} \\ $$$$\theta+\theta+\mathrm{108}=\mathrm{180}^{{o}} \rightarrow\theta=\mathrm{36}^{{o}} \\ $$$${area}\:{of}\:{white}\:{triangle}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{12}×{h} \\ $$$${tan}\mathrm{36}^{{o}} =\frac{{h}}{\mathrm{6}}\rightarrow{h}=\mathrm{6}{tan}\mathrm{36}^{{o}} \\ $$$${area}\:{of}\:{five}\left(\mathrm{05}\right){white}\:{triangle}=\mathrm{5}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{12}×\mathrm{6}{tan}\mathrm{36}^{{o}} \\ $$$${area}\:{of}\:{shaded}\:{blue}=\mathrm{180}{cot}\mathrm{36}^{{o}} −\mathrm{180}{tan}\mathrm{36}^{{o}} \\ $$$$=\mathrm{180}\left({cot}\mathrm{36}−{tan}\mathrm{36}\right) \\ $$$$=\mathrm{180}\left(\frac{{cos}^{\mathrm{2}} \mathrm{36}−{sin}^{\mathrm{2}} \mathrm{36}}{{sin}\mathrm{36}{cos}\mathrm{36}}\right) \\ $$$$=\mathrm{360}×\left(\frac{{cos}\mathrm{72}^{{o}} }{{sin}\mathrm{72}^{{o}} }\right) \\ $$$$=\mathrm{360}×{cot}\mathrm{72}^{{o}} \\ $$
Commented by Hope last updated on 02/Jul/19