Menu Close

Question-63351

Tinku Tara 0 Comments
Pin




Question Number 63351 by aliesam last updated on 02/Jul/19
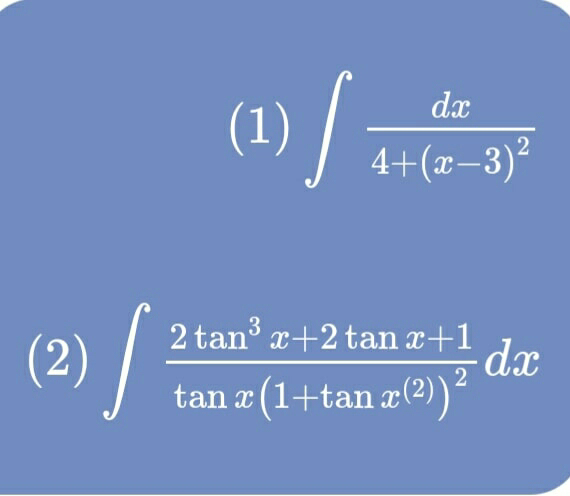
Commented by mathmax by abdo last updated on 03/Jul/19
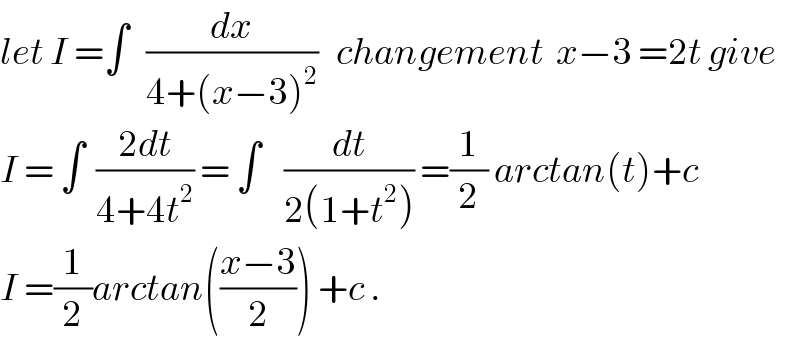
let I =∫ (dx/(4+(x−3)^2 )) changement x−3 =2t give I = ∫ ((2dt)/(4+4t^2 )) = ∫ (dt/(2(1+t^2 ))) =(1/2) arctan(t)+c I =(1/2)arctan(((x−3)/2)) +c .
$${let}\:{I}\:=\int\:\:\:\frac{{dx}}{\mathrm{4}+\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:\:\:{changement}\:\:{x}−\mathrm{3}\:=\mathrm{2}{t}\:{give} \\ $$$${I}\:=\:\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{4}+\mathrm{4}{t}^{\mathrm{2}} }\:=\:\int\:\:\:\:\frac{{dt}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left({t}\right)+{c} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{x}−\mathrm{3}}{\mathrm{2}}\right)\:+{c}\:. \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
let A = ∫ ((2tan^3 x +2tanx +1)/(tanx(1+tan^2 x)^2 )) dx if tan(x)^((2)) means (d^2 /dx^2 )tanx we get tanx^((1)) =1+tan^2 x ⇒tanx^((2)) =2tanx(1+tan^2 x) ⇒ I = ∫ ((2tan^3 x+2tanx +1)/(tanx(1+2tanx(1+tan^2 x))^2 ))dx =∫ ((2tan^3 x +2tanx +1)/(tanx(2tan^3 x +2tanx +1)^2 ))dx = ∫ (dx/(tanx(2tan^3 x +2tanx +1))) changement tanx =t give I = ∫ (1/(t( 2t^(3 ) +2t +1))) (dt/(1+t^2 )) =∫ (dt/(t(1+t^2 )(2t^3 +2t +1))) let decompose F(t) =(1/(t(1+t^2 )(2t^3 +2t +1))) ⇒ F(t) =(a/t) +((bt +c)/(t^2 +1)) +((dt^2 +et +f)/(2t^3 +2t +1)) ⇒ ∫ F(t)dt =∫ ((adt)/t) +∫ ((bt +c)/(t^2 +1)) +∫ ((dt^2 +et +f)/(2t^3 +2t +1)) rest to calculate the coefficient a_i be continued...
$${let}\:{A}\:=\:\int\:\:\frac{\mathrm{2}{tan}^{\mathrm{3}} {x}\:+\mathrm{2}{tanx}\:+\mathrm{1}}{{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:{dx}\:\:\:{if}\:{tan}\left({x}\right)^{\left(\mathrm{2}\right)} \:{means}\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }{tanx}\:{we}\:{get} \\ $$$${tanx}^{\left(\mathrm{1}\right)} \:=\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\Rightarrow{tanx}^{\left(\mathrm{2}\right)} =\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow \\ $$$${I}\:=\:\int\:\:\:\frac{\mathrm{2}{tan}^{\mathrm{3}} {x}+\mathrm{2}{tanx}\:+\mathrm{1}}{{tanx}\left(\mathrm{1}+\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)^{\mathrm{2}} }{dx}\:=\int\:\:\:\frac{\mathrm{2}{tan}^{\mathrm{3}} {x}\:+\mathrm{2}{tanx}\:+\mathrm{1}}{{tanx}\left(\mathrm{2}{tan}^{\mathrm{3}} {x}\:+\mathrm{2}{tanx}\:+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\:\int\:\:\:\:\:\frac{{dx}}{{tanx}\left(\mathrm{2}{tan}^{\mathrm{3}} {x}\:+\mathrm{2}{tanx}\:+\mathrm{1}\right)}\:\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{\mathrm{1}}{{t}\left(\:\mathrm{2}{t}^{\mathrm{3}\:} +\mathrm{2}{t}\:+\mathrm{1}\right)}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\:\:\:\:\frac{{dt}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}\right)} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{dt}^{\mathrm{2}} \:+{et}\:+{f}}{\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\int\:\frac{{adt}}{{t}}\:+\int\:\:\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\int\:\:\:\frac{{dt}^{\mathrm{2}} \:+{et}\:+{f}}{\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}}\:{rest}\:{to}\:{calculate}\:{the}\:{coefficient}\:{a}_{{i}} \\ $$$${be}\:{continued}… \\ $$$$ \\ $$
Answered by Rio Michael last updated on 02/Jul/19
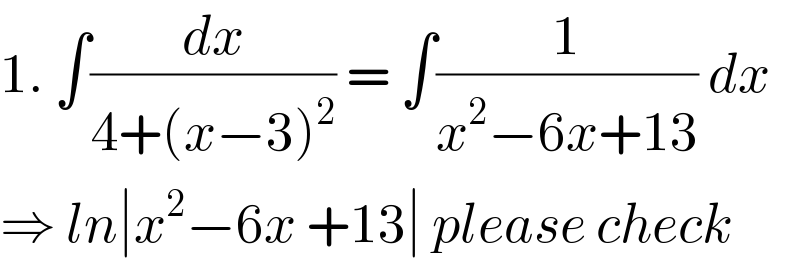
1. ∫(dx/(4+(x−3)^2 )) = ∫(1/(x^2 −6x+13)) dx ⇒ ln∣x^2 −6x +13∣ please check
$$\mathrm{1}.\:\int\frac{{dx}}{\mathrm{4}+\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:=\:\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{13}}\:{dx} \\ $$$$\Rightarrow\:{ln}\mid{x}^{\mathrm{2}} −\mathrm{6}{x}\:+\mathrm{13}\mid\:{please}\:{check} \\ $$
Commented by MJS last updated on 02/Jul/19
(d/dx)[ln (x^2 −6x+13)]=(1/(x^2 −6x+13))×(2x−6) so you′re wrong
$$\frac{{d}}{{dx}}\left[\mathrm{ln}\:\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{13}\right)\right]=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{13}}×\left(\mathrm{2}{x}−\mathrm{6}\right) \\ $$$$\mathrm{so}\:\mathrm{you}'\mathrm{re}\:\mathrm{wrong} \\ $$
Commented by Rio Michael last updated on 04/Jul/19
your right.
$$\:{your}\:{right}. \\ $$
Answered by MJS last updated on 03/Jul/19
∫(dx/(4+(x−3)^2 ))= [t=((x−3)/2) → dx=2dt] =(1/2)∫(dt/(t^2 +1))=(1/2)arctan t =(1/2)arctan ((x−3)/2) +C
$$\int\frac{{dx}}{\mathrm{4}+\left({x}−\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}−\mathrm{3}}{\mathrm{2}}\:\rightarrow\:{dx}=\mathrm{2}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:{t}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{{x}−\mathrm{3}}{\mathrm{2}}\:+{C} \\ $$
Commented by aliesam last updated on 03/Jul/19
god bless you sir
$${god}\:{bless}\:{you}\:{sir} \\ $$
Answered by MJS last updated on 03/Jul/19
the 2^(nd) one cannot be solved with tan (x^2 ) but it′easy like this: ∫((2tan^3 x +2tan x +1)/(tan x (1+tan^2 x)^2 ))dx= [t=tan x → dx=dtcos^2 x] =∫((2t^3 +2t+1)/(t(t^2 +1)^2 ))dt=∫(−(t/((t^2 +1)^2 ))−(t/(t^2 +1))+(2/(t^2 +1))+(1/t))dt= =(1/(2(t^2 +1)))−(1/2)ln (t^2 +1) +2arctan t +ln t ...
$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{with} \\ $$$$\mathrm{tan}\:\left({x}^{\mathrm{2}} \right) \\ $$$$\mathrm{but}\:\mathrm{it}'\mathrm{easy}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\int\frac{\mathrm{2tan}^{\mathrm{3}} \:{x}\:+\mathrm{2tan}\:{x}\:+\mathrm{1}}{\mathrm{tan}\:{x}\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}={dt}\mathrm{cos}^{\mathrm{2}} \:{x}\right] \\ $$$$=\int\frac{\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}=\int\left(−\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{{t}}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\mathrm{2arctan}\:{t}\:+\mathrm{ln}\:{t} \\ $$$$… \\ $$
Commented by aliesam last updated on 03/Jul/19
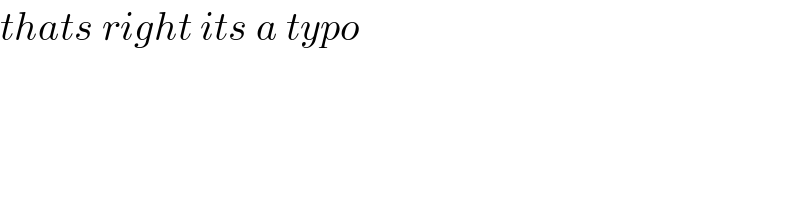
thats right its a typo
$${thats}\:{right}\:{its}\:{a}\:{typo} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *